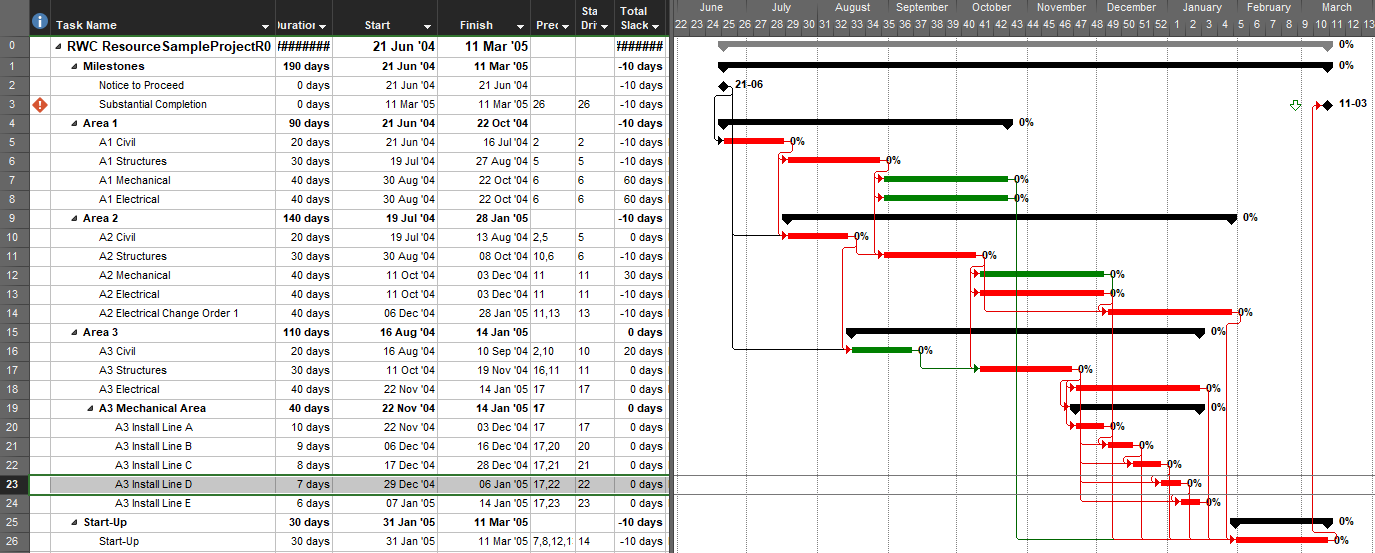
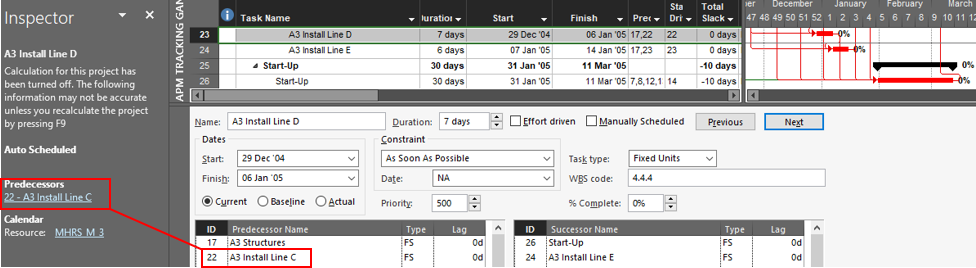
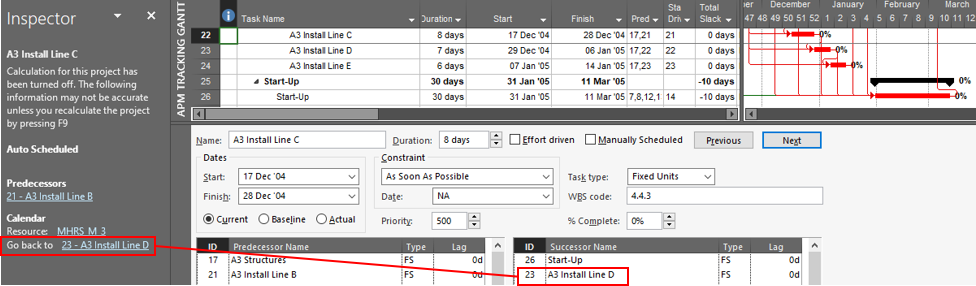
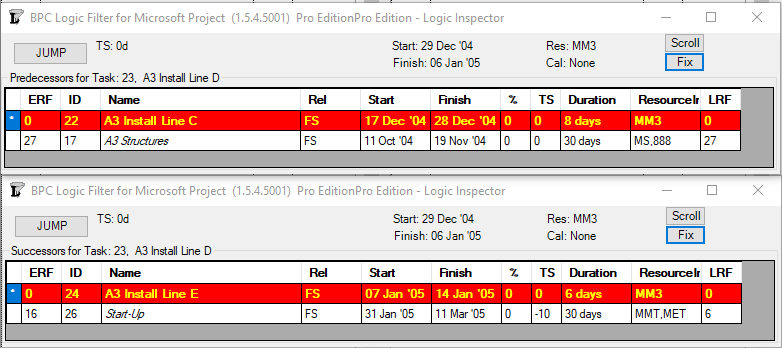
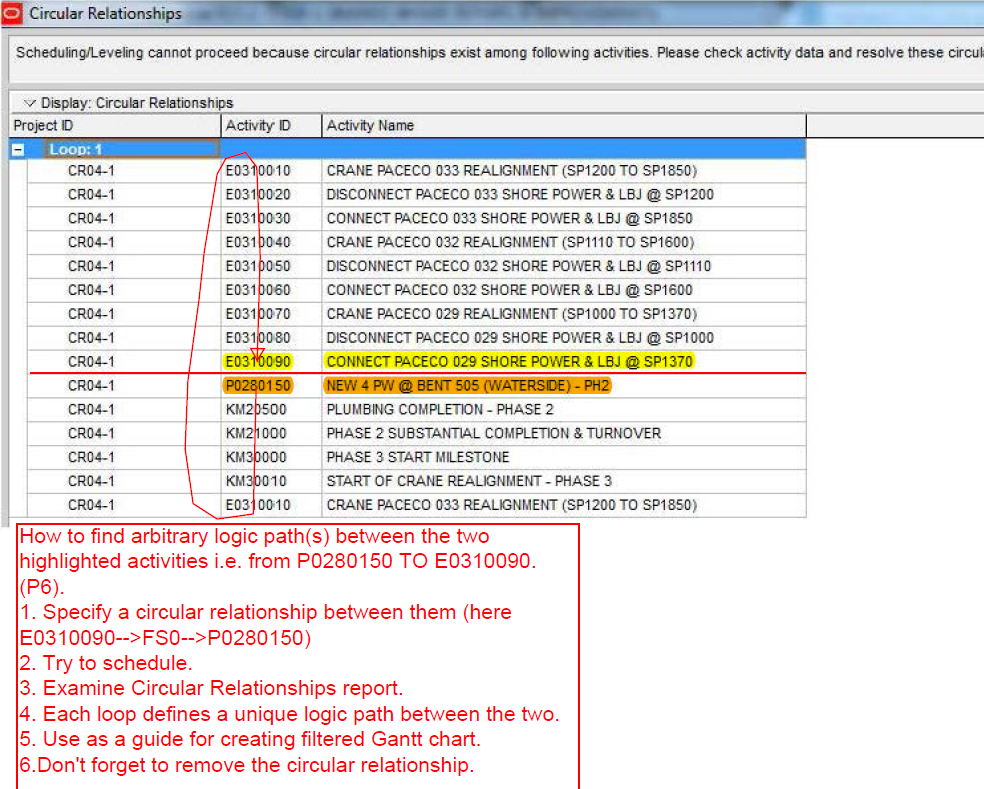
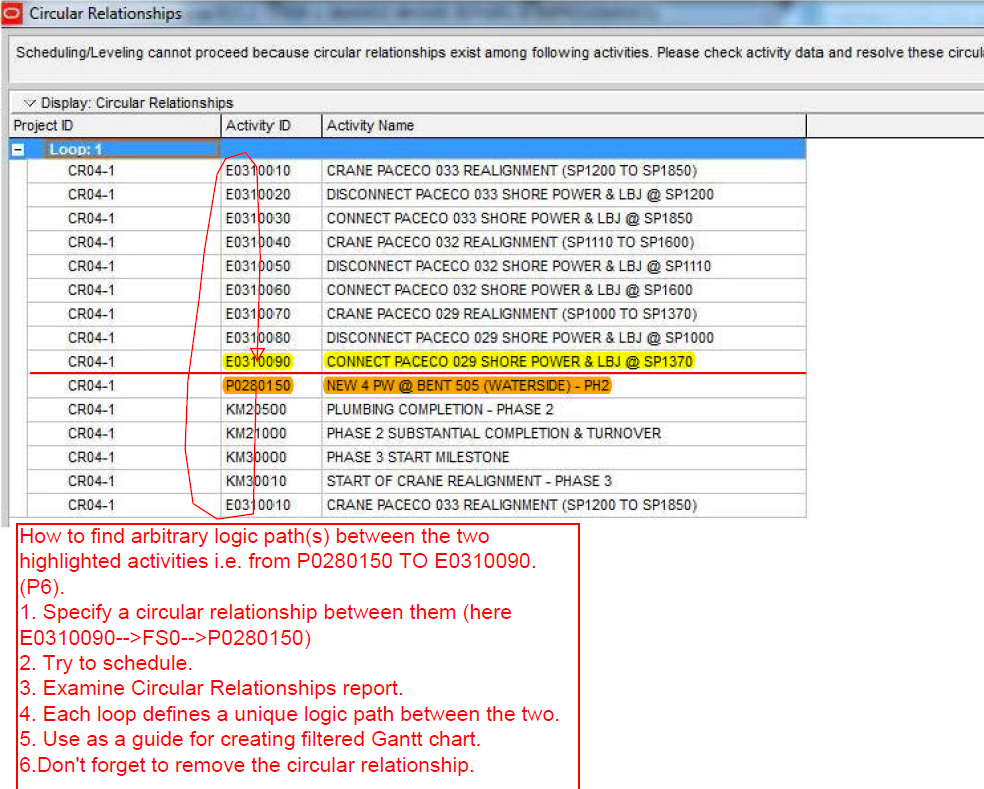
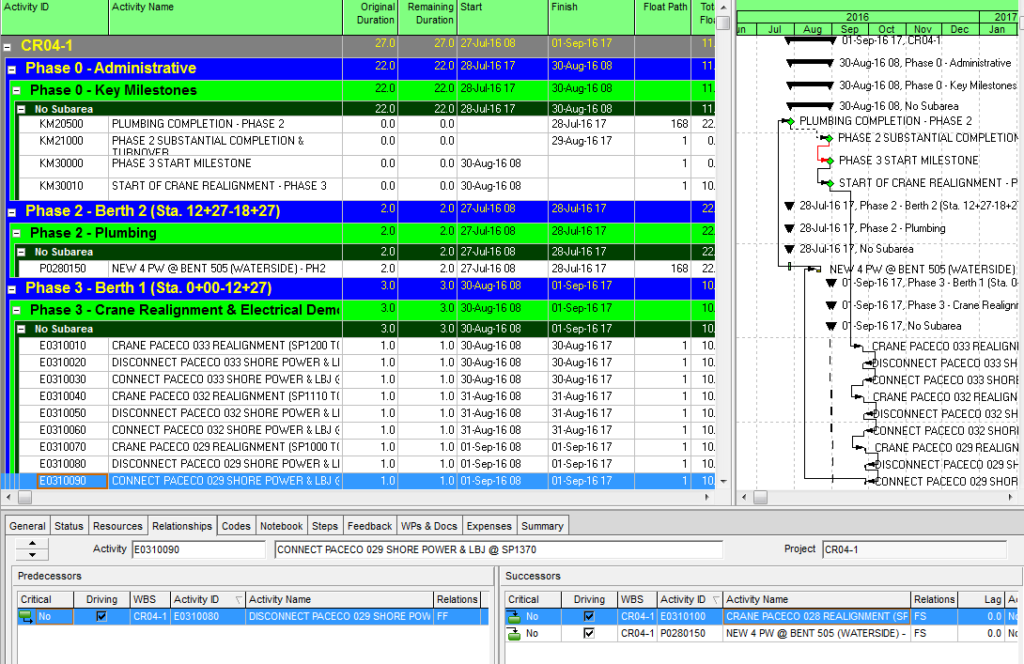
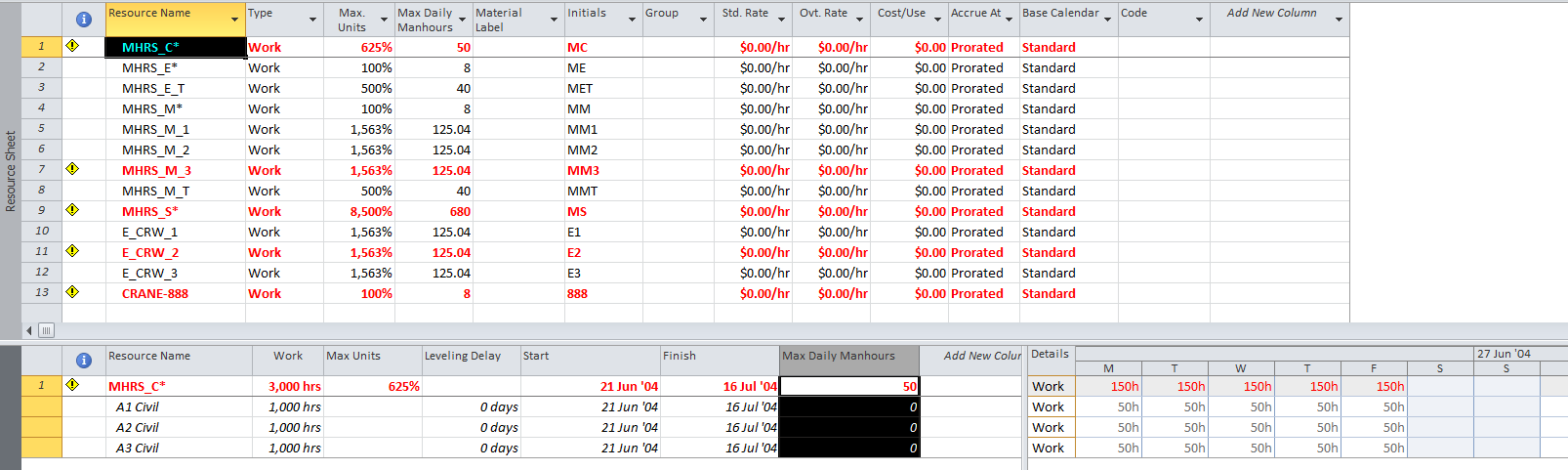
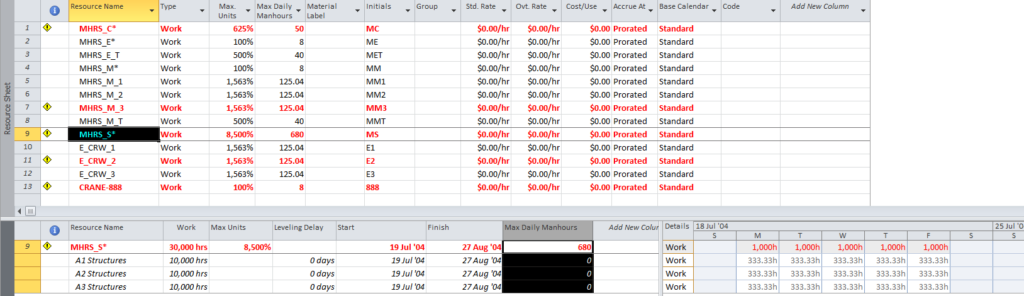
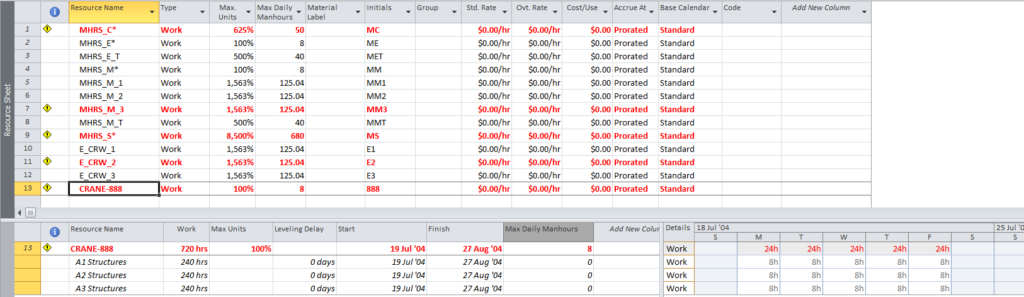
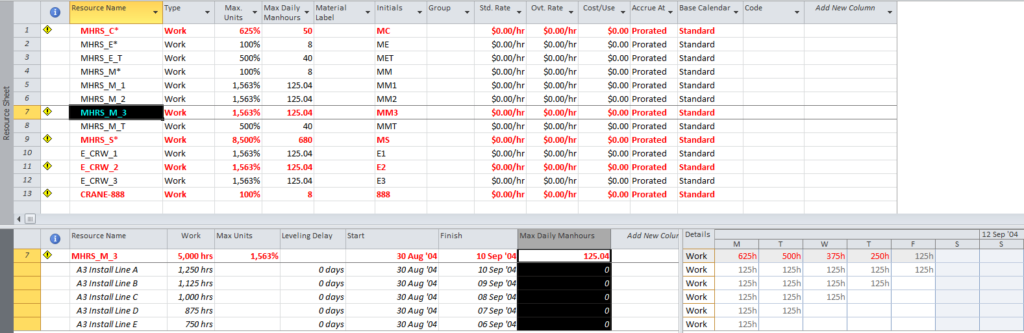
This article highlights the creation of a new targeted report from BPC Logic Filter to identify the “Near Longest Paths” of a project.
While BPC Logic Filter was originally developed as a pure logic tracer, I added a few targeted reports early on to reflect some specific needs, including the “Longest Path Filter” and the “Local Network Filter.” This article highlights the creation of a new targeted report to identify the “Near Longest Paths” of a project.
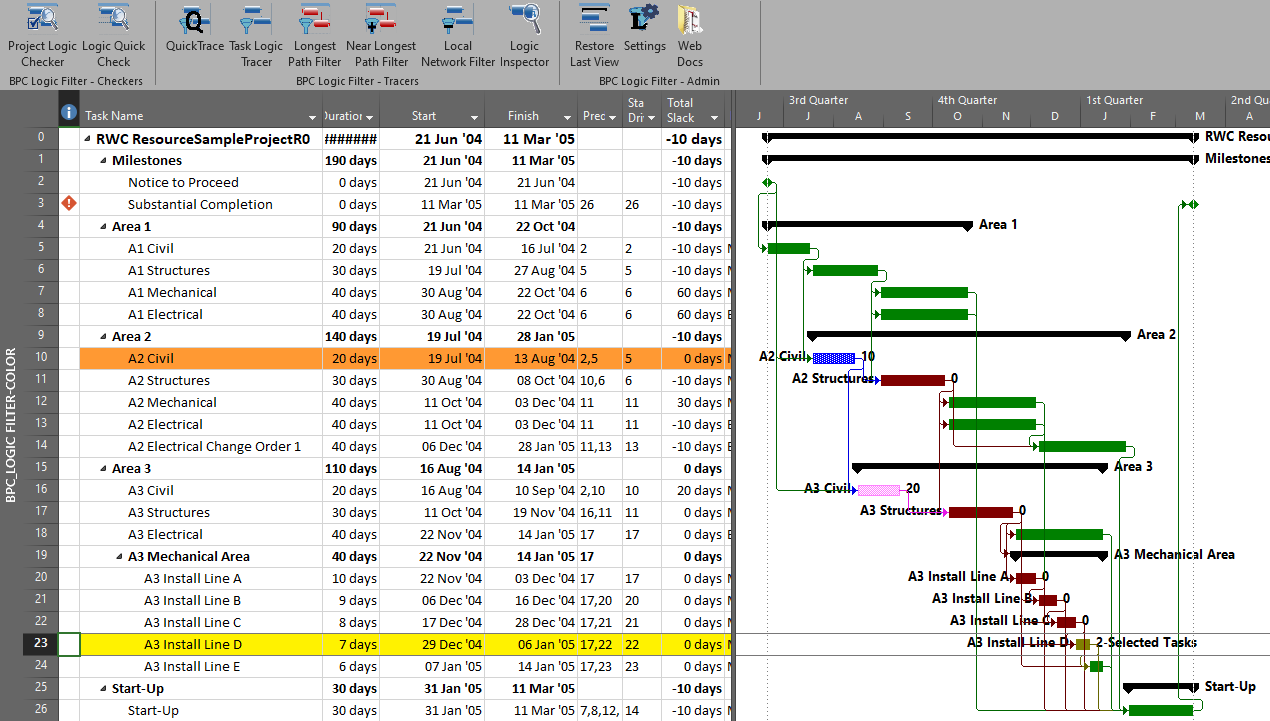
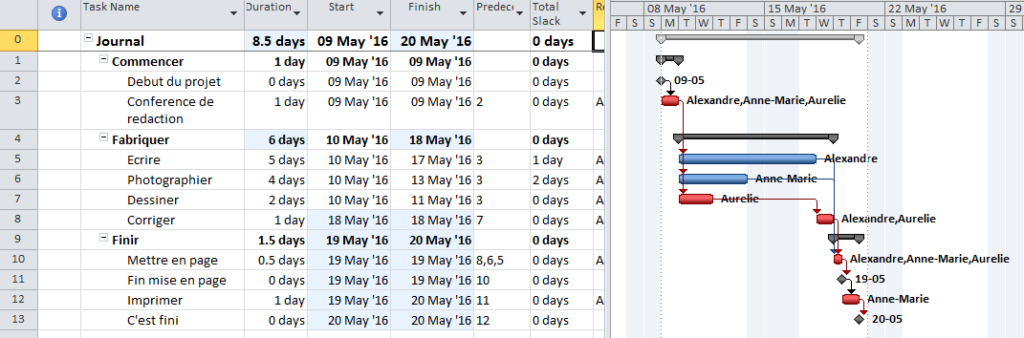
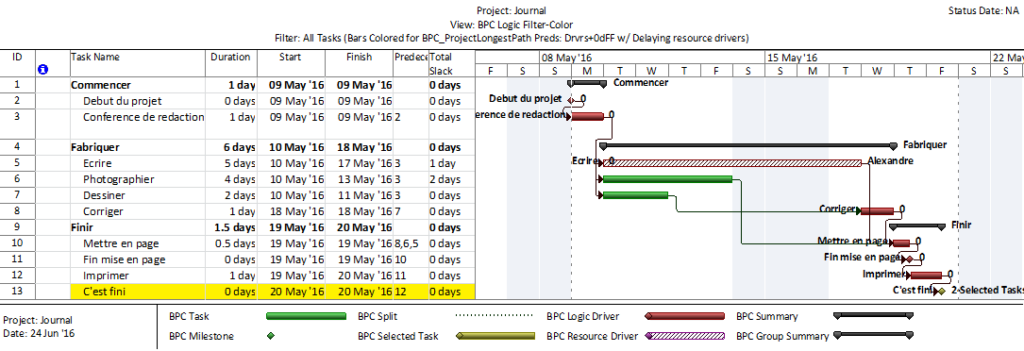
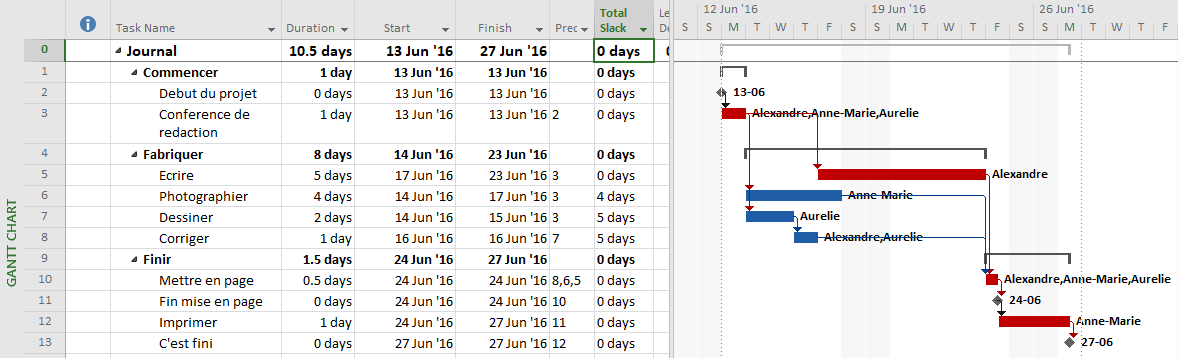
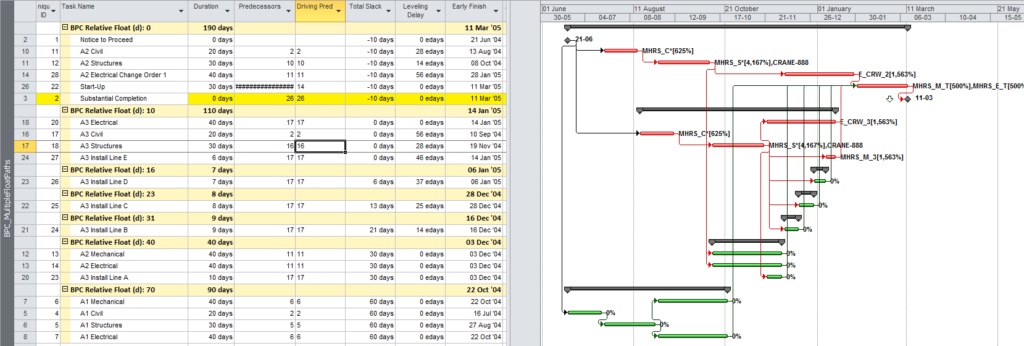
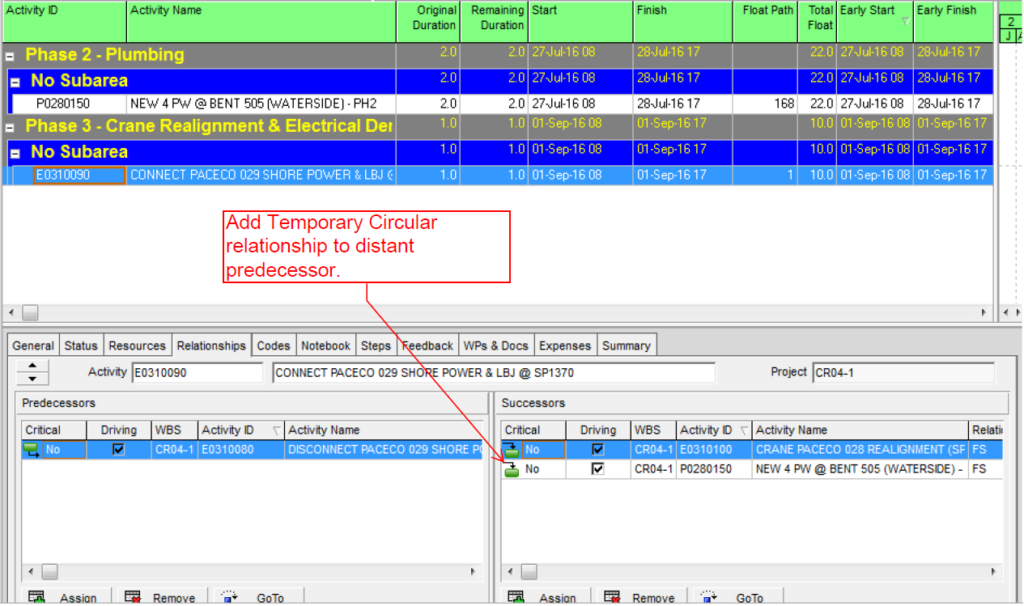
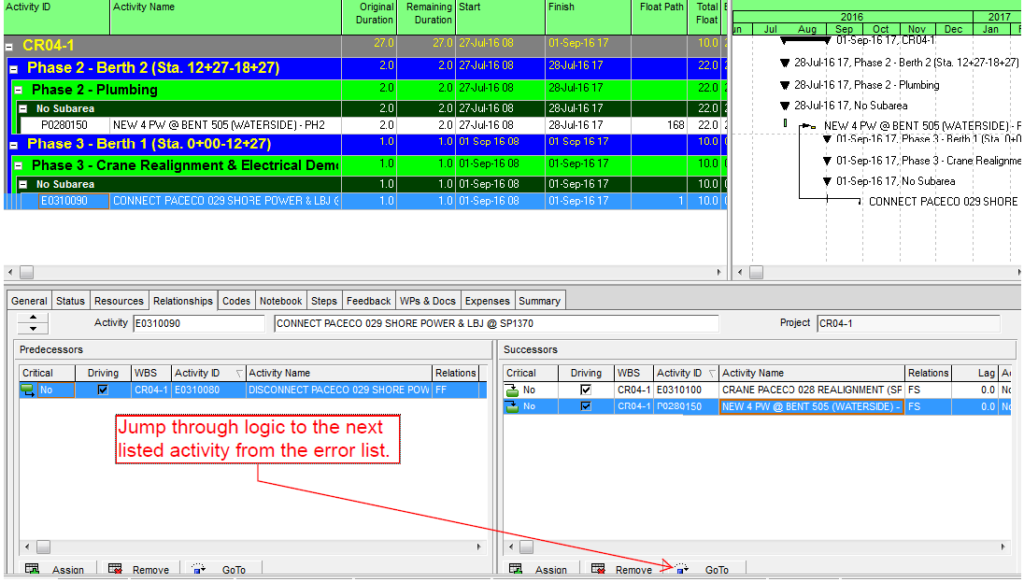
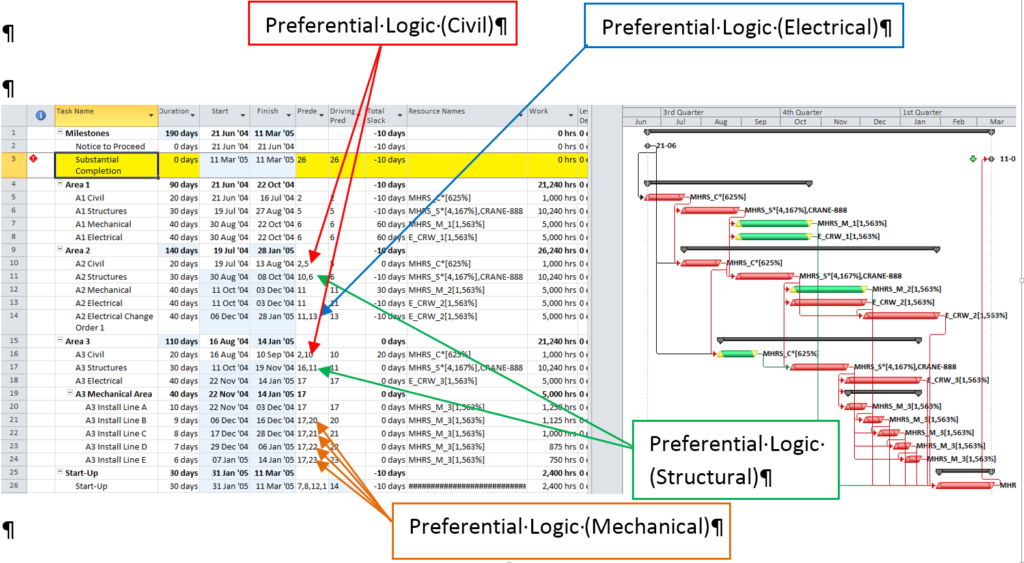
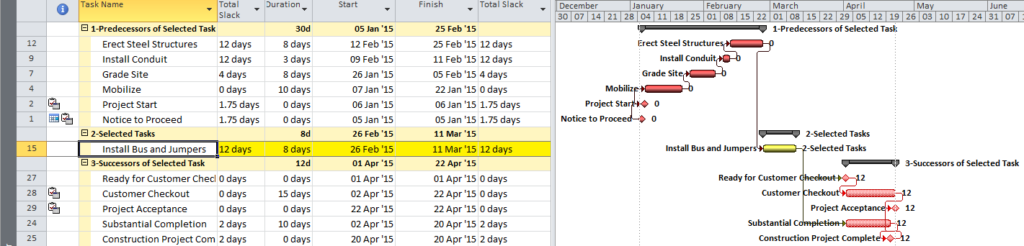
Often, when presented with a new project schedule in Microsoft Project, my first step (in concert with a logic health check) has been to run a Longest Path Filter analysis using BPC Logic Filter. This report quickly and clearly identifies the driving path to project completion. While the resulting filtered task list is useful for reporting, it rarely satisfies the needs of a serious analysis. The second step, therefore, is to identify the associated near-longest-paths of the project by running a “Task Logic Tracer” predecessor analysis – with a positive relative float limit – for the project completion task. The result is a clear description of the driving and near-driving paths to project completion. The latest release of BPC Logic Filter adds a specific command to combine these two actions and generate a single “Near Longest Path Filter” for the project.
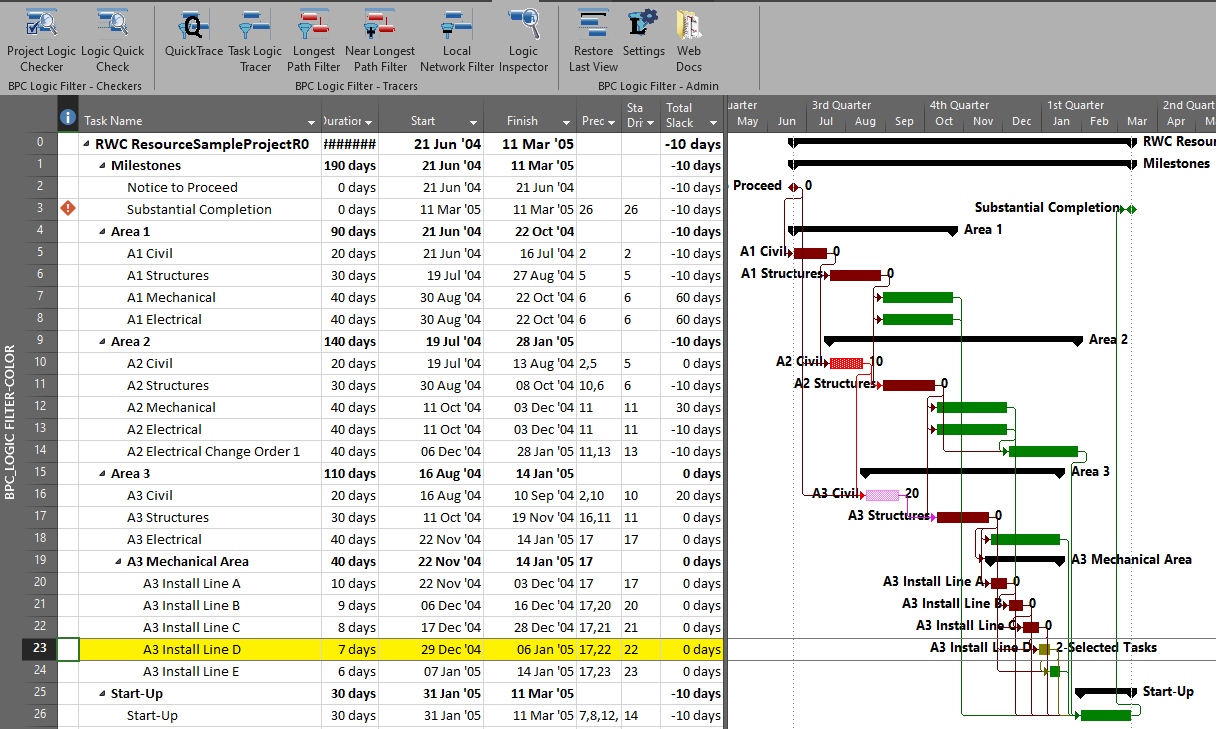
The mechanics are pretty simple. As usual – with a Gantt view active in a project that contains logic – just open the Add-Ins ribbon [changed to the BPC ribbon in subsequent versions] and click on the button for “Near Longest Path Filter.”
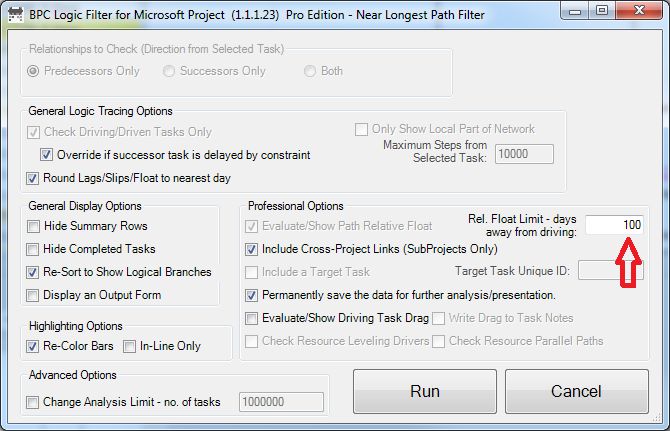
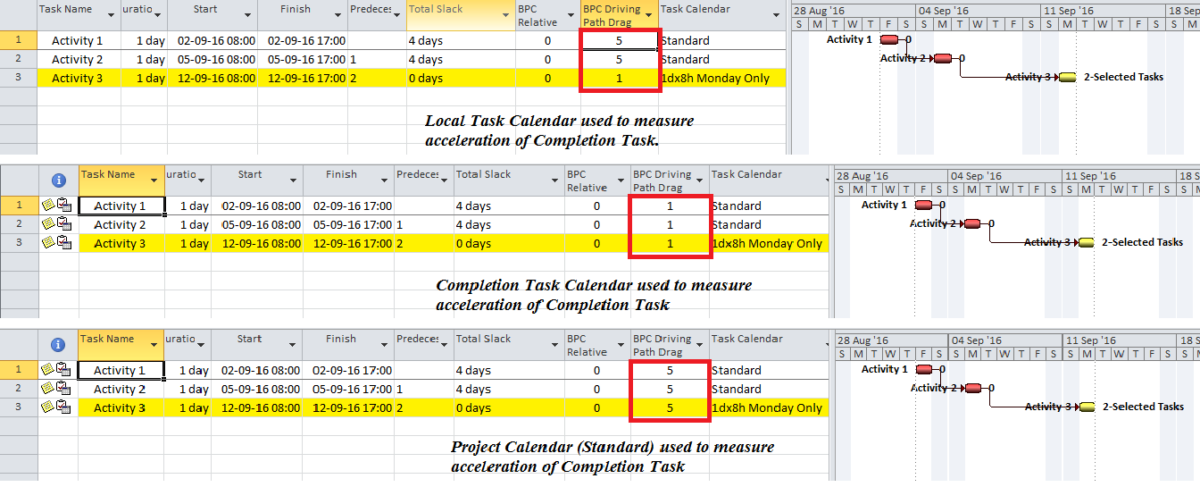
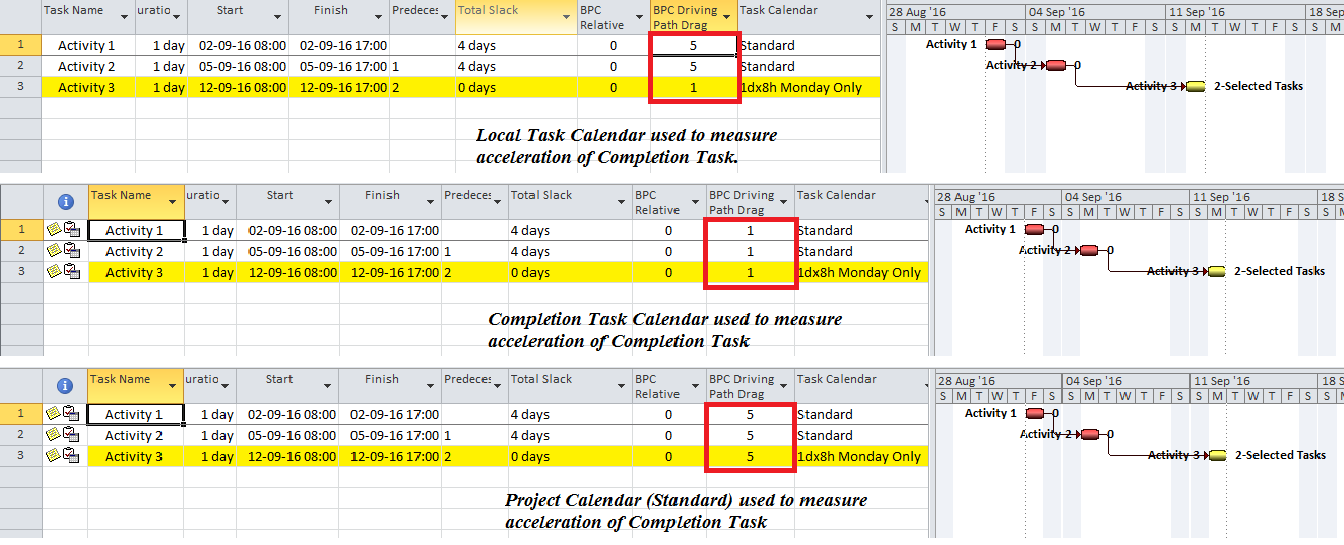
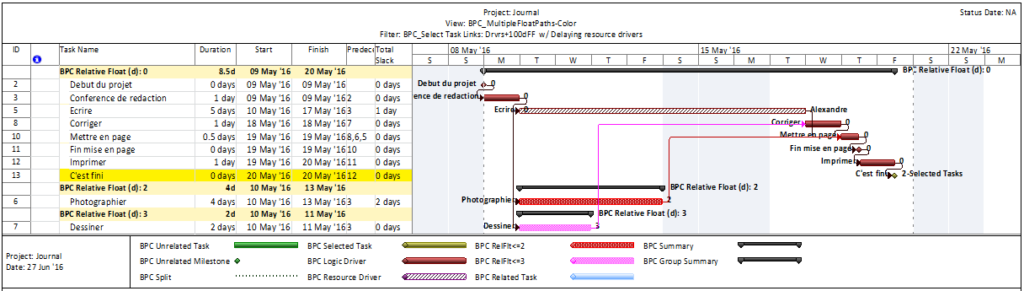
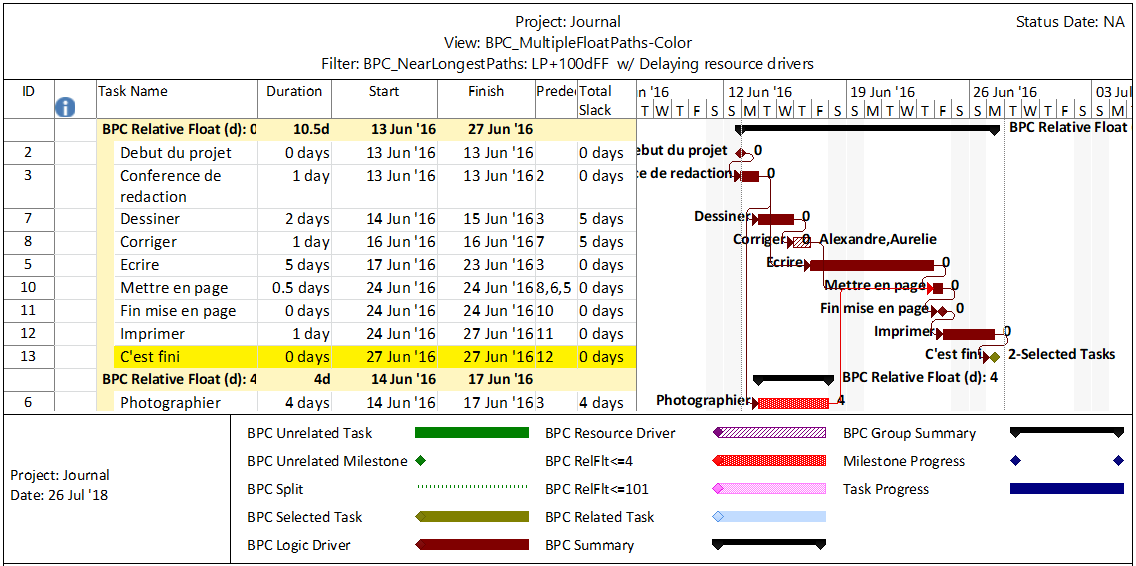
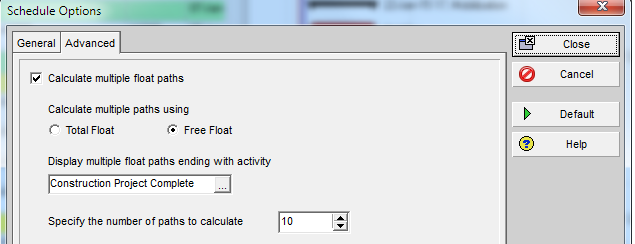
The add-in will initialize, and the user is given a choice of modifying the default analysis parameters. Some of the parameters are pre-set and can’t be changed here. The key parameter for a formal Near-Longest-Path analysis is the Relative Float Limit, highlighted below. Any related task with a Path Relative Float that is less than the specified limit will be included in the filter; all others will be ignored and considered unrelated. The default value is 100 days away from the driving/longest path (which can be changed in the Settings).
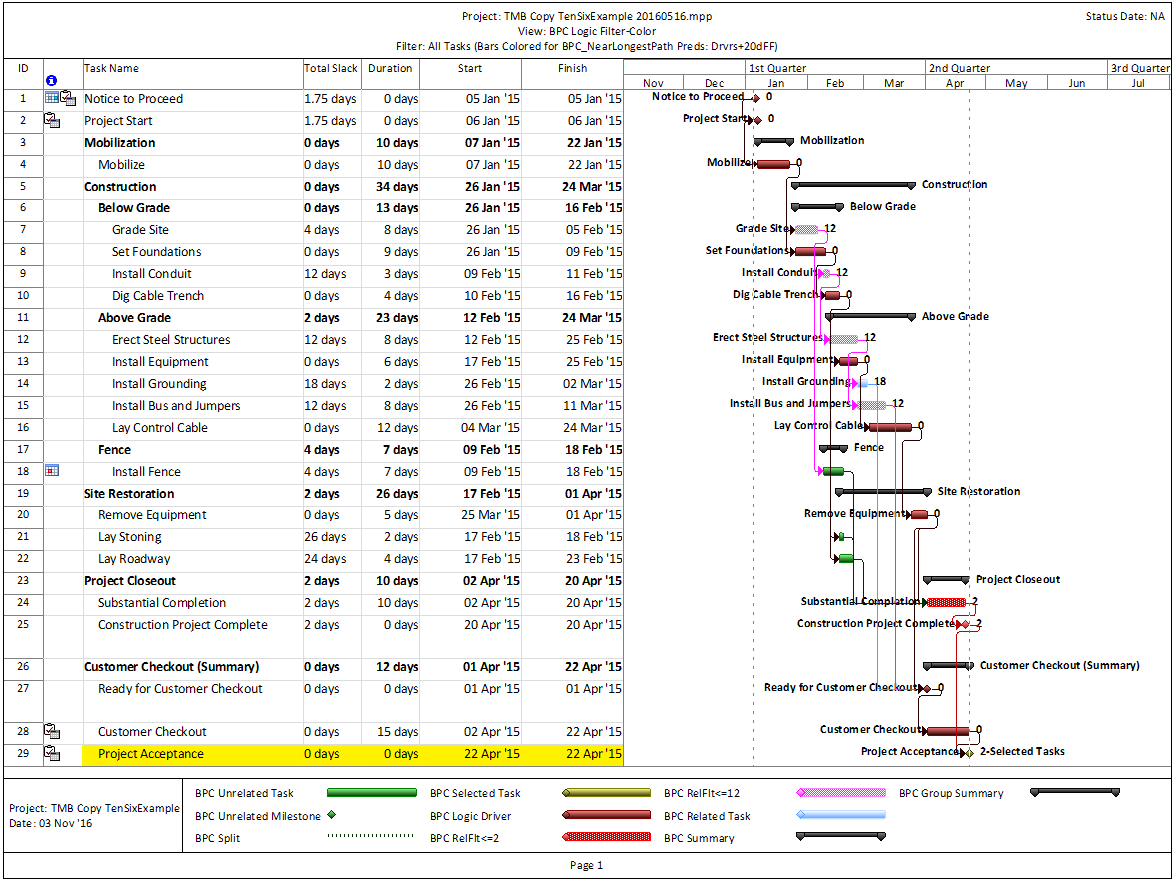
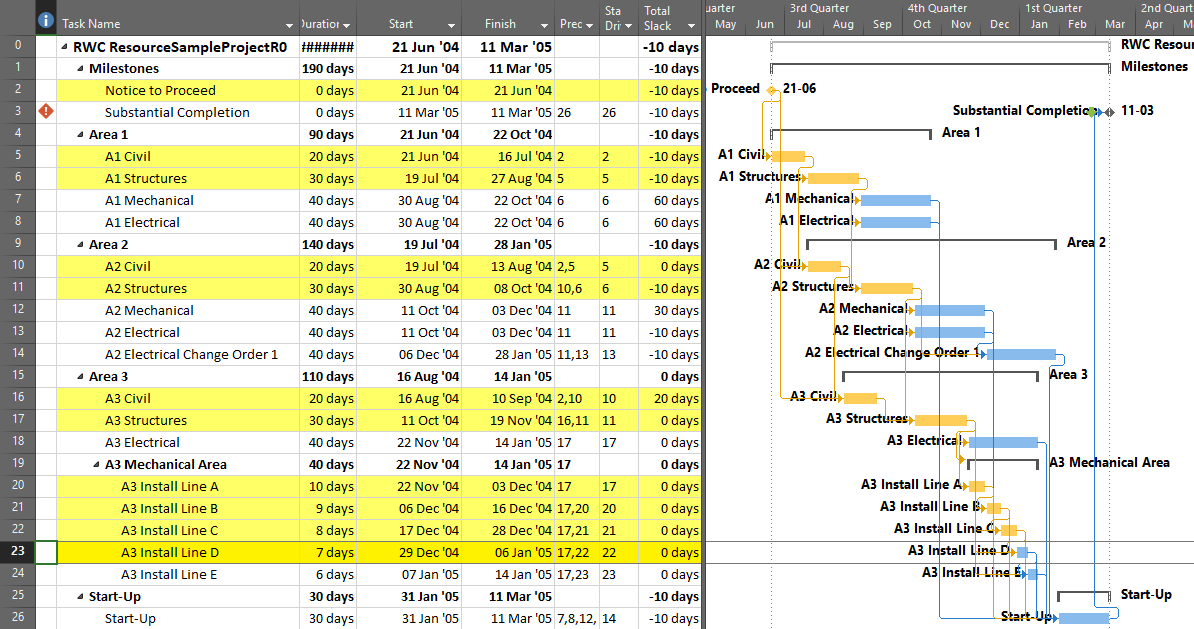
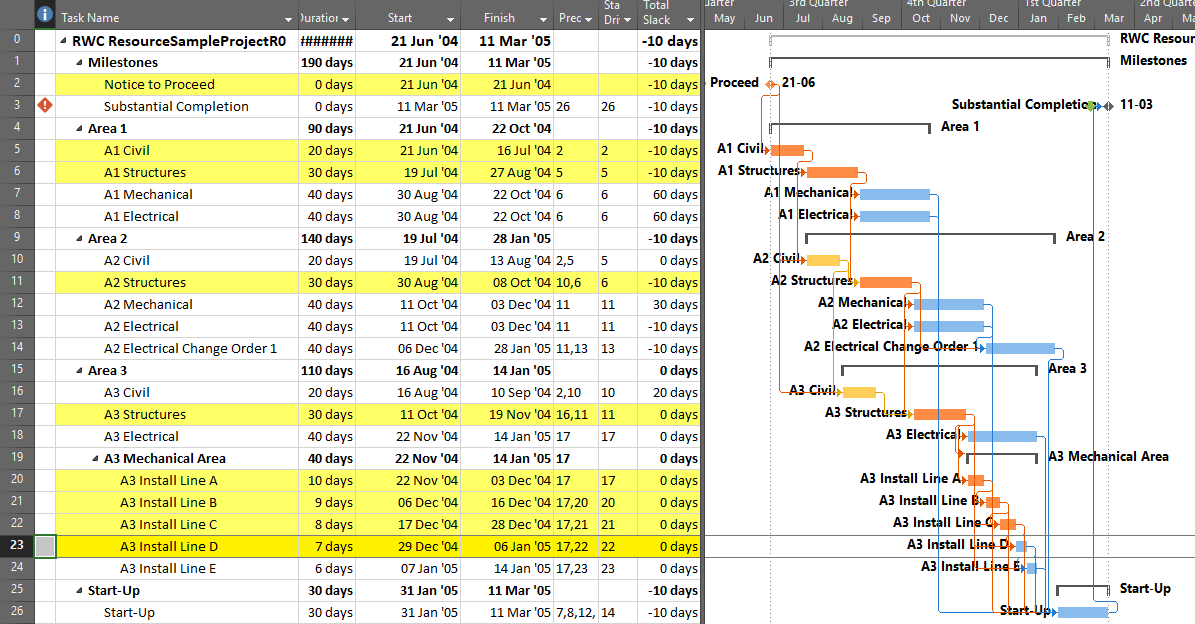
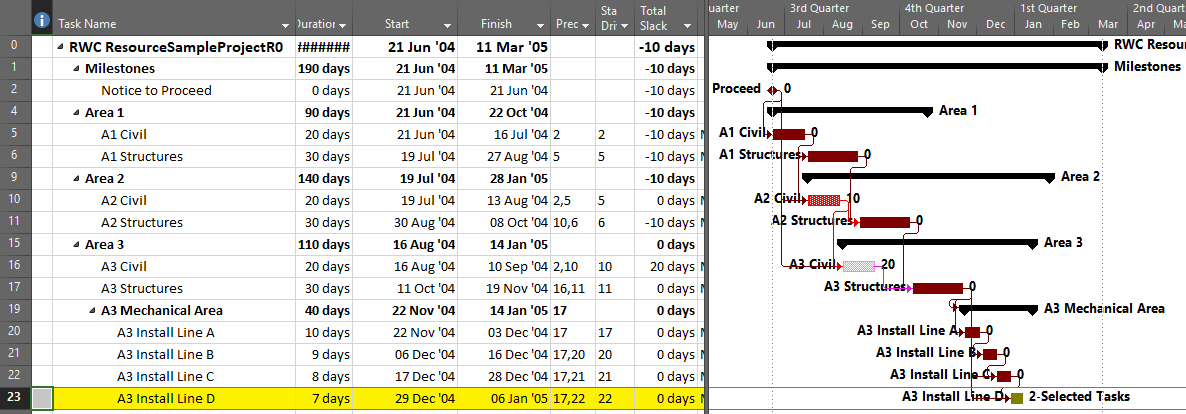
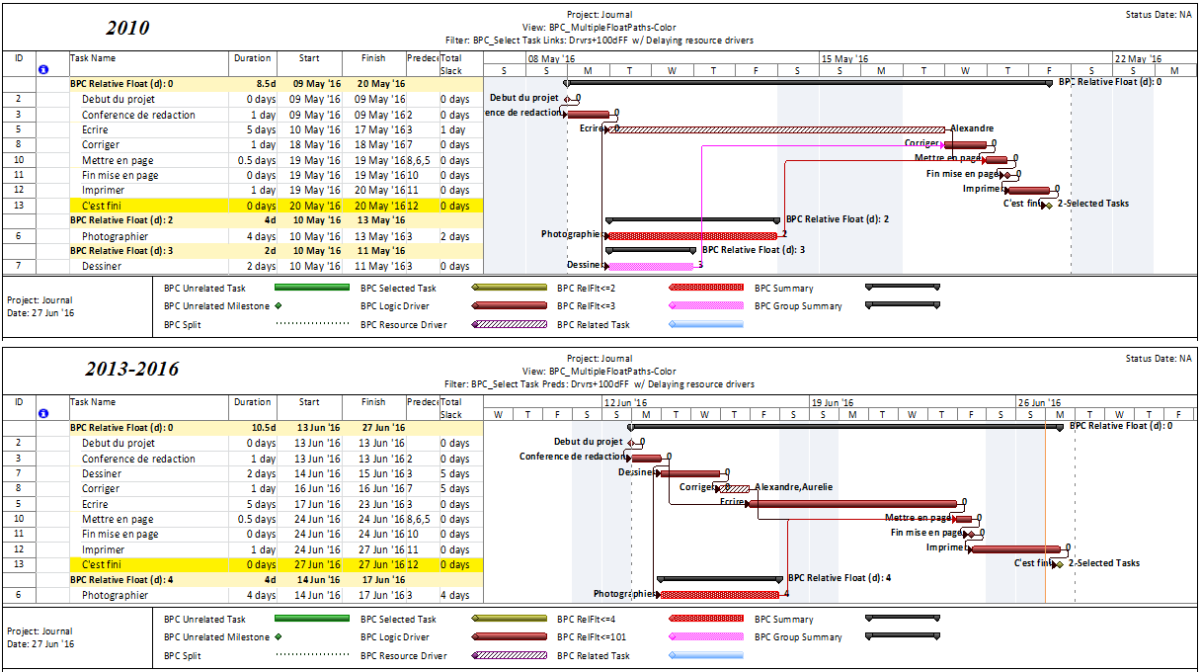
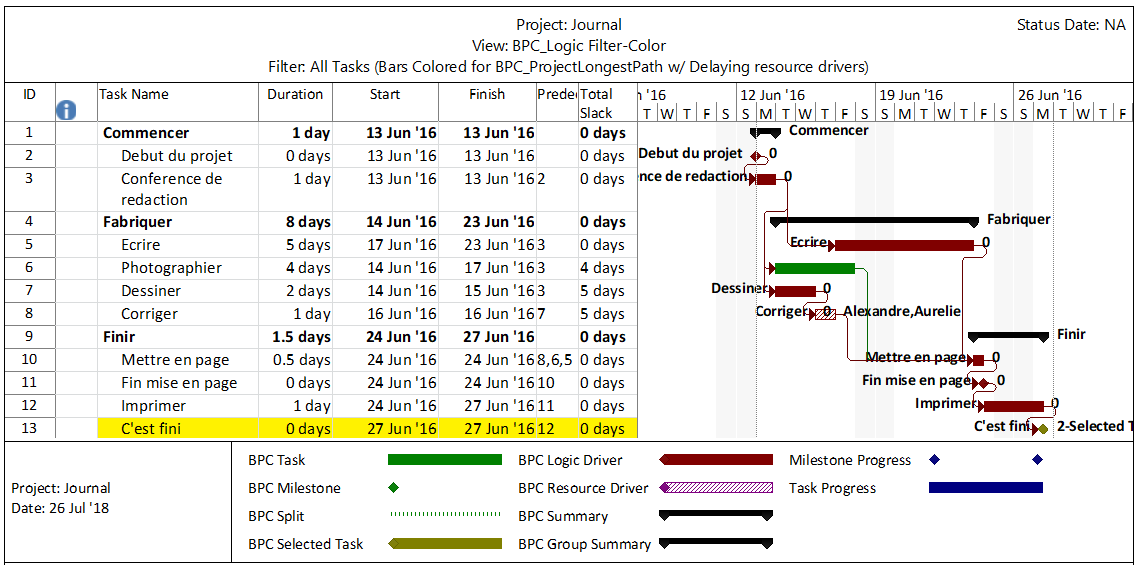
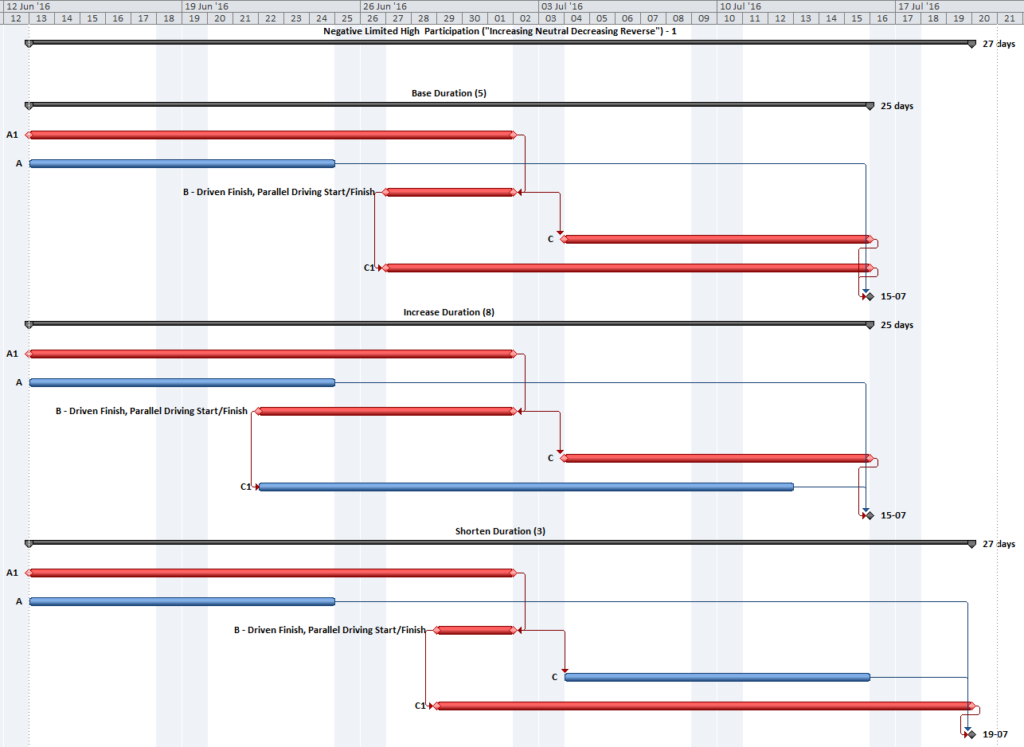
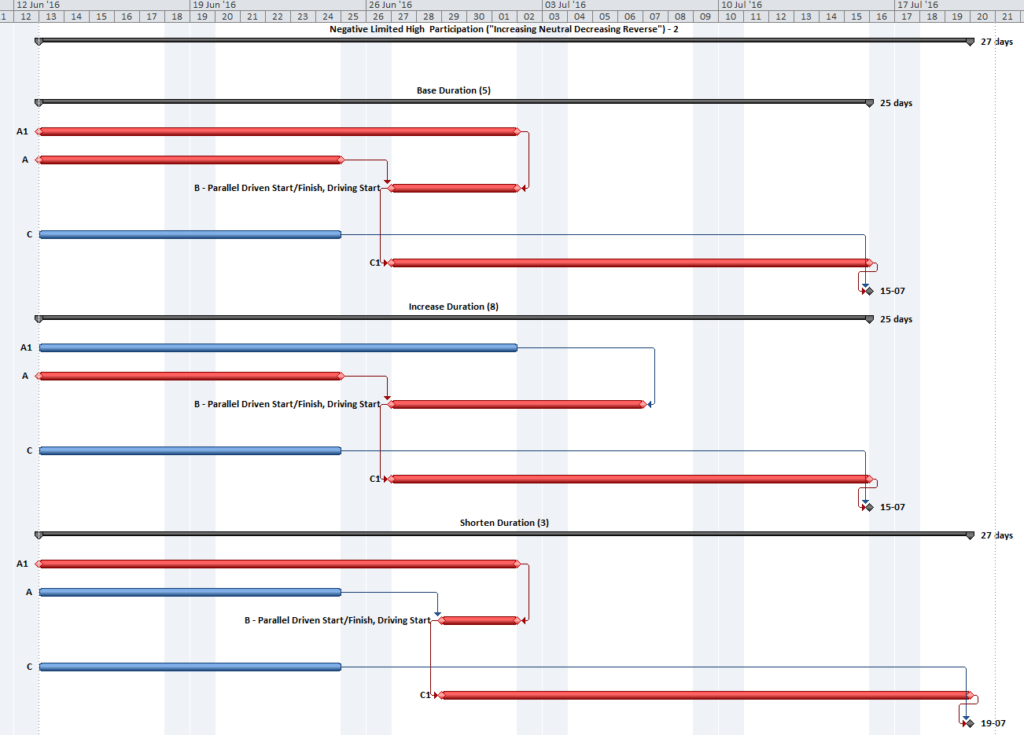
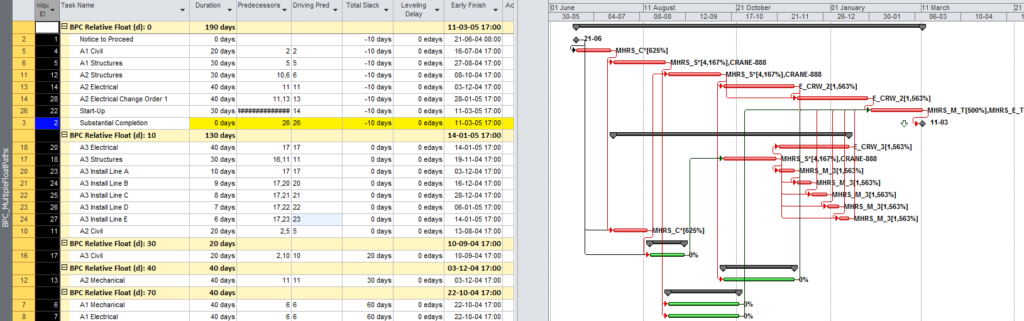
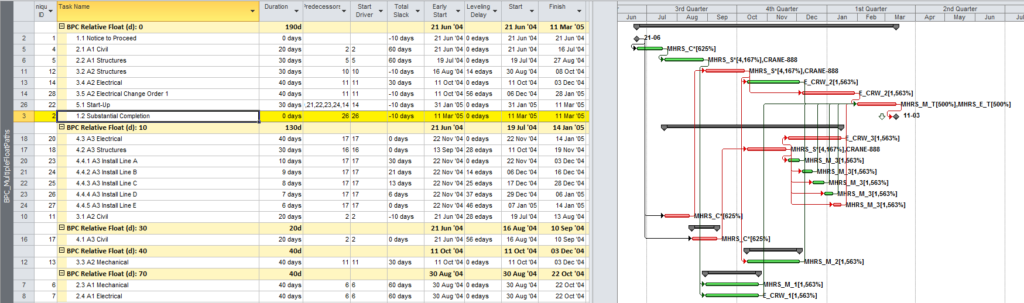
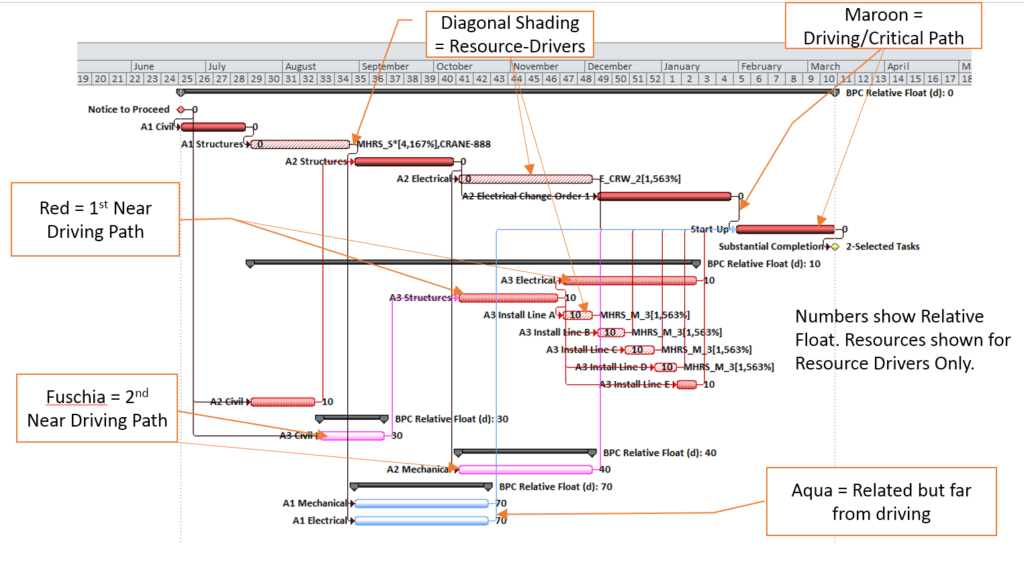
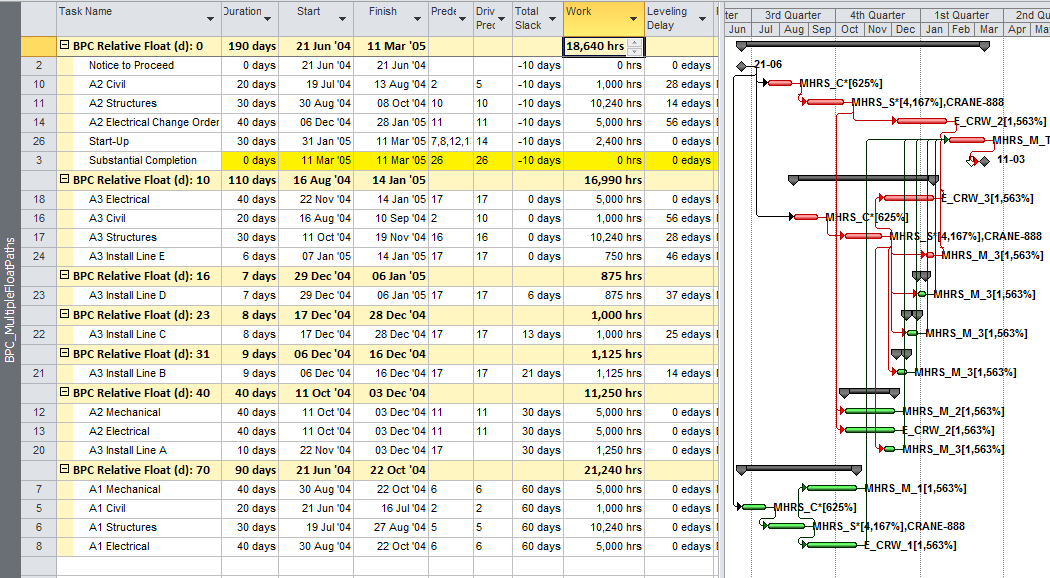
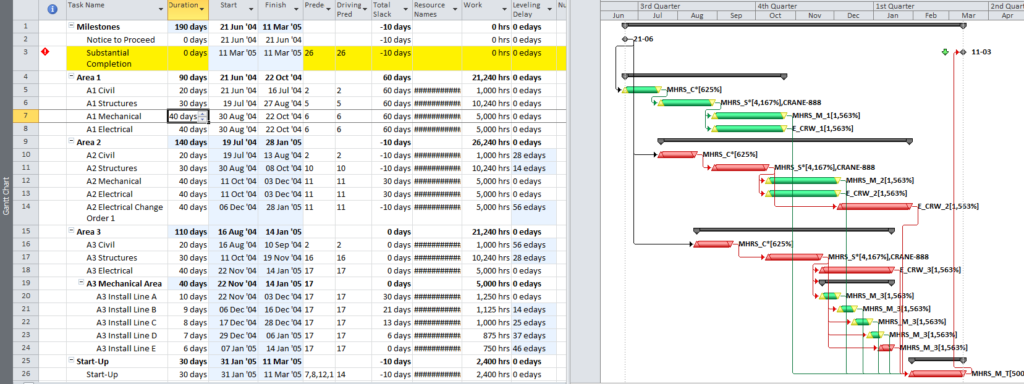
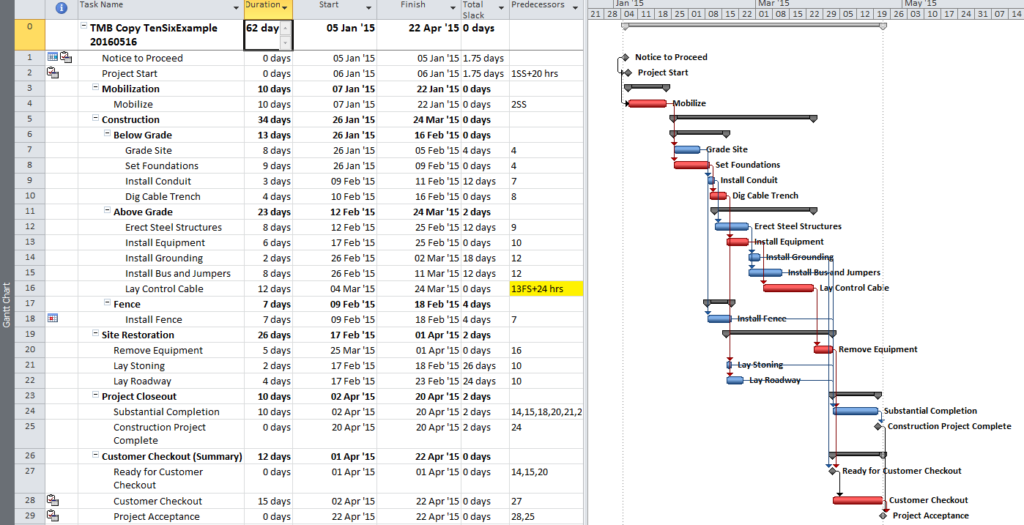
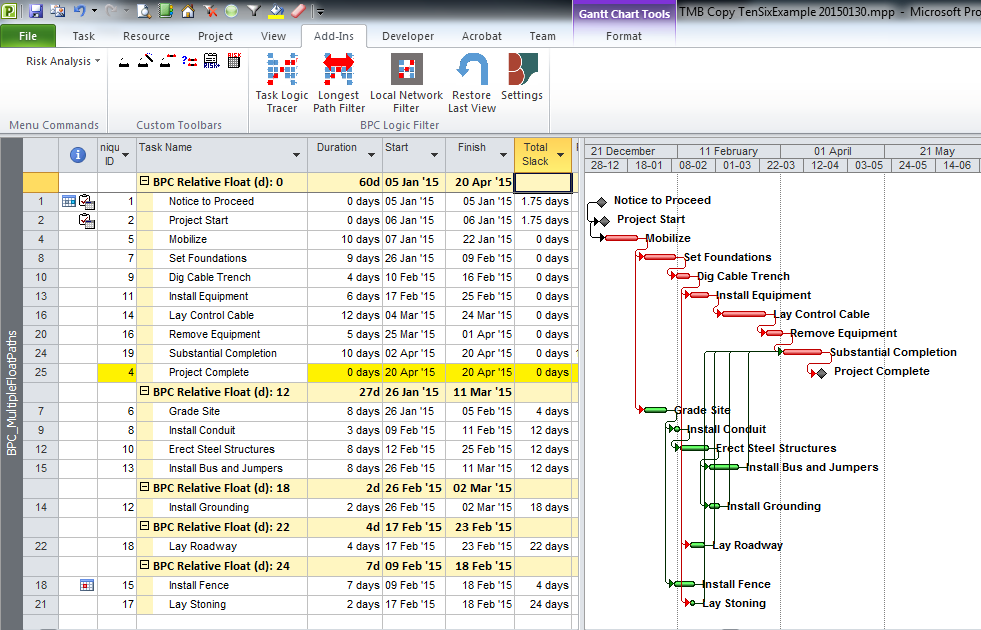
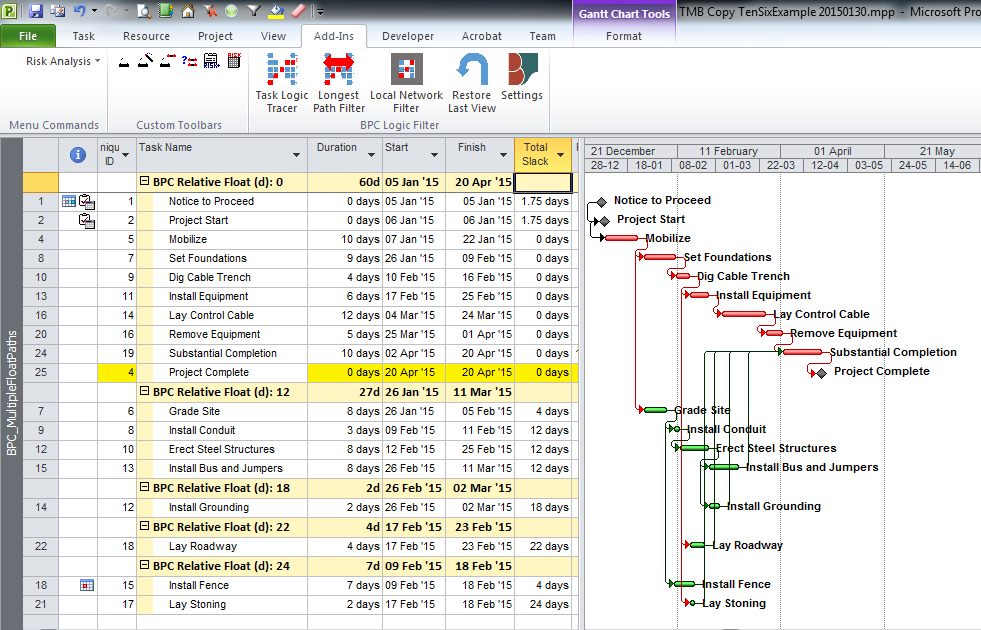
The standard output for a simple project (using the parameters selected above) is provided here. Selecting “Re-Color Bars” instructs the add-in to generate the custom output shown, including the header, the legend, and five different bar colors depending on proximity to the Longest Path. Thresholds for applying these bar colors can be manually adjusted in the program settings or, if desired, automatically adjusted by the add-in. 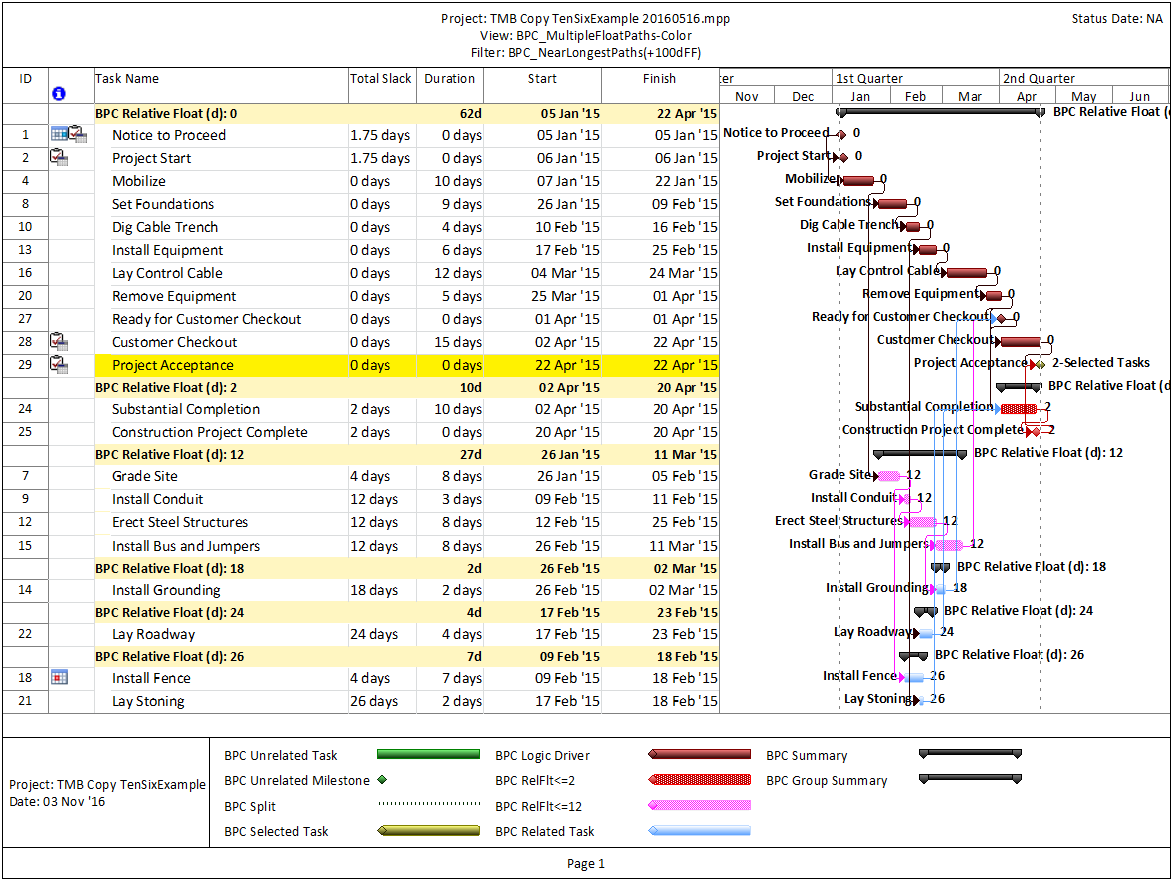
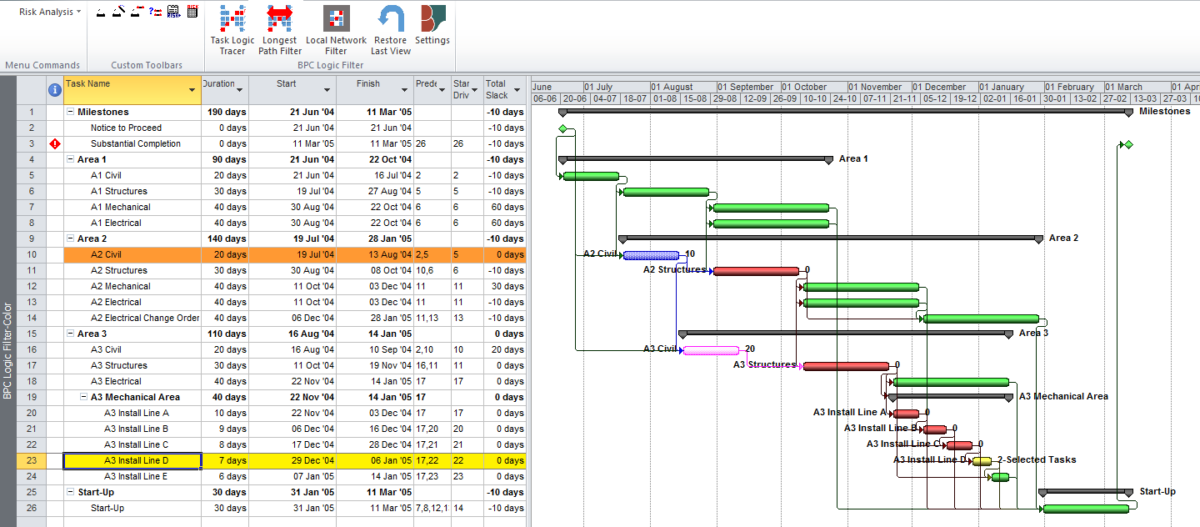
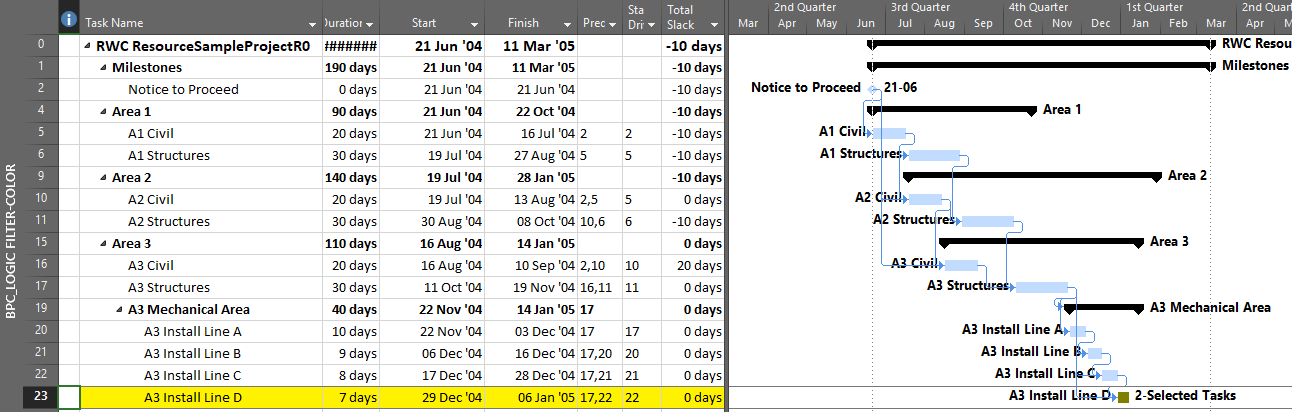
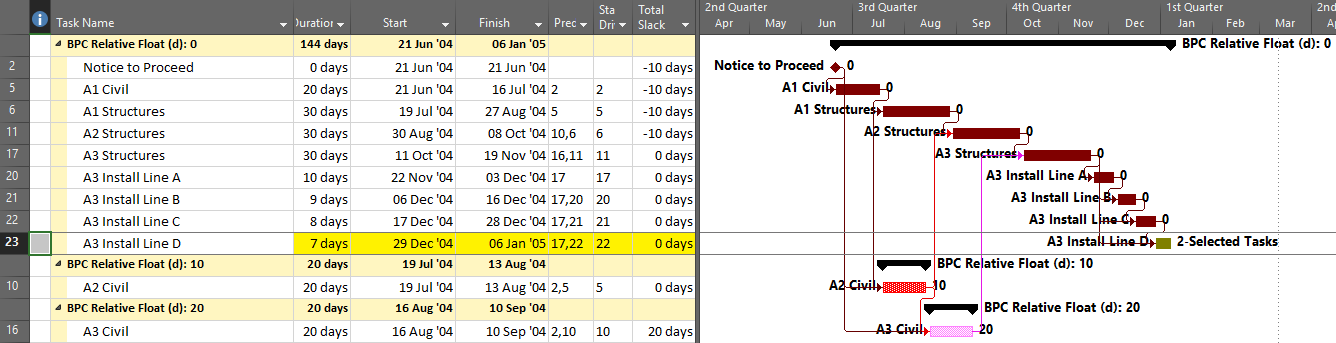
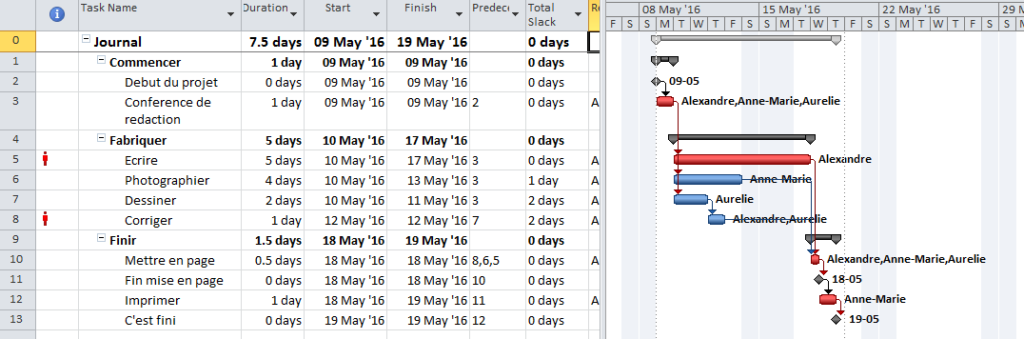
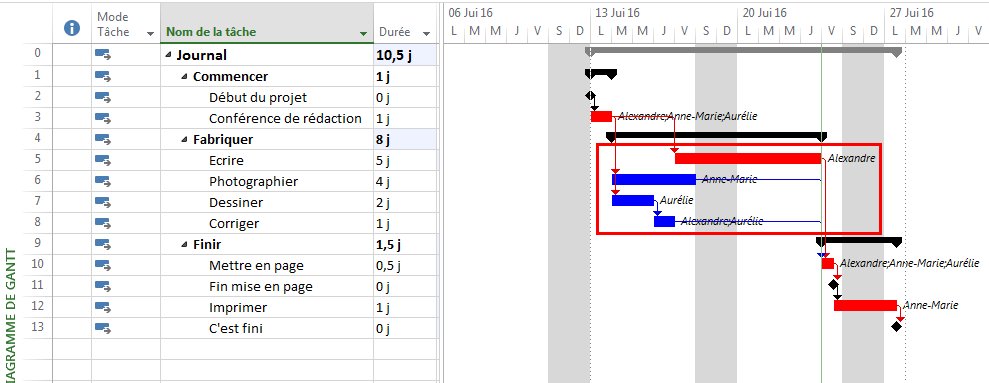
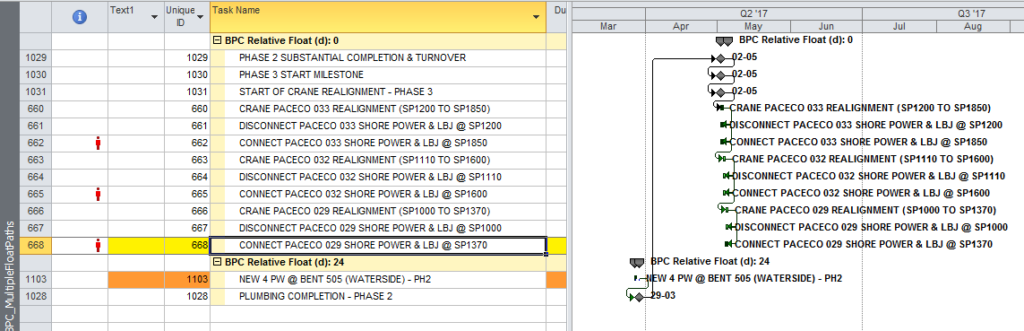
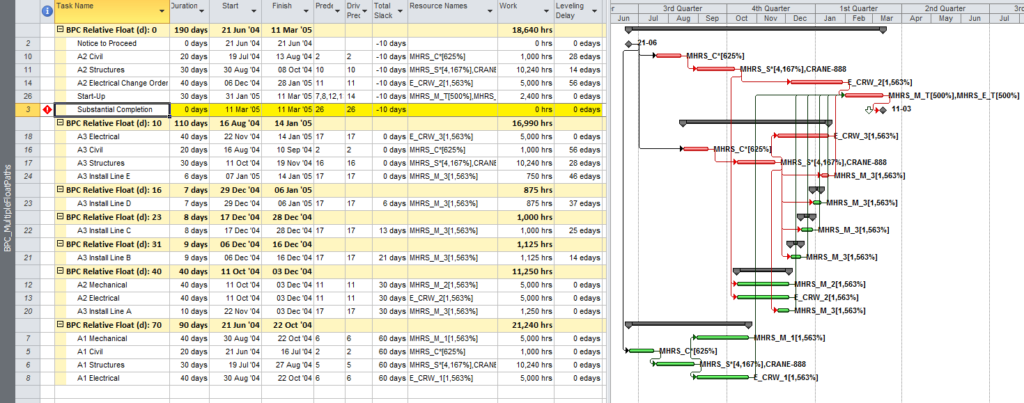
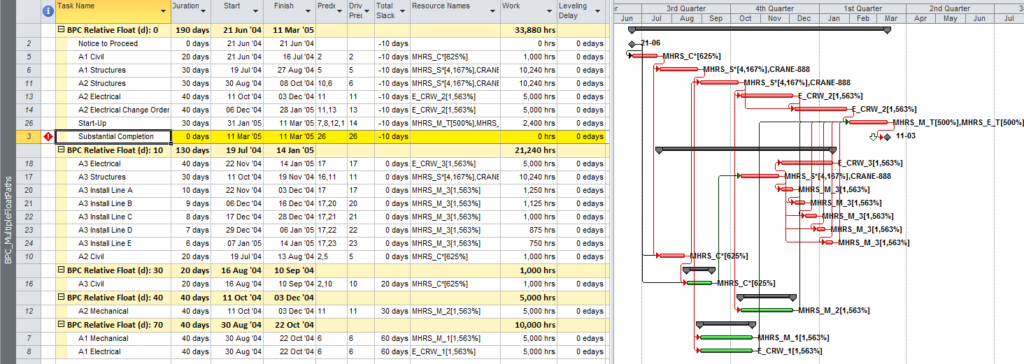
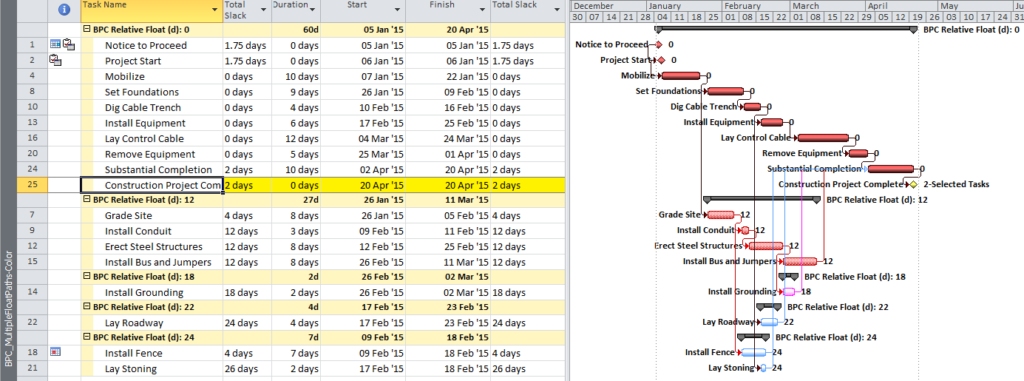
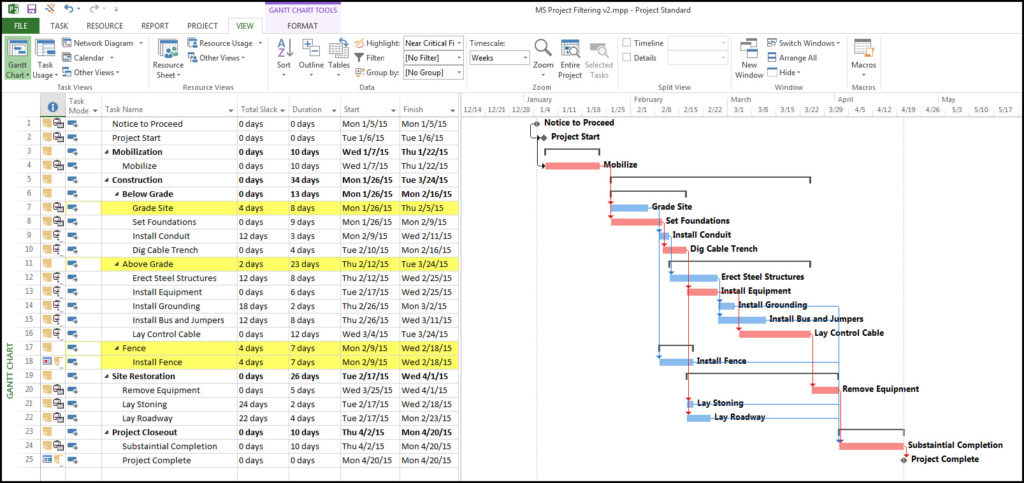
Here’s an alternate view showing the Near Longest Paths in-line in the context of an existing Outline/WBS organization. In this analysis I reduced the Relative Float Limit from 100 to 20 days, and the three tasks at the bottom of the earlier figure were ignored. Here they are given a green “BPC Unrelated Task” bar.
While I’ve always hated redundant work, this particular improvement to BPC Logic Filter was kick-started by my recent review of the draft of “Analyzing Near-Critical Paths,” a pending Recommended Practice from AACE International. The new draft recommended practice is based largely on the previously-published (2010) Recommended Practice 49R-06 – Identifying the Critical Path. According to both documents, Critical- and Near-Critical paths may be identified on the basis of total float/slack thresholds (in the absence of variable calendars, constraints, or other complicating factors) and – when total float/slack does not suffice – “closeness to the longest path.” For the latter cases, 49R-06 suggests two methods of analysis:
- Longest Path Value – a metric that appears similar to Path Relative Float (in BPC Logic Filter) for the project completion task. This metric has been applied as an add-on to Oracle Primavera scheduling tools: See Ron Winter’s Schedule Analyzer.
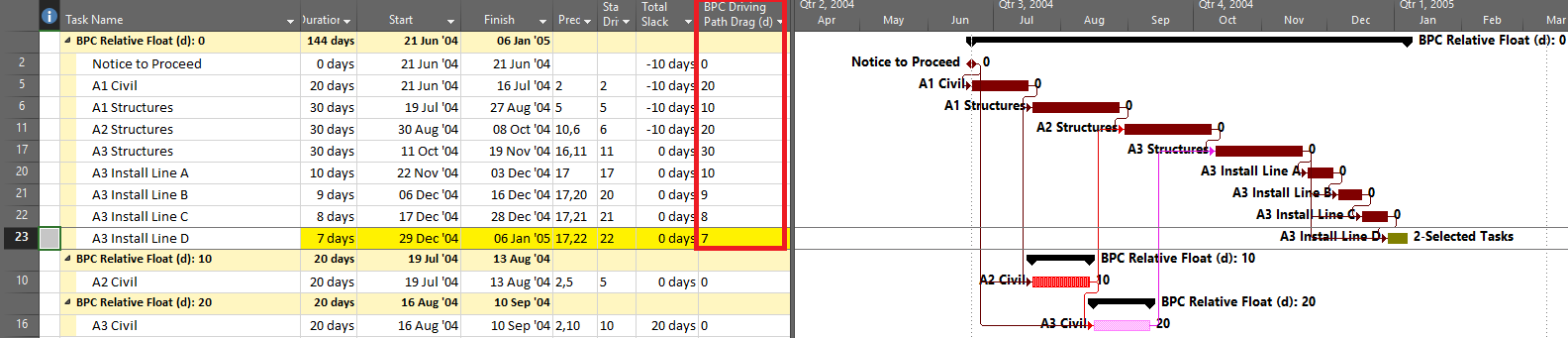
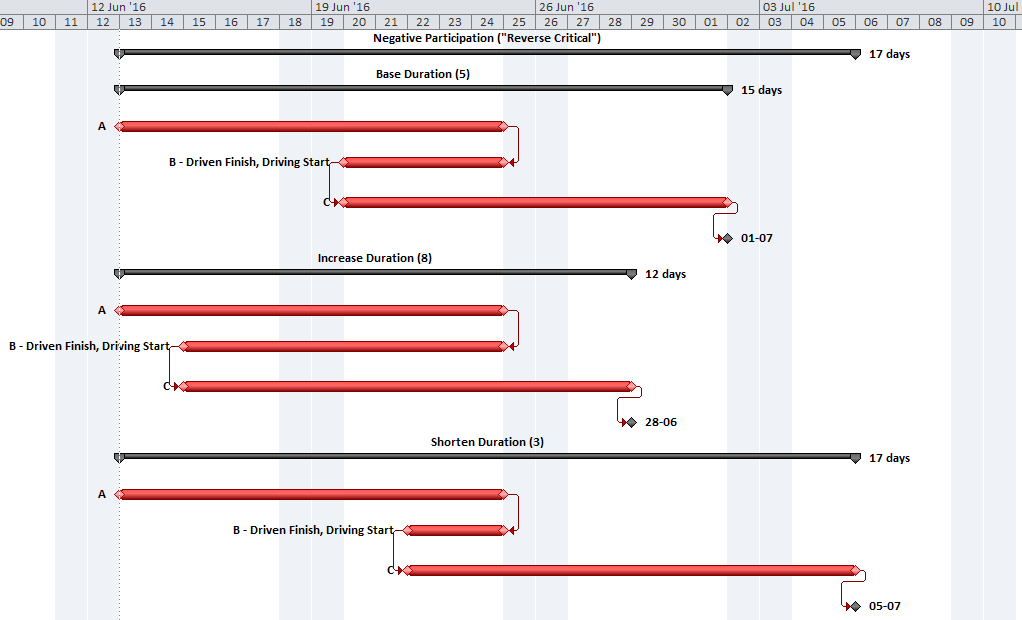
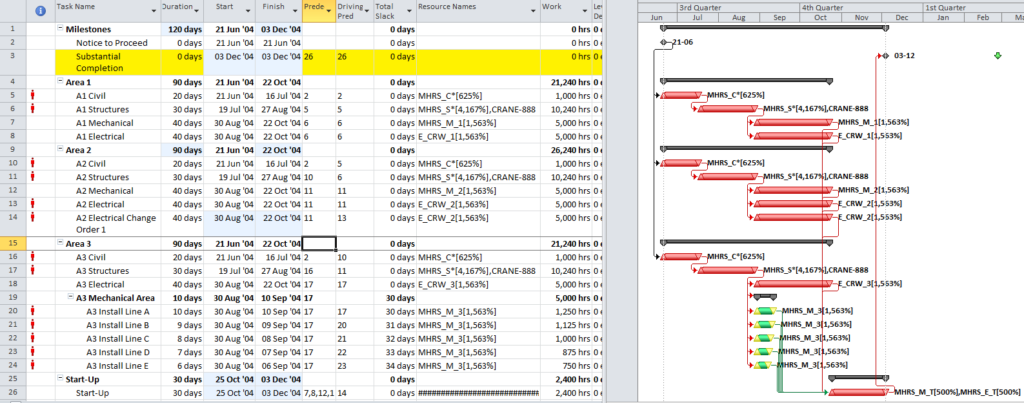
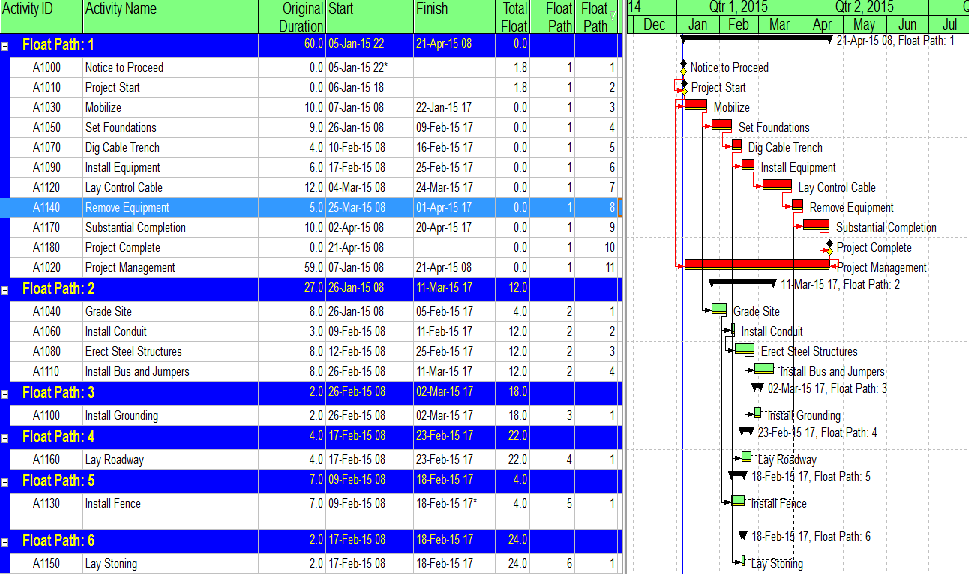
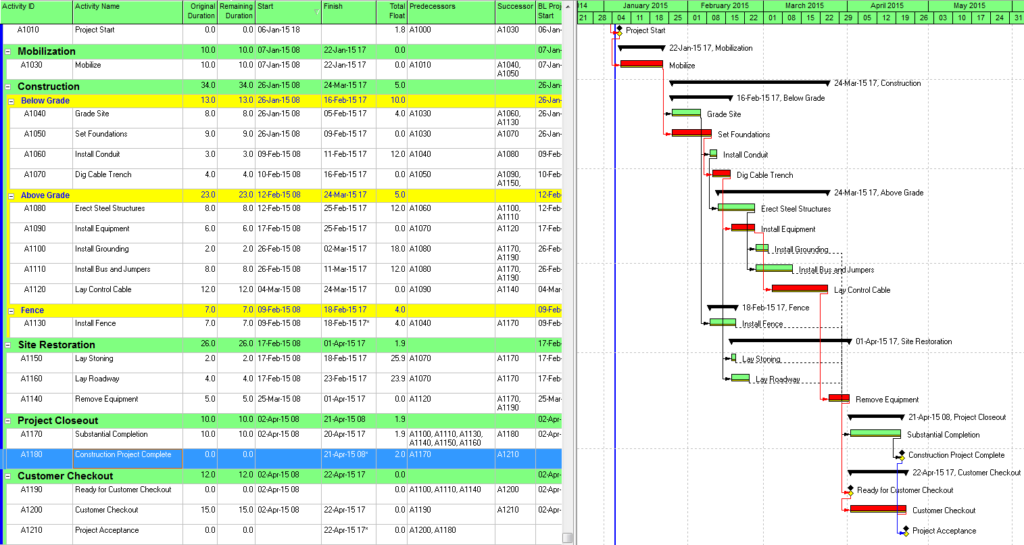
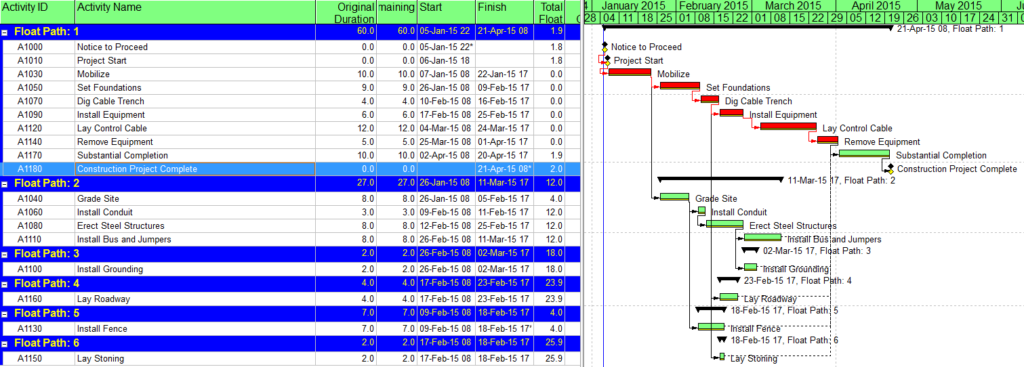
- Multiple Float Path analysis. Like the Longest Path Value, Multiple Float Path analysis is primarily associated with Oracle’s Primavera scheduling tools – it is presented as an advanced scheduling option in P6. As I’ve noted in Beyond the Critical Path – multiple float path analysis indicates closeness to the longest path without explicitly measuring and presenting it. Detailed examination of the results, including relationship free floats, is necessary to determine the apparent relative float of each activity.
From its start, BPC Logic Filter has supported a similar analysis for Microsoft Project schedules through its Path Relative Float metric, Multiple-Float-Paths views, and other reporting. The new “Near Longest Path Filter” offers a single-step approach to identifying and analyzing near-critical paths in the presence of variable calendars, constraints, and other complicating factors – when Total Slack becomes unreliable as an indicator of logical significance.
See also Video:
Video – Analyze the Near-Longest Paths in Microsoft Project using BPC Logic Filter