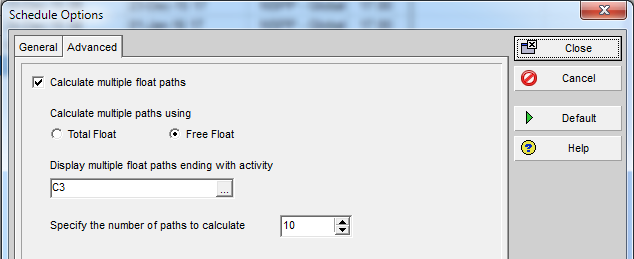
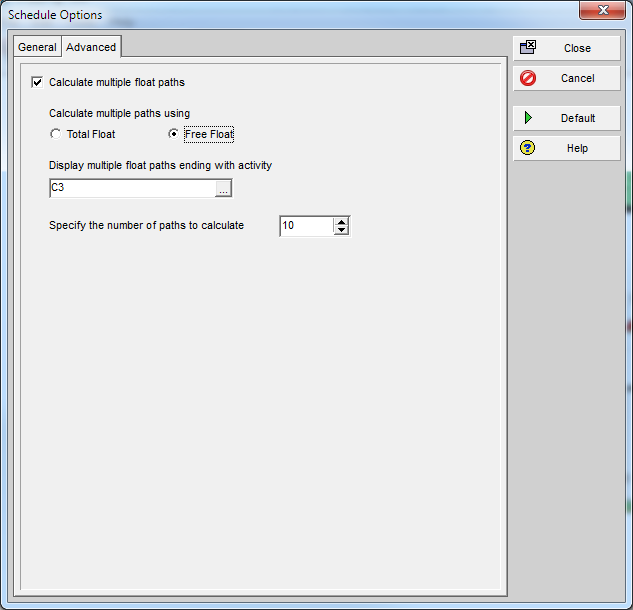
In Oracle Primavera P6, Multiple Float Path analysis is useful for identifying and organizing logic paths leading to a selected End activity in a schedule. If the Driving Logic to the End activity is desired, then the Free Float option should be selected.
When I wrote about P6’s Multiple Float Path (MFP) analysis here, I suggested using the Free Float option for identifying driving logic paths. Since then, I’ve encountered more than a few professionals who believe that the Total Float option also identifies driving logic. This entry provides a simple example illustrating why that is not always the case. [For a much more detailed review, have a look at our technical paper on interpreting logic float paths in P6.]
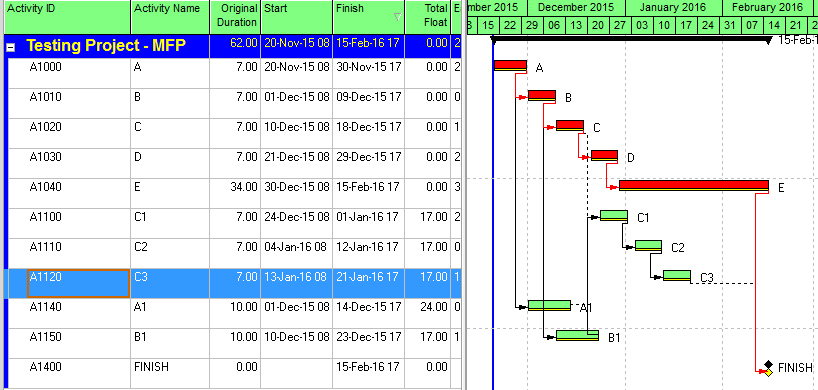
This “Testing Project – MFP” is a simple project that includes no constraints and only a single calendar (5dx8h). Both “Longest Path” and “Total Float” criteria lead to the same Critical Path: A-B-C-D-E-FINISH. There are several non-critical branches from the Critical Path: namely A1, B1, and C1 are successors to A, B, and C respectively. C1 is the start of the non-critical branch: C1-C2-C3. It has both A1 and B1 as predecessors, and it is driven by B1.
For this project, it is obvious (and a trivial exercise to demonstrate) that the driving logic path for any Critical Path activity is comprised of its “Critical” predecessors; i.e. those activities that are predecessors of the selected End activity and which have zero Total Float (TF=0).
What if we are primarily interested in the driving logic to an End activity that is NOT on the Critical Path – activity C3 for example? By simple inspection of the schedule (or by click-tracing from C3 backward through “driving” relationships), it is easy to see that C3’s driving logic path is comprised of the following activities: A-B-B1-C1-C2-C3. Since Total Float varies along this path (0-0-17-17-17-17), it is clear that driving logic for C3 is not associated with Total Float.
Another way to examine the logic controlling activity C3 is to re-schedule the project while calculating multiple float paths. MFP analysis examines the predecessor activities leading to a selected End activity (C3 in this case) in order of their logic sequence and assigns each of these (excluding LOE activities) to a numbered Float Path. Float Path 1 is “the most critical path.” The analysis stops when the specified number of float paths is reached. Afterward, organizing the schedule by Float Path and sorting by Float Path Order leads to a clear differentiation of logic sequence paths. I also routinely filter-out activities without float path assignment and activities with ALAP constraints. The construction of the various float paths is governed by which float option is selected – either Total Float or Free Float – in the advanced schedule options.
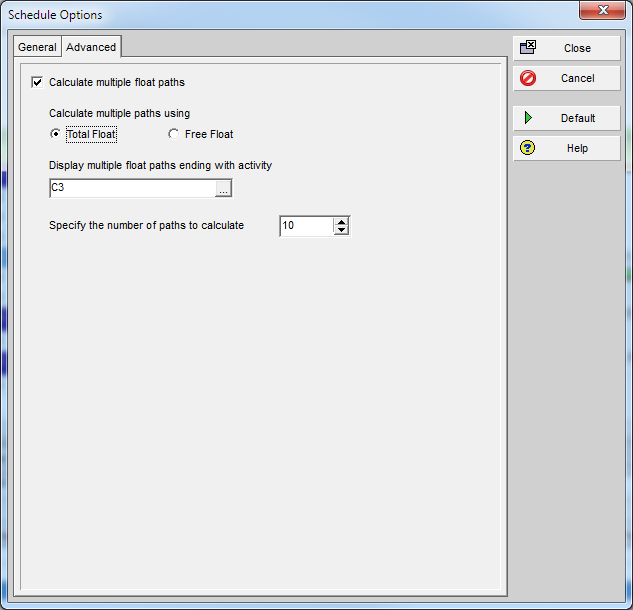
Total Float Option
This is what the P6 Help file says for the Total Float option.
Total Float – Choose this option to identify critical paths based on the total float of activity relationships. To calculate the most critical path, the module first determines which relationship has the most critical total float. Using this relationship as the starting point, the module determines which predecessor and successor activities have the most critical relationship total float, among all possible paths, until an activity is reached that does not have any relationships. The path that contains these activities is the most critical path.
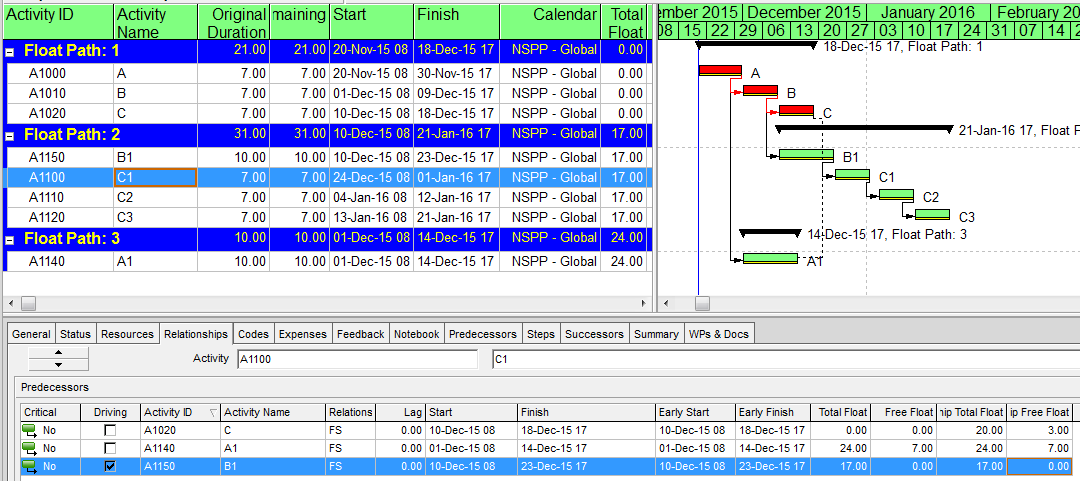
Using the Total Float option and the other parameters shown for our simple project leads to the result shown below. Float Path 1 is limited to those activities that 1) are predecessors of C3, AND 2) have a Total Float of 0. According to P6, this is “the most critical path.” Float Path 2 is comprised of C3’s predecessors (and C3 itself) that have a Total Float of 17. Float Path 3 comprises the single logical predecessor of C3 with TF = 24. Thus, float paths appear to correspond to Total Float alone.
[Sep’19 Edit] I’ve recently read the only public foundation document for the Total Float algorithm – originally called “Enhanced” PDM in 2004 – and the observed behavior is as expected according to that algorithm. Essentially, Float Path 1 is “seeded” by whichever path-predecessor of C3 has the lowest total float (subject to some tie breakers.) Once seeded, the path is defined/traced by “bi-directional driving” relationships from the seed point. A “bi-directional driving” relationship exists when:
- The Relationship Total Float equals the total float of the predecessor activity; AND
- Relationship Successor Free Float = 0. (P6 support docs point to the “most critical” Relationship Successor Total Float here, but that didn’t stand up to close scrutiny.)
Subsequent float paths are seeded and traced using the same priorities.
Fundamentally, the algorithm was developed to a) differentiate float-based critical paths and near-critical paths in the presence of multiple calendars; and b) differentiate independent driving logic paths, including multiple critical paths, that share the same total float. So here in the absence of calendars or parallel critical paths, the alignment of the calculated float paths and total float is exactly as expected.
Clearly, none of the 3 float paths from the Total Float option correspond to the actual Driving Path to activity C3. Path 1 includes activity C, which although it is on the Project’s Critical Path is NOT on the Driving Path to activity C3. The actual Driving Path has been split between Float Path 1 and Float Path 2.
Thus, using Total Float option, Float Path 1 – “the most critical path” – comprises those activities that are predecessors of activity C3 and have the lowest total float. C3’s own driving/controlling logic path is not defined by the float paths assigned.
Free Float Option
This is what the P6 Help file says for the Free Float option.
Free Float – Choose this option to define critical float paths based on longest path. The most critical path will be identical to the critical path that is derived when you choose to define critical activities as Longest Path in the General tab. In a multicalendar project, the longest path is calculated by identifying the activities that have an early finish equal to the latest calculated early finish for the project and tracing all driving relationships for those activities back to the project start date. After the most critical path is identified, the module will calculate the remaining sub-critical paths.
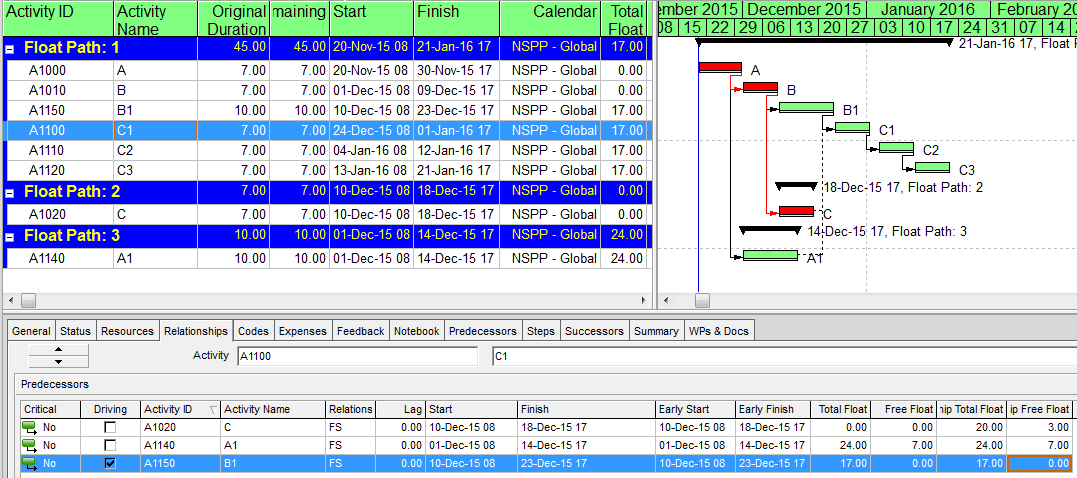
Using the Free Float option and the other parameters shown for our simple project leads to the result shown below. Float Path 1 exactly corresponds to the known Driving Path to activity C3: i.e. A-B-B1-C1-C2-C3. Float Path 2 is comprised of activity C only, while Float Path 3 is comprised of activity A1 only. Float paths clearly have no correspondence to Total Float.
The key decision point in allocating float paths seems to occur at the predecessors to activity C1: i.e. C, A1, and B1.
- C has an activity Total Float of 0. The C-C1 relationship has a Relationship Total Float of 20 and a Relationship Free Float of 3.
- A1 has an activity Total Float of 24. The A1-C1 relationship has a Relationship Total Float of 24 and a Relationship Free Float of 7.
- B1 has an activity Total Float of 17. The B1-C1 relationship has a Relationship Total Float of 17 and a Relationship Free Float of 0.
Although the Help file is essentially silent on the issue, the MFP analysis appears to allocate these predecessor activities to the three float paths on a basis that correlates to Relationship Free Float. Here, a Relationship Free Float of zero indicates a Driving Relationship. Successively higher values of relationship free float correspond to less-driving relationships and result in assignment to higher-numbered float paths.
Thus, using Free Float option, Float Path 1 – “the most critical path” – comprises the driving path to the selected end activity. Higher-numbered float paths correspond to “sub-critical” paths, or to successively less-driving paths to the selected end activity.
[Jul’18 Amendment – Unfortunately, the ordering of these “sub-critical” paths can be counter-intuitive, with true “Longest Path” activities sometimes being relegated to high-numbered float paths. See Relationship Free Float and Float Paths in Multi-Calendar Projects (P6 MFP Free Float Option).]
Significance of Total Float
The “Critical Path” of a logic driven project schedule is the collection of activities that determine the earliest possible completion date of the project – i.e. the driving logic path to project completion. In the original Critical Path Method and its variants, the Critical Path was reliably correlated to a Total Float value of zero, and delay (or acceleration) of any Critical Path activity cascaded directly to the project completion milestone. Near-critical paths were defined by successively higher values of Total Float. In simple projects, therefore, Total Float is a reliable indicator of the logical association between any given activity and the project’s Completion.
Because of Total Float’s significance in the traditional definition of Critical and Near-Critical Paths, it is easy – but generally incorrect – to presume a logical association between two activities on the basis of their Total Float values. In the absence of any late constraints, multiple calendars, or resource leveling, then such associations may exist between certain critical or lower-float successors and their higher-float predecessors. Thus, running MFP analysis using the Total Float option may be expected to reveal driving and near-driving logic when the selected End activity is on the float-defined Critical Path. As shown in the example above, however, such an analysis does not reveal driving and near-driving logic when the selected End activity is not Critical.
When a project schedule includes multiple calendars, resource leveling, or a late constraint on any activity except the final one, then Total Float becomes unreliable for indicating the driving path to project completion. Similarly, it becomes less useful for identifying driving and near-driving logic paths to selected activities even when they are on the “Critical Path”. In projects with multiple calendars and modest progress updates, the float paths defined using the Total Float option can deviate substantially from both the known driving paths and simple Total Float-based paths. Under these conditions, the Free Float option is almost certain to provide a clearer view of the schedule logic driving an activity, regardless of its criticality.