This is a short article about the calculation and use of Relationship Free Float in Oracle Primavera P6, a project scheduling tool. [It amends my previous entry on Total Float and Free Float Options in P6’s Multiple Float Path Analysis. Both articles are further expanded (and corrected) by the technical paper presented at the 2020 Annual Meeting of AACE International. An alternate version of the paper is hosted on our website.]
[The following few paragraphs are cribbed (with some edits to reflect improved understanding) from my own contribution to a discussion on Planning Planet a few years ago.]
Traditional notions of Total Float and Free Float are tied to the activities in the network, but they are not sufficient for evaluating logical float paths in complex CPM schedules, especially when variable calendars and/or late constraints are imposed. Relationship floats are needed for identifying near-driving relationships and for multiple-float-path analyses.
Documentation seems very sketchy, but based on my own observations I believe relationship floats in P6 are calculated similarly to activity floats – that is
- The early and late dates of relationships are computed by treating them as activities (with single FS+0 links at each end) in the forward and backward passes through the network (Duration equals lag, normally zero).
- Relationship total float (RelTF) = relationship late finish (RelLF) – relationship early finish (RelEF);
- Relationship free float (RelFF) = (Early Date of Relationship Successor Activity, ES for “FS” and “SS” links, EF for “FF” and “SF” links) – RelEF
The calendars used for the calculations seem to be as follows:
- Early dates use predecessor calendar (from the forward pass)
- Late dates use successor calendar (from the backward pass)
- Relationship free float and total float use the predecessor calendar.
[Apr’19 Edit: Relationship Successor Total Float and Relationship Successor Free Float are derived from the same relationship dates, but using the successor calendar rather than the predecessor calendar. (Figures now show both measures of relationship free float.)]
With multiple calendars, the driving and near driving paths revealed by Multiple Float Path (MFP) analysis are only partly correlated to the Relationship Free Float (and Relationship Successor Free Float) values displayed by P6. These may require careful scrutiny to avoid misinterpretation in complex, multi-calendar projects, for the following reasons:
a) A relationship is “driving” when the successor activity possesses zero working time between the lag-adjusted predecessor and successor dates. That is, the Relationship Free Float – according to the SUCCESSOR’s calendar (“Relationship Successor Free Float”) – is zero.
b) The Relationship Free Float that P6 displays (and that P6 appears to use as the primary path-allocation parameter for Float Paths >1, using the “Free Float” option) is computed according to the PREDECESSOR’s calendar.
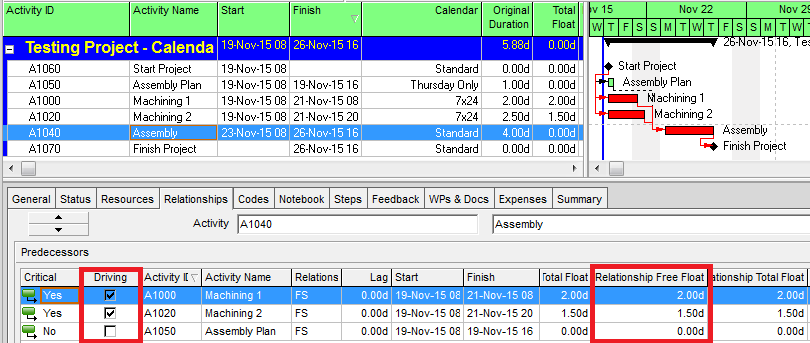
Consider the simple schedule illustrated below, wherein the “Assembly” activity has three predecessors whose calendars differ from Assembly’s. Assembly utilizes a standard 5-day calendar, while Machining 1 and Machining 2 are performed using automated equipment on a 7×24 calendar. The Assembly Plan must be prepared during a weekly resource coordination meeting that only happens on Thursdays.
As the figure shows, the Longest Path (red bars) is comprised of the two Machining activities (finishing 12 hours apart) followed by Assembly. As expected, both machining activities are marked as driving predecessors (there is zero relationship free float for either one according to Assembly’s calendar), and the Assembly Plan predecessor relationship is marked as non-driving.
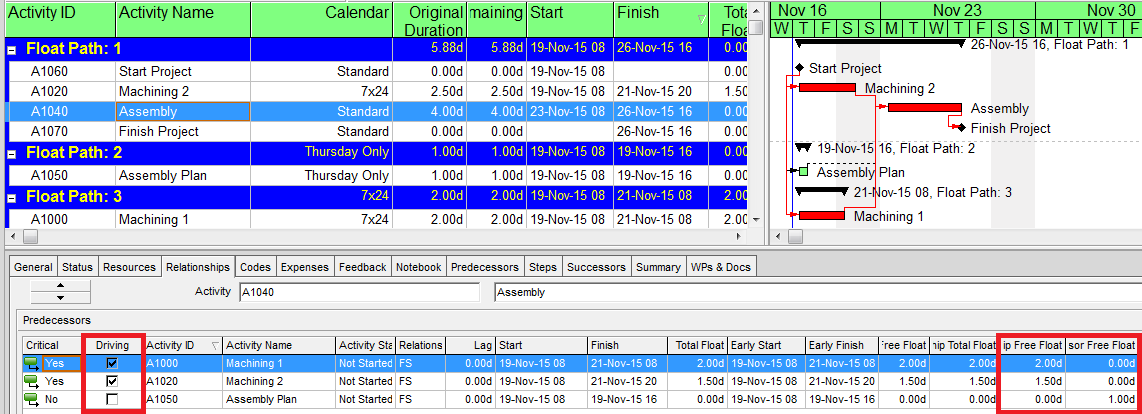
P6’s MFP algorithm (Free Float option) allocates the three predecessors of the Assembly activity to three different Float Paths:
Float Path 1 (“most critical path”): Machining 2, a driving predecessor, with Relationship Free Float (according to its own calendar) of 1.5 days.
Float Path 2 (“1st sub-critical path”): Assembly Plan, a non-driving predecessor, with Relationship Free Float (according to its own calendar) of 0.0 days.
Float Path 3 (“2nd sub-critical path”): Machining 1, a driving predecessor, with Relationship Free Float (according to its own calendar) of 2.0 days.
This is what the P6 Help file says for the MFP Free Float option.
Free Float – Choose this option to define critical float paths based on longest path. The most critical path will be identical to the critical path that is derived when you choose to define critical activities as Longest Path in the General tab. In a multicalendar project, the longest path is calculated by identifying the activities that have an early finish equal to the latest calculated early finish for the project and tracing all driving relationships for those activities back to the project start date. After the most critical path is identified, the module will calculate the remaining sub-critical paths.
Unfortunately, the underlined portion is not consistent with the observed behavior, where the Longest Path (i.e. the driving path to project completion) is divided between Float Paths 1 and 3.
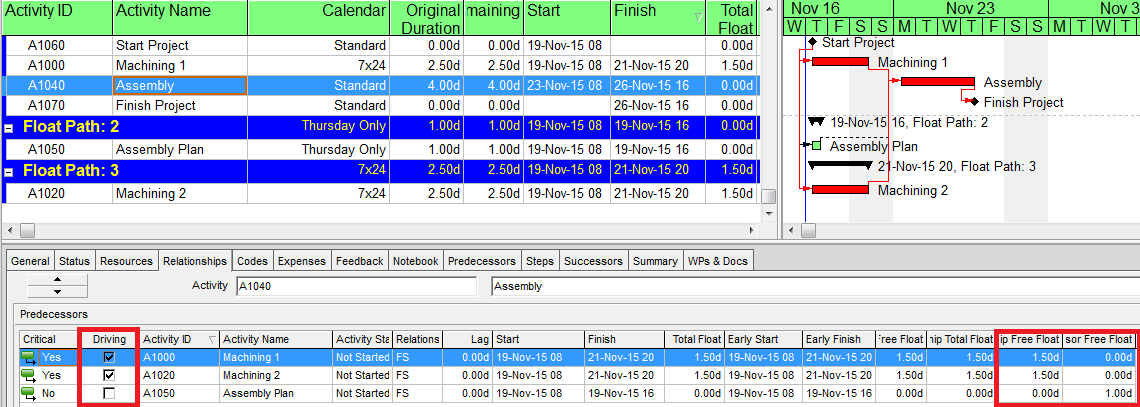
Now we modify the schedule to give both machining activities exactly the same duration (2.5 days on a 7×24 calendar), so they both finish at 8:00 PM on Saturday. They remain driving activities for Assembly and also have exactly the same Relationship Free Float (1.5d). But now they trade Float Paths: Machining 1 is now on Float Path 1, while Machining 2 is on Float Path 3.
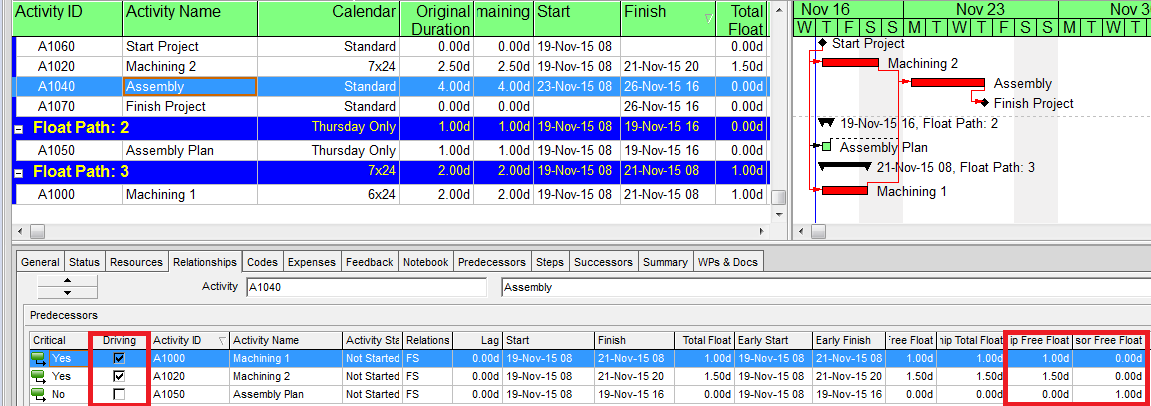
After restoring the original machining schedule (finishing 12 hours apart on Saturday), now we assign a different calendar to the one that finishes first – Machining 1 is now on a 6×24 calendar, with Sunday no longer a workday. Consequently, the Machining 1 relationship now possesses only 1.0 days of Relationship Free Float, 0.5 days less than the Machining 2 relationship. Nevertheless, Machining 2 stays on Float Path 1, while Machining 1 is still relegated to Float Path 3.
Several tentative conclusions seem apparent from these observations:
- For Float Path 1 only, the Float Path is allocated to the driving predecessor which is satisfied the latest of all the driving predecessors – without regard to Relationship Free Float. Each of the remaining predecessors will be allocated to a new (higher-numbered) Float Path.
- If two or more driving predecessors finish at exactly the same time, then only one of them – selected by Activity ID, Activity Name, or some other non-logic-related criteria [Early Start, then Activity ID according to others] – will be assigned to Float Path 1.
- For Float Paths >1, the current Float Path is allocated to the remaining predecessor (driving or not) with the lowest Relationship Free Float of all remaining predecessors. Each of the other remaining predecessors will be allocated to a new (higher-numbered) Float Path. As a consequence, legitimate members of the project’s Longest Path may be relegated to non-contiguous float paths far from the “most critical” Float Path 1. (The fact that driving predecessors are NOT prioritized is an unfortunate weakness, in my opinion, of an otherwise robust logic analysis method.)
I’ve reviewed a number of P6 schedule submittals that seem to confirm these observations in addition to a few more:
- For Float Paths >1, if the remaining predecessors are driving AND have the same Relationship Free Float, then the current Float Path is allocated to the remaining predecessor that finishes latest. Each of the other remaining predecessors will be allocated to a new (higher-numbered) Float Path.
- Consequently, in case of parallel driving paths, FF predecessors will be preferred (i.e. be allocated to lower-numbered Float Paths) over FS predecessors.
- [According to a paper first presented by Mssrs Roger Nelson and Patrick Kelly at the 2018 Annual Meeting of AACE International, and later presented at the AACE SoCal chapter meeting on 19Apr’19, the next two “tie-breakers” for path assignment are the latest Early Start date and, finally, the Activity ID.]
- In most cases, an ALAP-constrained predecessor automatically creates a parallel (and false) driving path with Relationship Free Float = 0. Extensive use of ALAP constraints can lead to a proliferation of false Float Paths in the MFP results.
[Dec’20 Note: These conclusions were tentative and reflected a relatively shallow appreciation (in July’18) of the underlying calculations. In particular, the different rules for seeding and tracing of float paths – and the consequent impact on schedules with misaligned calendars, as shown here – had not yet presented themselves. To learn more, have a look at the AACE paper and presentation noted earlier.]
See also this paper by Patrick Kelly and Roger Nelson in Cost Engineering: Primavera’s Float Path Calculation: Review and Analysis of Applications
Patrick and I followed up his earlier paper with the one discussed here:
https://boyleprojectconsulting.com/TomsBlog/2020/08/19/aace-international-annual-meeting-2020/