In a project schedule, overlapping tasks are tasks that are BOTH sequential and concurrent. The effective and efficient scheduling of overlapping tasks typically requires the use of time lags and logic relationships that are not Finish-to-Start.
Introduction
In a project schedule, overlapping tasks are tasks that are BOTH sequential and concurrent, with neither condition being absolute. They can exist in highly-detailed schedules for project engineering, design, production, and construction, though they are much more common in high-level summary schedules. Essentially, Task A and Task B are overlapping when:
- Task B is a logical successor of Task A; and
- Task B can start before Task A is finished.
Handling the second condition typically requires the use of time lags and logic relationships that are not Finish-to-Start. These elements were not supported in the original Critical Path Method (CPM), and some scheduling guidelines and specifications still prohibit or discourage their use. Nevertheless, they remain the most effective tools for accurately modeling the plan of work in many cases.
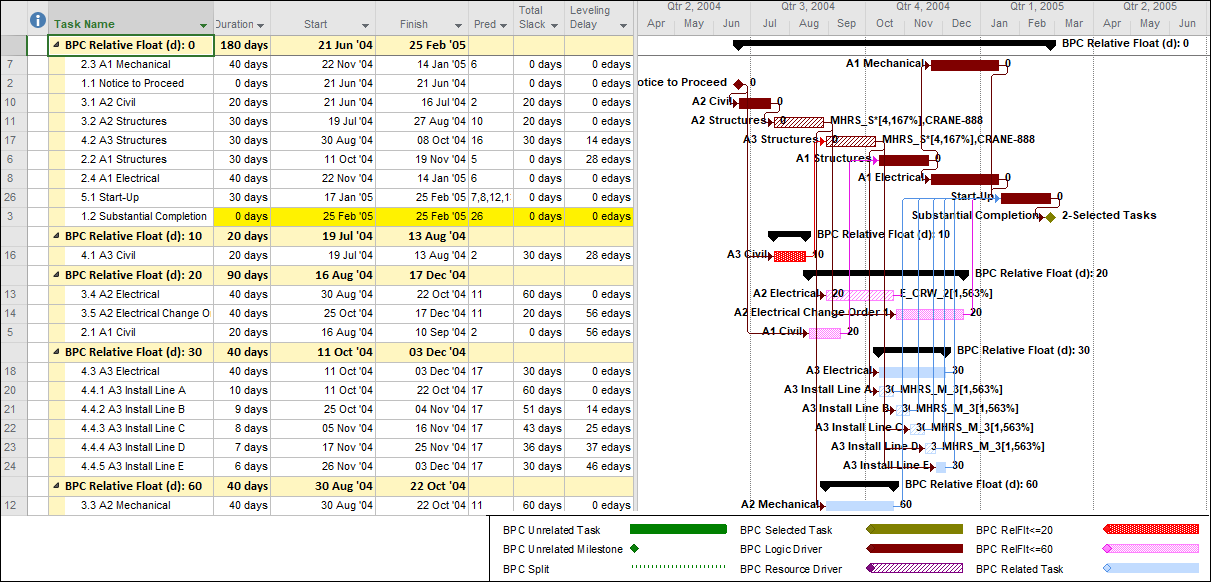
There are essentially two categories of overlapping task relationships: Finish-Start Transitions and Progressive-Feeds.
Finish to Start Transitions
Overlapping tasks with Finish-Start Transition relationships can be described in terms of a relay (foot)race, where an exchange zone for handing over the baton exists between each pair of “legs” (i.e. the 4 stages of the race). At the end of Leg 1, Runner 2 must start running before Runner 1 arrives, timing his acceleration to ensure an in-stride passing of the baton in the exchange zone, simultaneous with the completion of Leg 1. Runner 2 does not care about Runner 1’s fast start nor his awkward stumble at the midway point; his only focus is on gauging Runner 1’s finishing speed and starting his own run at the precise instant necessary to match speeds in the transition zone. In practice, Runner 2 establishes a mark on the track – paced backward from the exchange zone – and starts his own run when Runner 1 reaches the mark.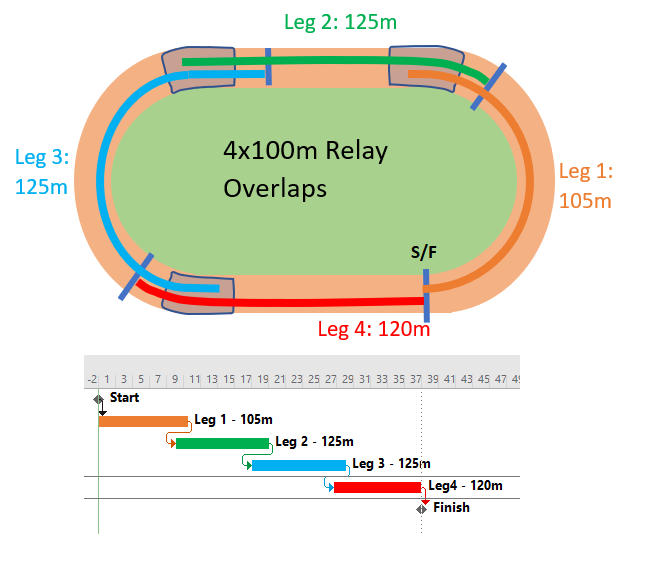
Real-world examples of such overlap include the cleanup/de-mob and mob/setup stages of sequential tasks in construction projects. In engineering/design, many follow-on tasks may be allowed to proceed after key design attributes are “frozen” at some point near the finish of the predecessor task. In general, the possibility of modest overlap exists at many Finish-Start relationships in detailed project schedules, sometimes being implemented as part of a fast-tracking exercise. The most common front-end planning occurrence of these relationship in my experience is in logic driven summary schedules, where analysis of the underlying detailed logic indicates that the start of a successor summary activity is closely associated with, but before, the approaching finish of its summary predecessor.
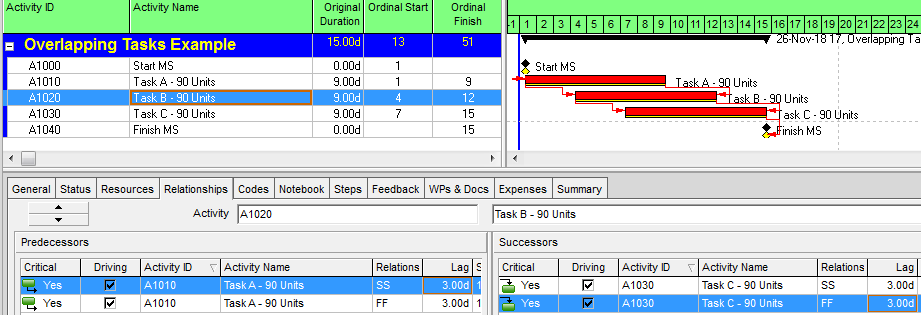
In terms of a project schedule, this kind of relationship is most easily modeled as Finish-to-Start with a negative lag (aka “lead”). This is illustrated by the simple project below, where tasks A, B, and C are sequentially performed between Start and Finish milestones. Each task has a duration of 9 days to complete 90 production-units of work. (A linear production model is shown for simplicity.) Because of the Finish-Start Transition, Task B and Task C are allowed to start 1 day before their predecessor finishes. 
Negative lags can be used for date manipulation, such as to hide an apparent delay. Negative lags can also be the source of float (and critical path) complications for project schedules with updated progress, particularly when the lag spans the data date. Consequently, negative lags are discouraged or explicitly prohibited in many schedule standards and specifications.
When negative lags are prohibited, overlapping tasks with Finish-Start transitions may be modeled by breaking the tasks into smaller, more detailed ones – all connected with simple Finish-Start links and no lags. In the example, the two negative-lag relationships can be replaced by two pairs of concurrent 1-day tasks – the last part of the predecessor and the first part of the successor – that are integrated with FS links. Thus, the overlapping linear production of the three tasks now requires 7 tasks and 8 relationships to model, rather than the original 3 tasks and 2 relationships. Alternately, each pair of concurrent tasks could be combined into a single “Transition” task, though such an approach could involve additional complication if resource loading is required.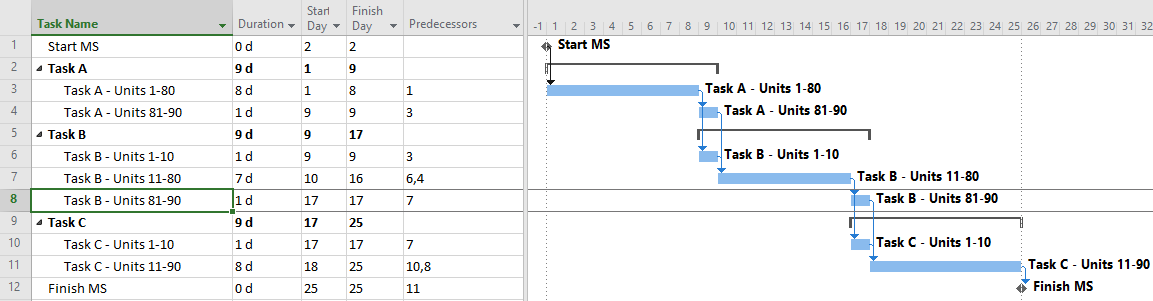
In practice, the extra detail seems hardly worth the trouble for most schedulers, so simply ignoring the overlap seems fairly common. This has the consequence of extending the schedule.
By ignoring the overlap, the scheduler here has added two days (of padding/buffer/contingency) to his overall schedule, extending the duration from 25 to 27 days. This is unlikely to be recovered.
Overlapping Tasks with Progressive Feeds
The predominant category of overlapping tasks involves repetition of sequentially-related activities over a large area, distance, or other normalized unit of production. The activities proceed largely in parallel, with the sequential relationships based on progressive feeding of workfront access or work-in-process units from predecessor to successor. In construction, a simple example might include digging 1,000 meters of trench, laying 1,000 meters of pipe in the trench, and covering the trench. The most timely and profitable approach to the work is to execute the three tasks in parallel while providing adequate work space between the three crews whose production rates are well matched. This is often described as a “linear scheduling” problem; common examples in construction are railways, roadways, pipelines, wharves, industrial facilities, and even buildings (e.g. office towers – where steel, concrete, mechanical, plumbing, electrical, finishing, and trim activities need to be repeated for each floor.) Many large-scale production/manufacturing operations are set up to maximize overall throughput by optimizing the progressive feeding of production units through the various value-adding activities. Proper scheduling of such activities is necessary when similar techniques are applied in non-manufacturing industries like construction, e.g. production lines for precast concrete piles or panels.
Below is a simple table and associated linear production chart summarizing three sequential tasks (A, B, and C) that must be repeated 90 times along a workfront to complete a specified phase of work. Each task can be executed 10 times per day, resulting in a 9-day duration for the required 90 units of production. For safety and productivity reasons, it is necessary to maintain a minimum physical separation of 30 units (i.e. 3 days’ work) between the tasks at all times. Thus, Task B must not be allowed to start until Task A has completed 30 units of production (~3 days after starting), and it must not be allowed to complete more than 60 units of production (~3 days from finishing) until Task A has finished. Task C must be similarly restrained with respect to Task B. As a result, the overall duration of the three tasks is 15 days.
The three tasks must now be incorporated into a logic-based project schedule model. When doing so, the following potential issues should be kept in mind:
- In most scheduling tools, relationship lags are based on an implied equivalence between production volume (or workfront advancement) and time spent on the task. The validity of the lags needs to be confirmed at each schedule revision or progress update. (One exception, Spider Project, may offer more valid methods.)
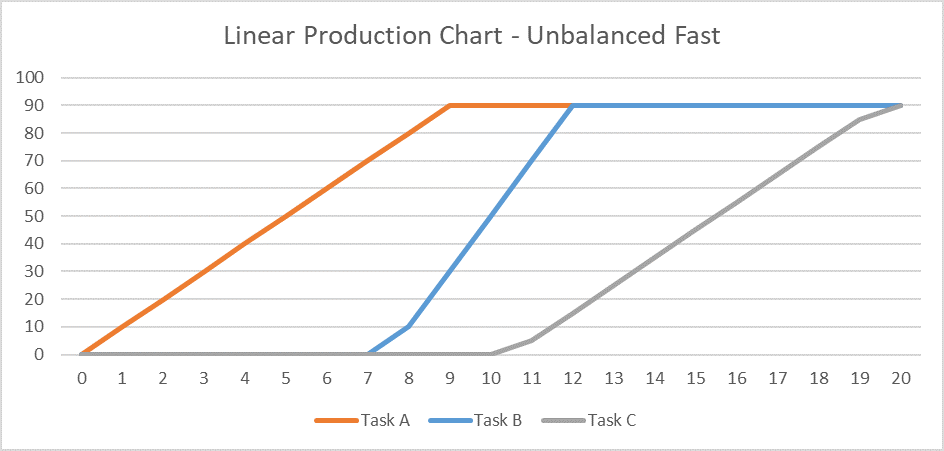
- Using progressive-feed assumptions with unbalanced production rates can have unintended consequences. For example, if the production rate of Task B is doubled such that the task can be completed in half the time, then the start of the task may be delayed to meet the finish restraint. This is consistent with a line-of-balance planning philosophy that places the highest priority on the efficient use of resources, such that scarce or expensive resources will not be deployed until there is some assurance that the work may proceed from start to finish at the optimum production rate, without interruption. In the example, the delayed start of Task B also delays the start of Task C, leading to an increase in the overall project duration from 15 days to 20 days. Some writers refer to this phenomenon as “Lag Drag.” The overall schedule is optimized when progressive-feed tasks are managed to the same balanced production rate, and disruptions are minimized.
- A progressive-feed model may not be valid if the physical or temporal requirements underlying the lags at task Start and Finish are violated during task execution. For example, if the daily production rate of Task A follows a classic S-curve profile (“Task A Logistic”) while Task B’s stays linear, then maintaining the required 30-unit minimum physical separation may require additional delay at the start of the second task.
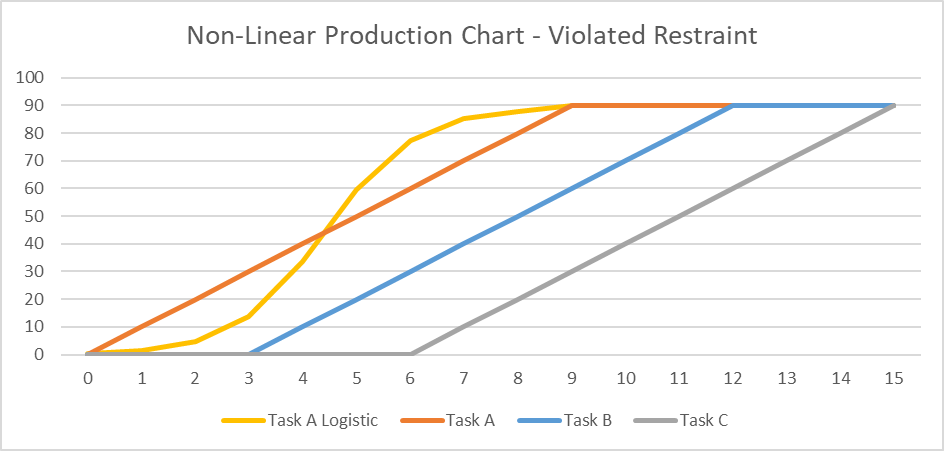
Compound Relationships: The Typical Approach in Oracle Primavera P6
As shown in the following figure, scheduling these overlapping tasks is fairly straightforward in P6. Because P6 supports multiple relationships between a single pair of tasks, it is possible to implement the required Start and Finish Separations as combined Start-Start and Finish-Finish relationships, each with a 3-day lag. These are also called “Compound Relationships.” The resulting representation of the linear schedule is completed with 3 tasks and 4 relationships (excluding the Start and Finish milestones.) The three tasks are likely well aligned with the labor and cost estimates for the project, so resource and cost loading of the schedule should be straightforward. The scheduler must still ensure that the three concerns above are addressed, namely: validating lag equivalence to work volumes or workfront advancement, balancing of production rates, and confirming lag adequacy when used with differing task production profiles.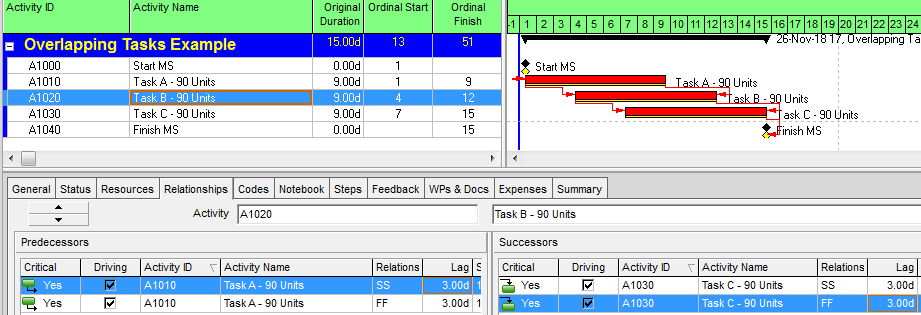
One-sided Relationships: The Typical Approach in MSP
Microsoft Project does not permit more than one relationship between any two tasks in a project schedule (see Ladder Logic in Microsoft Project). As a result, the scheduler in MSP will typically choose to implement either a Start-to-Start or Finish-to-Finish restraint with a corresponding lag. Both options are shown in the following figure.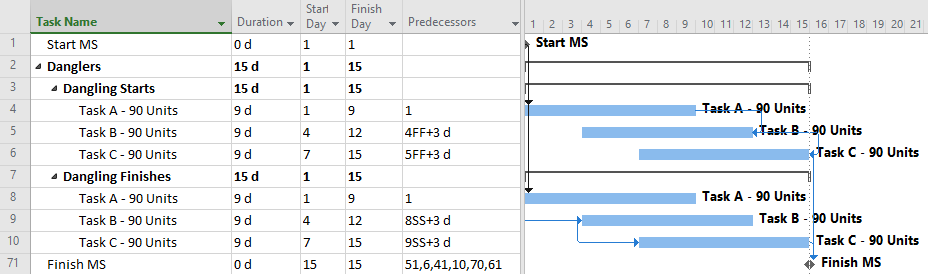
In either case, the resulting schedule will have the lowest number of tasks {3} and relationships {2} to manage (for both cost and schedule) through the project. This approach is easy to implement.
The most obvious problem with this typical approach is the inadequate logic associated with the dangling starts and dangling finishes (Dangling Logic). As a result, the typical CPM metrics of Slack (i.e. Float) and identification of the Critical Path will not be reliable, especially after the start of progress updates.
PDM with Dummy Start Milestones
Correcting the dangling logic issues in MSP schedules is most simply addressed using dummy milestones to carry either the start or finish side of the logic flow. Below I’ve shown two variations using dummy Start milestones: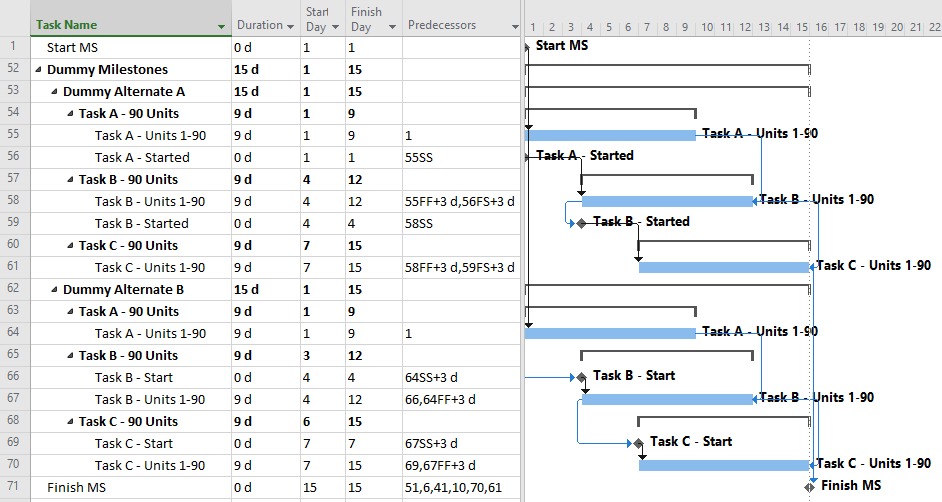
Alternate A involves trailing start milestones. Here, the milestones exist as start-to-start successors of the corresponding tasks, effectively inheriting their dates from the corresponding task start dates. The trailing start milestones pass logic to the successor tasks via relationships of the form, start-to-start-plus-lag.
Alternate B involves leading start milestones. Here the milestones exist as start-to-start successors of the preceding tasks (plus lags) and as start-to-start predecessors of their corresponding tasks (no lags).
The two alternates are largely equivalent, though Alternate B (leading start milestones) has one significant advantage: it works with percentage lags. When a percentage lag is imposed, the imposed time lag increases or decreases as the predecessor’s duration increases or decreases. This reduces some of the risks of the assumed production volume = time equivalence. (Be careful, though; the imposed lag is always a percentage of the overall Duration of the predecessor task, having nothing to do with the Actual (i.e. to-date) Duration. Moreover, all lags in MSP are imposed using the successor-task’s calendar, so mis-matched predecessor and successor calendars can bring surprises.)
Using the dummy milestones leads to valid schedule logic with a relatively modest addition of detail (i.e. medium number of tasks {5} and relationships {6}.) The schedule stays fully aligned with labor/cost estimates; no deconstruction is required, and it responds well to unbalanced and varying production rates. Unfortunately, the dummy milestones can cause visual clutter, so presentation layouts need filters to remove them from view.
Full-Detail: the CPM Ideal
Non-finish-to-start relationships were not supported in the original CPM, and they are discouraged or prohibited in some scheduling standards and specifications.
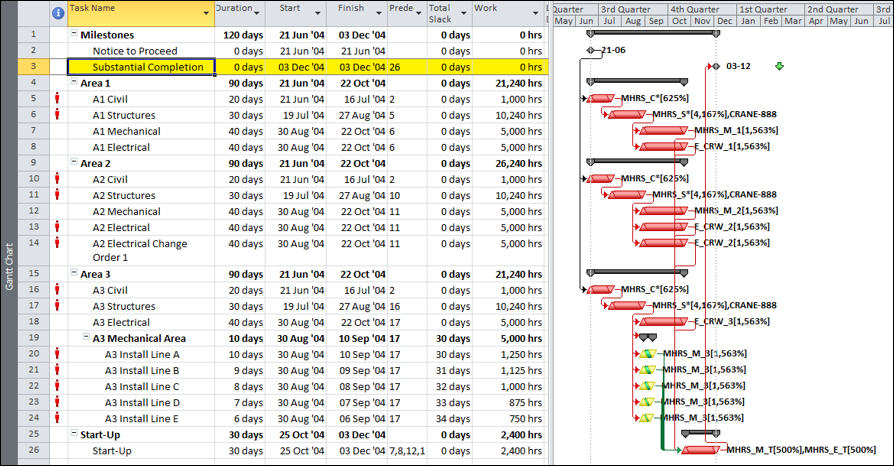
If only finish-to-start relationships are allowed, then accurate modeling of the three overlapping tasks requires substantial deconstruction into a larger number of detailed subtasks. For the three-task example, the schedule model below breaks each 9-day task into nine 1-day tasks, all integrated with finish-to-start relationships. The model is depicted using MSP; a similar model could be constructed in P6.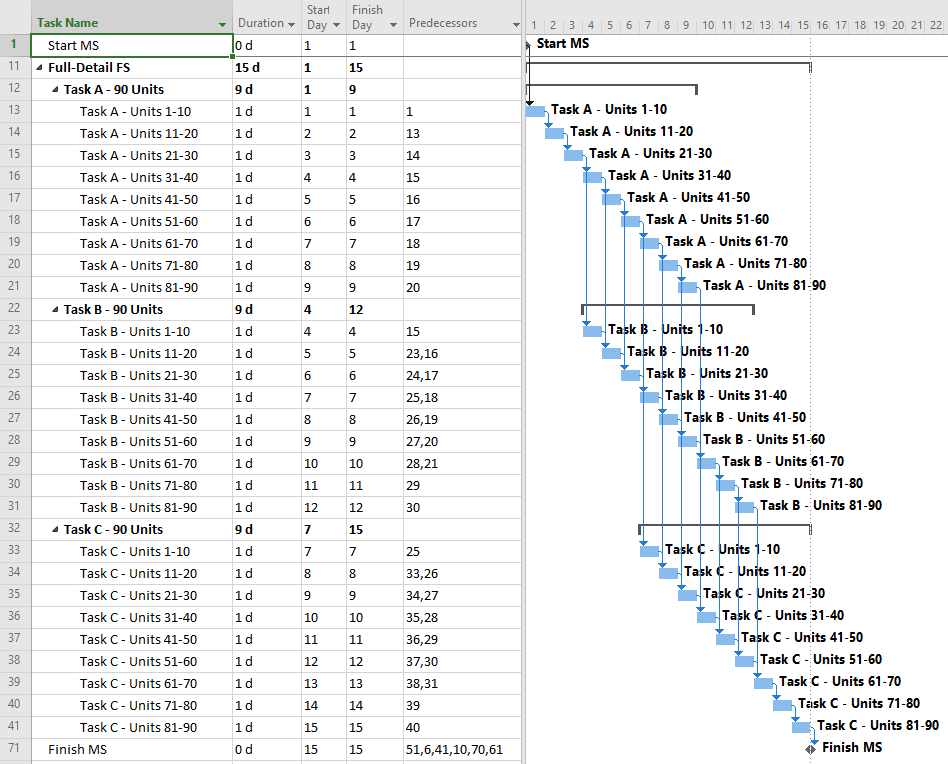
Overall, this approach appears to be more “valid” with respect to pure schedule logic. That is, there are no leads, no lags, and no non-finish-to-start relationships. The resulting model can also respond well to unbalanced and varying production rates, and it is likely to stay valid through progress updates.
On the “con” side, this model has the maximum level of detail (i.e. highest number of tasks {27} and relationships {39}.) Consequently, it will introduce substantial complications to resource and cost loading, and it will be the hardest to manage through completion. More importantly, the logic relationships that accompany such additional detail are not always technologically required. While the ordering of Units 21-30 prior to Units 31-40 may appear perfectly reasonable in the office, all that really matters is that ten units of production are received, completed, and passed on to the next task each day. The addition of such (essentially) preferential logic increases the chances that the actual work deviates substantially from the plan, as field conditions may dictate. That can severely complicate the updating of the schedule, with no corresponding value added.
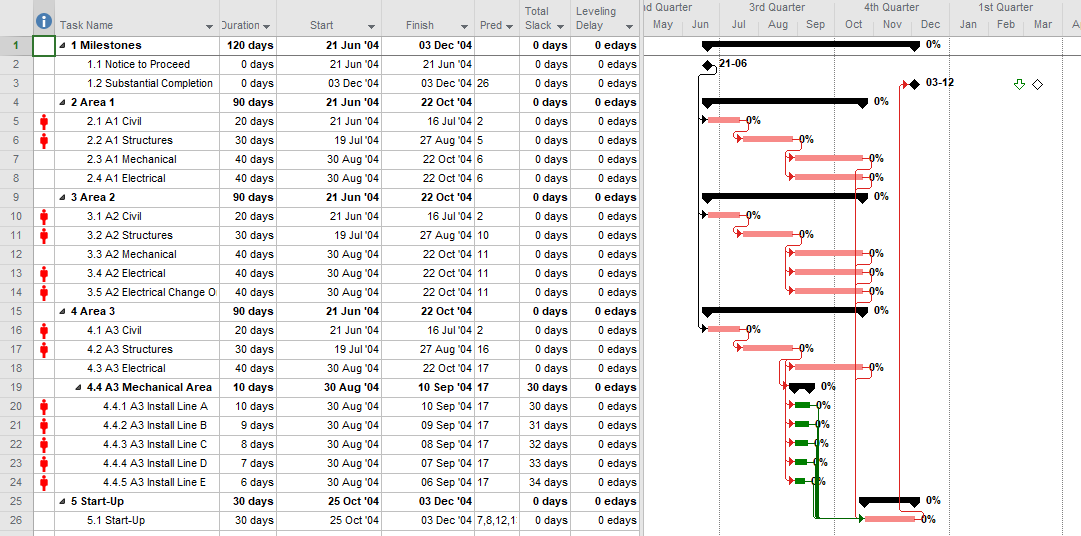
Compromise: PDM with Partial Detail
The next figure presents a compromise, providing additional task details as needed to address the initial separation requirements but minimizing the use of lags and non-finish-start relationships. The result is a moderate schedule with “mostly valid” logic and only modest level of detail (i.e. medium number of tasks {6} and relationships {7}.) Such a schedule presents medium difficulty of implementation and is less susceptible to the “preferred logic” traps identified earlier. It also responds well to unbalanced and varying production rates, and it stays valid (mostly) during progress updating.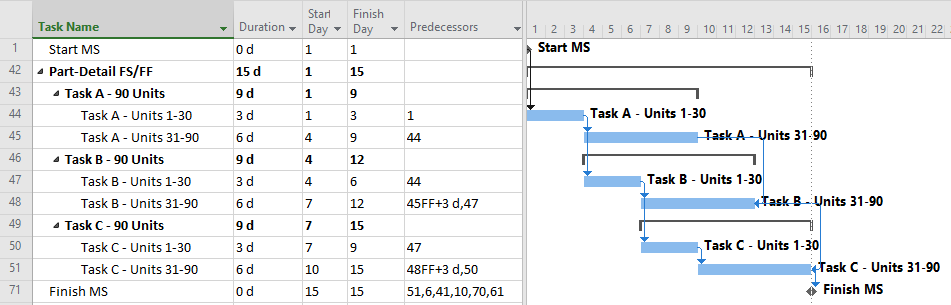
This schedule still requires consideration and validation of the progressive-feed assumptions. Since this schedule is only partly aligned with existing labor/cost estimates, some de-construction of those estimates may be required for resource and cost loading.