Multiple Float Path

Alternate Definitions of Driving Logic Relationships in Project Schedules

[Article 2 of 2.] This is a summary of the alternate definitions and uses of driving logic relationships between activities in project schedules, as applied in Primavera P6 and Microsoft Project software. Driving relationships are often considered fundamental elements of the project critical path.

This winter I worked with a colleague to prepare a paper – Interpreting Logic Paths in Multi-Calendar Project Schedules – for presentation at this year’s AACE International Conference and Expo in ~~Chicago~~ (Covid-19) virtual world. It’s a deep dive into the Multiple Float Path calculation options in Primavera P6 scheduling software. During the technical study, I had a lot of opportunities to think about driving logic relationships. I’ve summarized the standard definitions and uses in an earlier article. This entry summarizes the alternate versions of driving logic relationships that sometimes arise.

The Importance of Driving Logic

The planning and execution of complex projects requires the project team to understand, implement, and communicate the consequences of schedule logic flow to the other stakeholders. Through schedule logic, each activity in the project has the potential to constrain or disrupt numerous other activities – and to be constrained or disrupted by them. The most obvious artifacts of logic flow are the important logic paths, like the critical path, the Longest Path (in Primavera P6), or the driving path to a key delivery milestone. Regardless of the detailed definition, each of these important paths is governed by driving logic relationships from the first activity to the last activity in the path.

Late-Dates and Bi-Directional Driving Relationships in Primavera P6

From the earlier article, a relationship is considered driving (under the standard definitions) when its successor’s early dates are constrained by the relationship, during the forward pass of the CPM calculations. That is, standard driving relationships are early-dates driving relationships. A late-dates driving relationship, in contrast, is one that constrains the late dates of the predecessor, during the backward pass. When an activity has multiple successors, then one or more of these successor relationships may be controlling the late dates, and hence the total float, of the selected activity; this is a late-dates driving relationship.

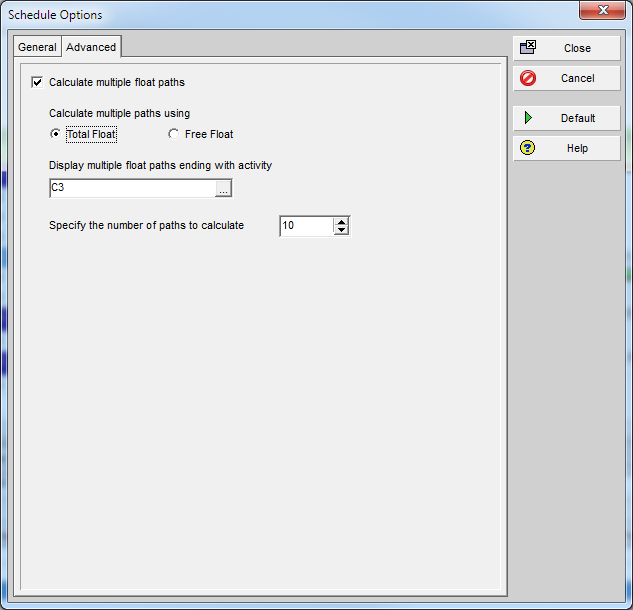
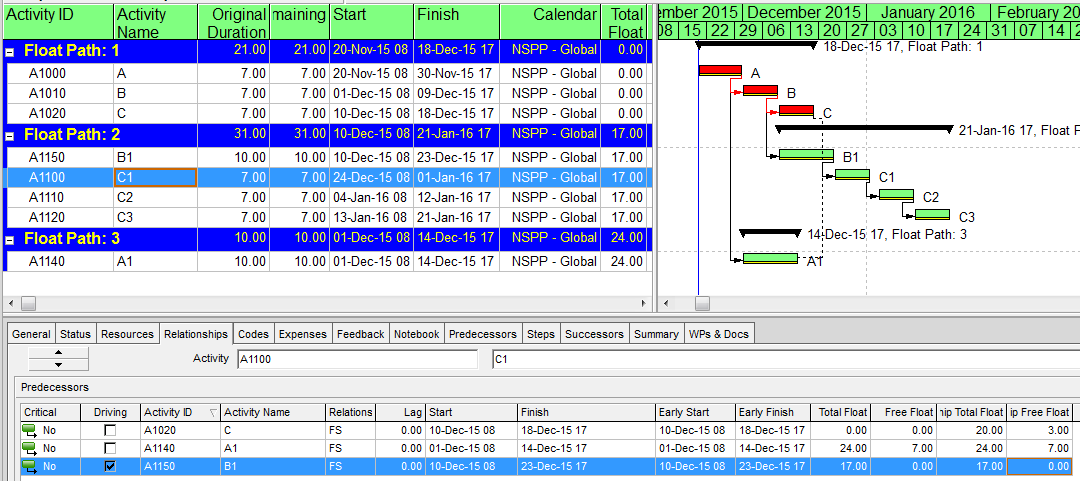
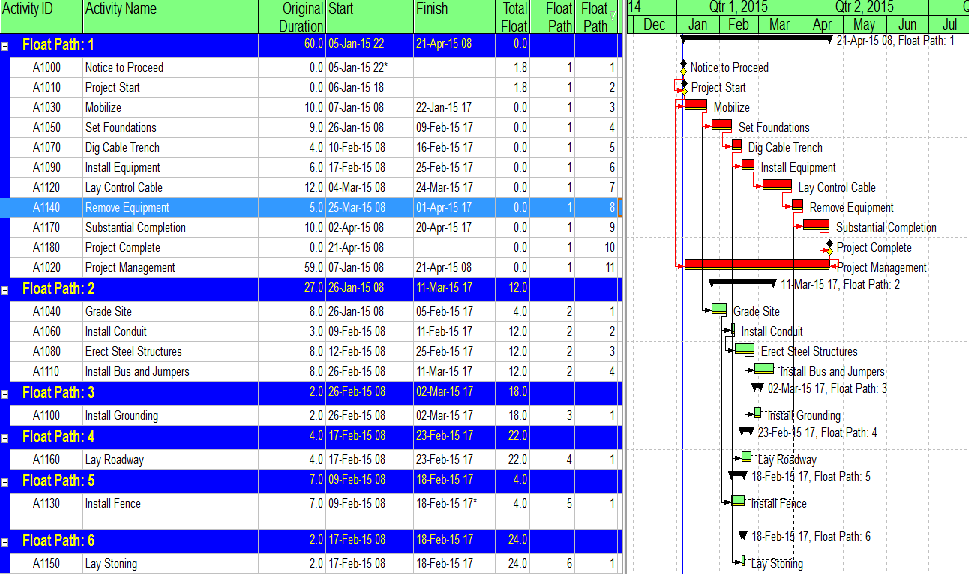
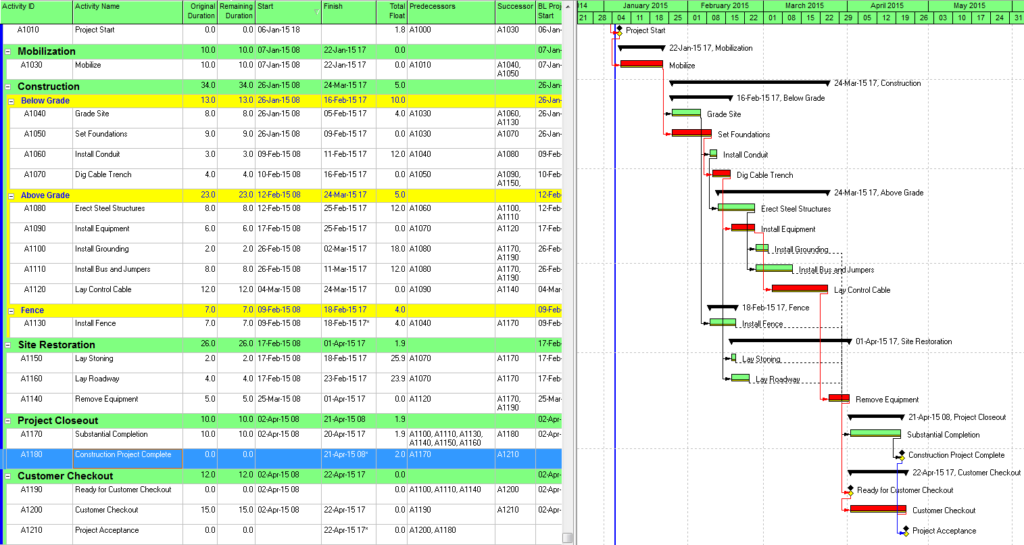
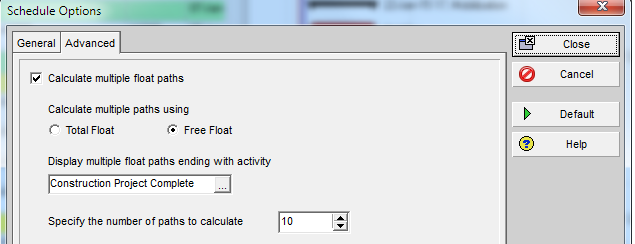
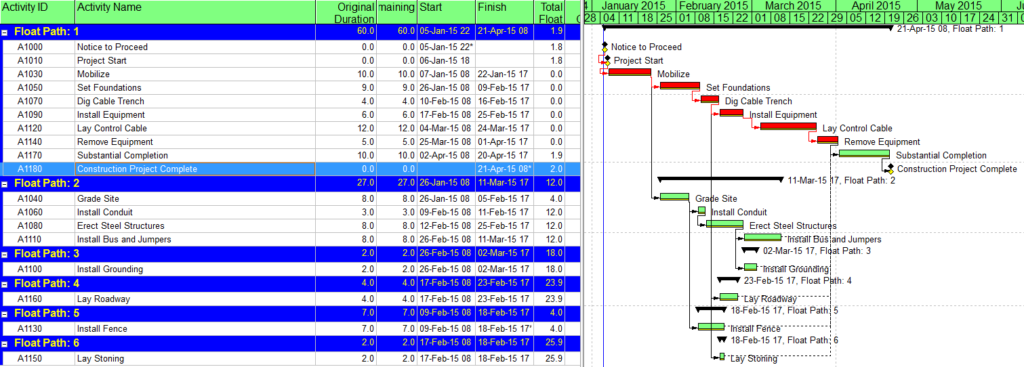
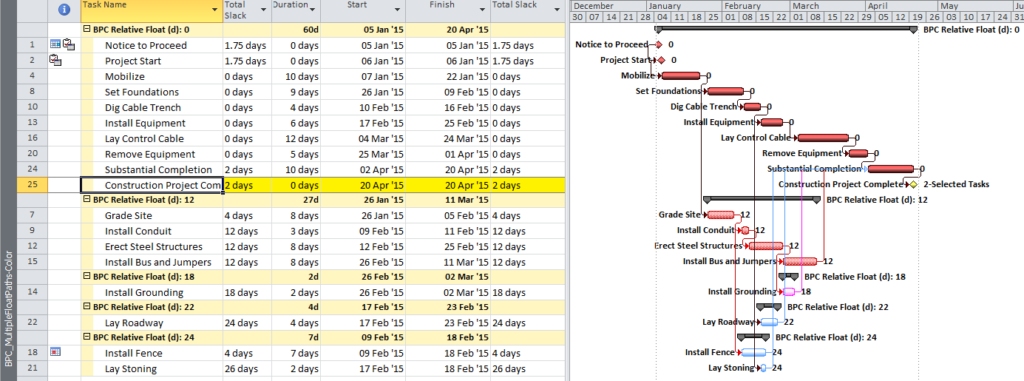
Identification of late-dates driving relationships is a key factor in P6’s Multiple Float Path (MFP) calculation. Under the total float calculation option, a relationship can be assigned to a driving “float path” only if it meets the criteria for both early-dates and late-dates driving relationships. That is, it possesses bi-directional driving logic. Since P6 does not flag or otherwise mark such relationships, the results of multiple float path calculations with the total float option can be confusing. Full understanding of the float paths may require a detailed examination of relationship and activity floats, especially when multiple calendars or constraints are involved.

For more information on MFP calculations in P6, check out these other entries in the blog:

Beyond the Critical Path – the Need for Logic Analysis of Project Schedules

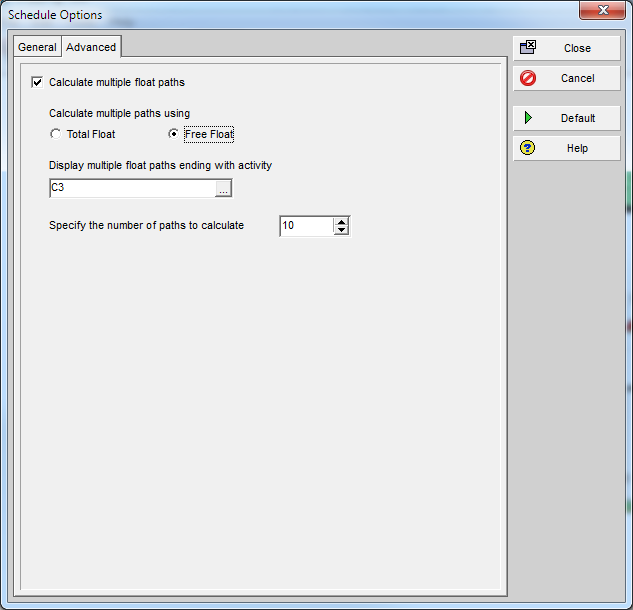
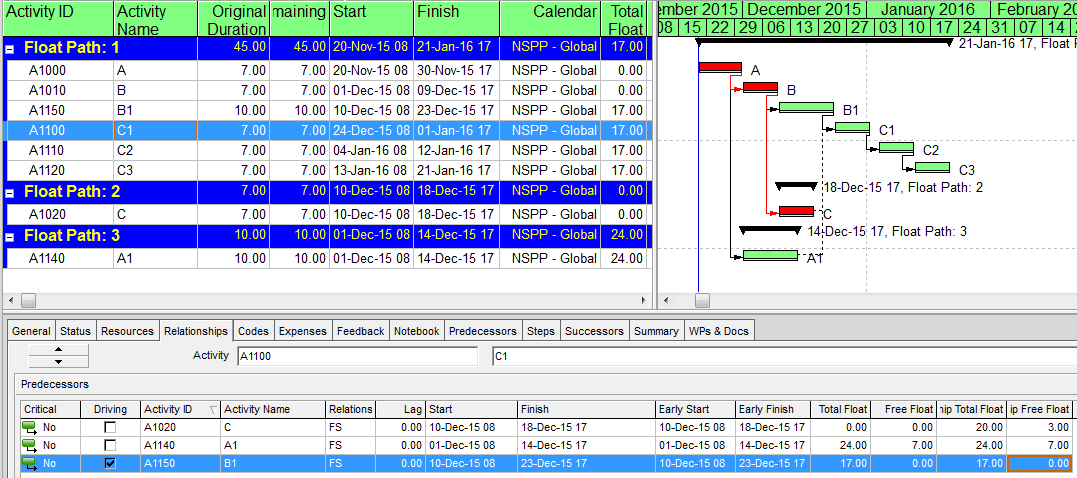
P6 Multiple Float Path Analysis – Why Use Free Float Option

Relationship Free Float and Float Paths in Multi-Calendar Projects (P6 MFP Free Float Option)

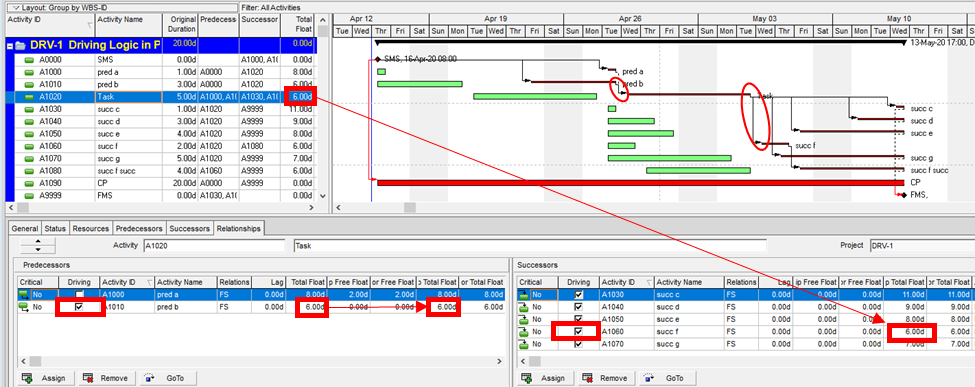
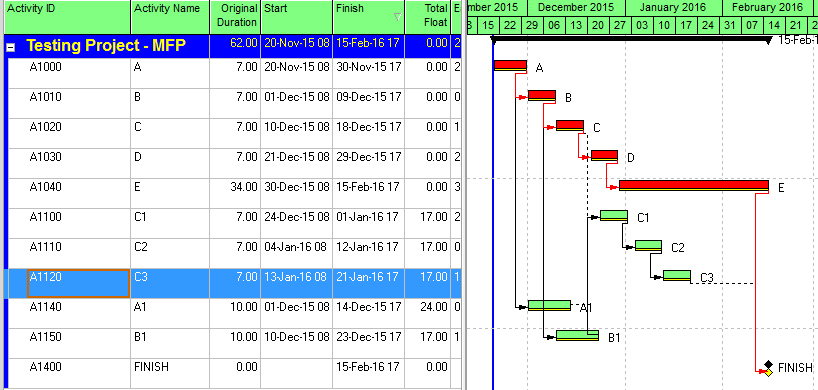
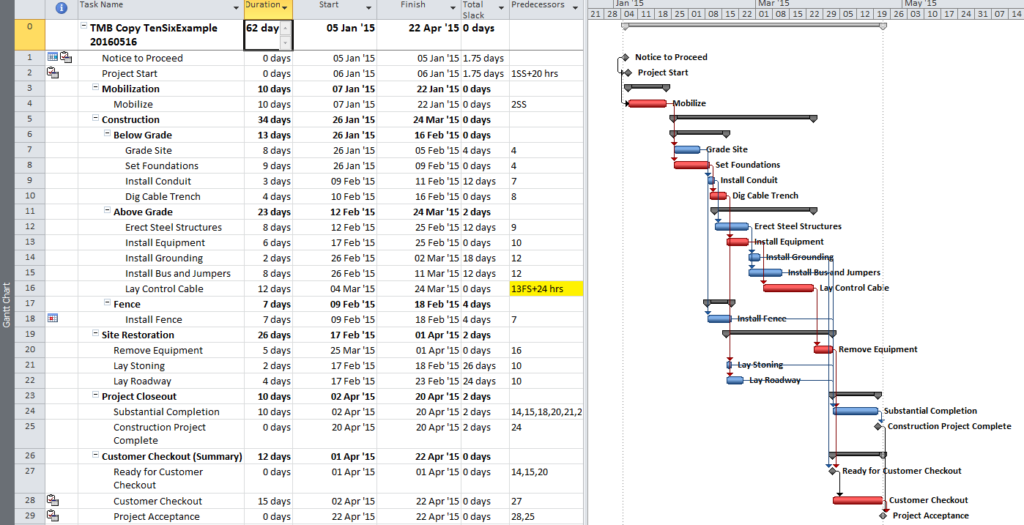
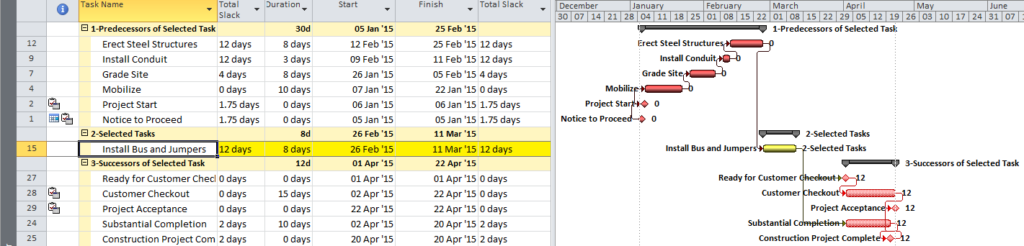
Aside from the MFP calculation option in P6, this type of driving logic is useful mainly for prioritizing driving successors when click-tracing through the schedule network in the forward direction – perhaps for schedule validation or disruption analysis. For example, consider the selected activity (A1020, “Task”) in the P6 version of our simple project below. A glance at the late-date bars shows that only one of its five driven successors (A1060, “succ f”) is responsible for the late dates (and total float) of the selected task. The corresponding relationship possesses bi-directional driving logic and marks the forward continuation of the total-float-based driving path. In the relationship tables, the “Driving” checkboxes already indicate the relationships with early-dates driving logic. When exploring forward, most P6 users will simply click to the driven successor activity that is “Critical” or has the lowest total float value, and that will be correct much of the time. When multiple constraints and/or calendars exist, however – or when the path being explored is far from critical – then late-dates driving logic is indicated when the “Relationship Total Float” equals the total float of the predecessor activity, as highlighted in the figure.

Late-Dates and Bi-Directional Driving Relationships in BPC Logic Filter

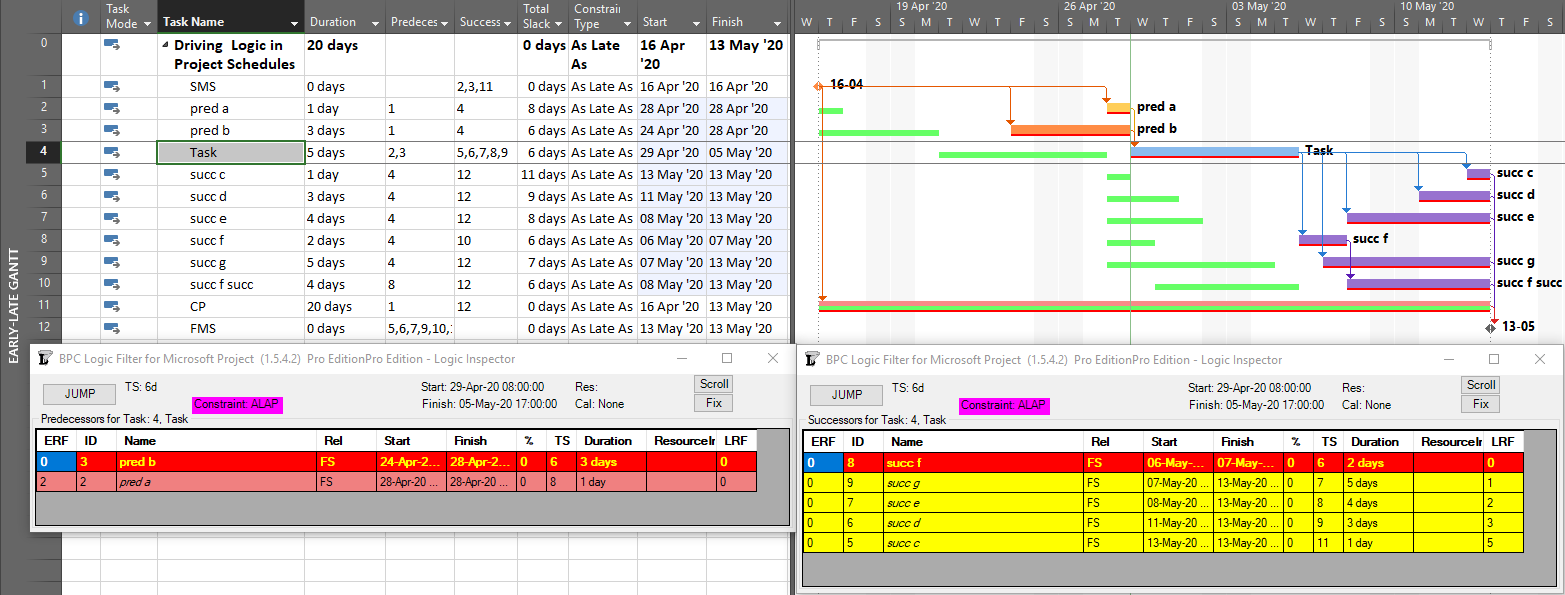
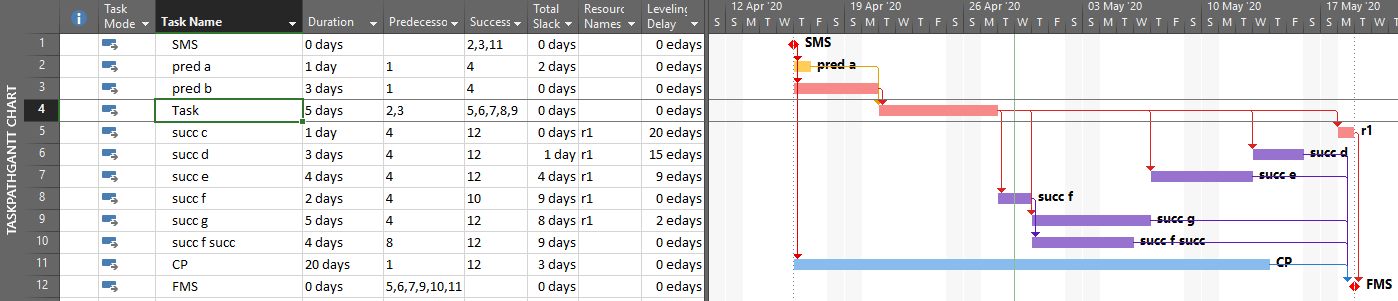
With no built-in alternatives, BPC Logic Filter automatically identify all three types of driving relationships – early-dates, late-dates, and bi-directional – in Microsoft Project schedules. The next figure repeats the same simple example project from the earlier article, with additional bars for early and late dates (green and red) and the task paths shown earlier (orange, gold, purple.) Within the logic inspector tables, bi-directional driving relationships are highlighted (red/yellow) and shown on top. Among those relationships that are NOT bi-directional drivers, early-date drivers are shown in the same yellow as before, and late-date drivers are shown in pale red. As usual, the logic inspector’s jump buttons make for easy, logic-based navigation through the schedule.

Unlike MSP’s built-in task path bar styles, the logic inspector tables are equally effective at illustrating driving logic in backward-scheduled projects. This is demonstrated below, where the same example project has been re-configured to Schedule from: Project Finish Date. Interestingly, while the scheduled dates clearly change, the nature of driving logic relationships does not.

For further information on driving logic in backward-scheduled projects, check out this earlier entry: Driving Logic in Backward Scheduled Projects (Microsoft Project), which pre-dated the introduction of late-dates driving calculations in the logic inspector.

Resource Driving Logic Relationships in BPC Logic Filter

When resource leveling is imposed in a P6 or MSP project schedule, some tasks are delayed from their CPM-based early dates until resources become available – after completion of other tasks. In the figure below, a single resource has been assigned to the five successors of the “Task,” and the resulting overallocation of the resource has been resolved by leveling the schedule using the simplest options. As a result, the project finish milestone has been delayed by three days, and the critical path has shifted.

The leveling process creates implied driving relationships between tasks that demand the same resources. BPC Logic Filter infers these “ResDrvr” relationships. As shown below, the resulting resource-constrained driving logic paths are typically very different from those identified using CPM logic alone.

The consequences of resource driving logic are further addressed in these earlier articles:

Resource Leveling Breaks the “Critical Path” – Logic Analysis of Resource-Leveled Schedules (MS Project)

The Resource Critical Path – Logic Analysis of Resource-Leveled Schedules (MS Project), Part 2

Hierarchical (Parent-Child) Driving Logic Relationships in Microsoft Project

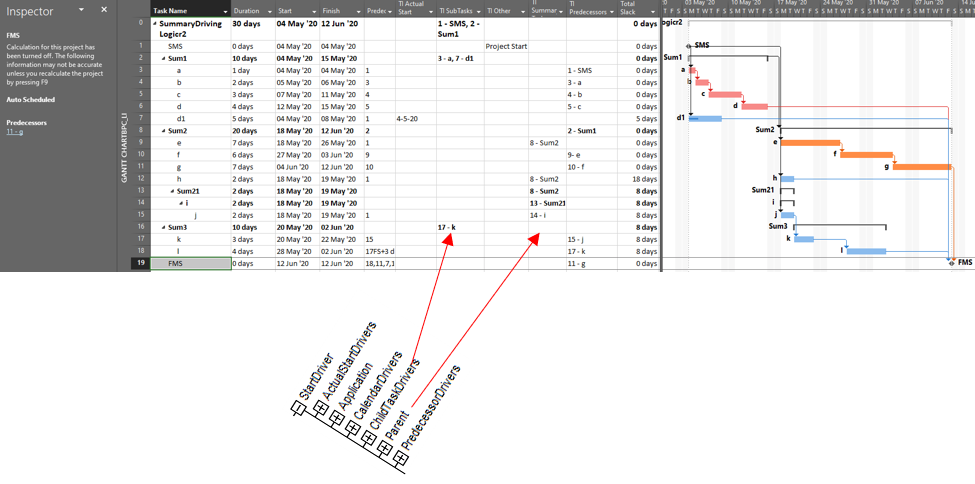
Unlike other project scheduling tools, MSP supports direct assignment of schedule logic (start predecessors and finish successors only) to “summary tasks.” As a consequence, it then imposes automatic logic restraints based on the relative positions of tasks within the Outline/Work breakdown structure. Thus, a summary task with a finish-to-start predecessor automatically imposes a corresponding early-start restraint on every one of its subtasks, and this restraint is inherited at each outline level all the way to the lowest-level subtask. Moreover, a summary task with a finish to start successor automatically imposes a corresponding late-finish (backward-pass) restraint on its subtasks, which is inherited all the way down the outline structure. External date constraints, manual-mode scheduled dates, and actual dates inputs for summary tasks have similar consequences.

The immediate early-start drivers for summary tasks and subtasks – whether a result of predecessor logic, outline-parent inheritance, or outline-child roll-up – can be identified by the task Inspector as shown in the next figure, and some of these are explicitly enumerated in the “driver” collections of the task. The late-date consequences remain implicit, however.

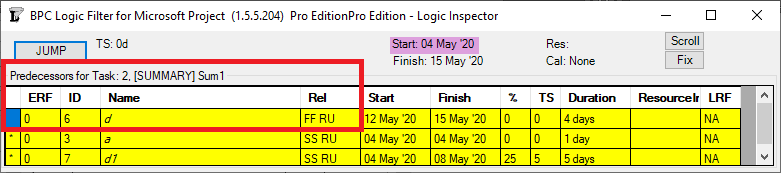
The apparent critical path for the schedule of the previous figure runs through tasks a-d and tasks e-g, including their driving FS relationships. Not shown, however, is the implicit driving FF relationship from task d to its outline parent task Sum1 (here identified in BPC’s logic inspector tool.)

The implicit driving SS relationship from task Sum2 to its outline child task e is correctly identified by the task inspector as well as BPC’s logic inspector.

Those two implicit hierarchical relationships – when combined with the explicit Sum1-to-Sum2 FS relationship – are necessary to properly calculate early and late dates and total slack, which is the source of the critical path depicted. Unfortunately, the built-in tools are not sufficient to fully trace driving logic through such hierarchical relationships, even in this simple schedule.

Neither summary-task relationships nor the consequent hierarchical (parent/child – child/parent) relationships are explicitly recognized in the generally accepted, traditional understandings of logic-based project scheduling – i.e. the critical path method (CPM) and the precedence diagramming method (PDM). Such relationships are not generally supported in other scheduling tools, either, so attempts to migrate MSP schedules containing summary logic into other tools for analysis are typically unsuccessful. It is also clear that adding even a small number of summary-task relationships to a moderately complex project schedule can potentially obfuscate the driving logic paths in the schedule, including the critical path under many circumstances, without fairly sophisticated analysis. Taking these facts together, most project scheduling professionals seem to agree that summary-task logic in MSP represents poor practice and is to be avoided.

P6 Multiple Float Path Analysis – Why Use Free Float Option

In Oracle Primavera P6, Multiple Float Path analysis is useful for identifying and organizing logic paths leading to a selected End activity in a schedule. If the Driving Logic to the End activity is desired, then the Free Float option should be selected.

When I wrote about P6’s Multiple Float Path (MFP) analysis here, I suggested using the Free Float option for identifying driving logic paths. Since then, I’ve encountered more than a few professionals who believe that the Total Float option also identifies driving logic. This entry provides a simple example illustrating why that is not always the case. [For a much more detailed review, have a look at our technical paper on interpreting logic float paths in P6.]

This “Testing Project – MFP” is a simple project that includes no constraints and only a single calendar (5dx8h). Both “Longest Path” and “Total Float” criteria lead to the same Critical Path: A-B-C-D-E-FINISH. There are several non-critical branches from the Critical Path: namely A1, B1, and C1 are successors to A, B, and C respectively. C1 is the start of the non-critical branch: C1-C2-C3. It has both A1 and B1 as predecessors, and it is driven by B1.

For this project, it is obvious (and a trivial exercise to demonstrate) that the driving logic path for any Critical Path activity is comprised of its “Critical” predecessors; i.e. those activities that are predecessors of the selected End activity and which have zero Total Float (TF=0).

What if we are primarily interested in the driving logic to an End activity that is NOT on the Critical Path – activity C3 for example? By simple inspection of the schedule (or by click-tracing from C3 backward through “driving” relationships), it is easy to see that C3’s driving logic path is comprised of the following activities: A-B-B1-C1-C2-C3. Since Total Float varies along this path (0-0-17-17-17-17), it is clear that driving logic for C3 is not associated with Total Float.

Another way to examine the logic controlling activity C3 is to re-schedule the project while calculating multiple float paths. MFP analysis examines the predecessor activities leading to a selected End activity (C3 in this case) in order of their logic sequence and assigns each of these (excluding LOE activities) to a numbered Float Path. Float Path 1 is “the most critical path.” The analysis stops when the specified number of float paths is reached. Afterward, organizing the schedule by Float Path and sorting by Float Path Order leads to a clear differentiation of logic sequence paths. I also routinely filter-out activities without float path assignment and activities with ALAP constraints. The construction of the various float paths is governed by which float option is selected – either Total Float or Free Float – in the advanced schedule options.

Total Float Option

This is what the P6 Help file says for the Total Float option.

Total Float – Choose this option to identify critical paths based on the total float of activity relationships. To calculate the most critical path, the module first determines which relationship has the most critical total float. Using this relationship as the starting point, the module determines which predecessor and successor activities have the most critical relationship total float, among all possible paths, until an activity is reached that does not have any relationships. The path that contains these activities is the most critical path.

Using the Total Float option and the other parameters shown for our simple project leads to the result shown below. Float Path 1 is limited to those activities that 1) are predecessors of C3, AND 2) have a Total Float of 0. According to P6, this is “the most critical path.” Float Path 2 is comprised of C3’s predecessors (and C3 itself) that have a Total Float of 17. Float Path 3 comprises the single logical predecessor of C3 with TF = 24. Thus, float paths appear to correspond to Total Float alone.

[Sep’19 Edit] I’ve recently read the only public foundation document for the Total Float algorithm – originally called “Enhanced” PDM in 2004 – and the observed behavior is as expected according to that algorithm. Essentially, Float Path 1 is “seeded” by whichever path-predecessor of C3 has the lowest total float (subject to some tie breakers.) Once seeded, the path is defined/traced by “bi-directional driving” relationships from the seed point. A “bi-directional driving” relationship exists when:

The Relationship Total Float equals the total float of the predecessor activity; AND
Relationship Successor Free Float = 0. (P6 support docs point to the “most critical” Relationship Successor Total Float here, but that didn’t stand up to close scrutiny.)

Subsequent float paths are seeded and traced using the same priorities.

Fundamentally, the algorithm was developed to a) differentiate float-based critical paths and near-critical paths in the presence of multiple calendars; and b) differentiate independent driving logic paths, including multiple critical paths, that share the same total float. So here in the absence of calendars or parallel critical paths, the alignment of the calculated float paths and total float is exactly as expected.

Clearly, none of the 3 float paths from the Total Float option correspond to the actual Driving Path to activity C3. Path 1 includes activity C, which although it is on the Project’s Critical Path is NOT on the Driving Path to activity C3. The actual Driving Path has been split between Float Path 1 and Float Path 2.

Thus, using Total Float option, Float Path 1 – “the most critical path” – comprises those activities that are predecessors of activity C3 and have the lowest total float. C3’s own driving/controlling logic path is not defined by the float paths assigned.

Free Float Option

This is what the P6 Help file says for the Free Float option.

Free Float – Choose this option to define critical float paths based on longest path. The most critical path will be identical to the critical path that is derived when you choose to define critical activities as Longest Path in the General tab. In a multicalendar project, the longest path is calculated by identifying the activities that have an early finish equal to the latest calculated early finish for the project and tracing all driving relationships for those activities back to the project start date. After the most critical path is identified, the module will calculate the remaining sub-critical paths.

Using the Free Float option and the other parameters shown for our simple project leads to the result shown below. Float Path 1 exactly corresponds to the known Driving Path to activity C3: i.e. A-B-B1-C1-C2-C3. Float Path 2 is comprised of activity C only, while Float Path 3 is comprised of activity A1 only. Float paths clearly have no correspondence to Total Float.

The key decision point in allocating float paths seems to occur at the predecessors to activity C1: i.e. C, A1, and B1.

C has an activity Total Float of 0. The C-C1 relationship has a Relationship Total Float of 20 and a Relationship Free Float of 3.
A1 has an activity Total Float of 24. The A1-C1 relationship has a Relationship Total Float of 24 and a Relationship Free Float of 7.
B1 has an activity Total Float of 17. The B1-C1 relationship has a Relationship Total Float of 17 and a Relationship Free Float of 0.

Although the Help file is essentially silent on the issue, the MFP analysis appears to allocate these predecessor activities to the three float paths on a basis that correlates to Relationship Free Float. Here, a Relationship Free Float of zero indicates a Driving Relationship. Successively higher values of relationship free float correspond to less-driving relationships and result in assignment to higher-numbered float paths.

Thus, using Free Float option, Float Path 1 – “the most critical path” – comprises the driving path to the selected end activity. Higher-numbered float paths correspond to “sub-critical” paths, or to successively less-driving paths to the selected end activity.

[Jul’18 Amendment – Unfortunately, the ordering of these “sub-critical” paths can be counter-intuitive, with true “Longest Path” activities sometimes being relegated to high-numbered float paths. See Relationship Free Float and Float Paths in Multi-Calendar Projects (P6 MFP Free Float Option).]

Significance of Total Float

The “Critical Path” of a logic driven project schedule is the collection of activities that determine the earliest possible completion date of the project – i.e. the driving logic path to project completion. In the original Critical Path Method and its variants, the Critical Path was reliably correlated to a Total Float value of zero, and delay (or acceleration) of any Critical Path activity cascaded directly to the project completion milestone. Near-critical paths were defined by successively higher values of Total Float. In simple projects, therefore, Total Float is a reliable indicator of the logical association between any given activity and the project’s Completion.

Because of Total Float’s significance in the traditional definition of Critical and Near-Critical Paths, it is easy – but generally incorrect – to presume a logical association between two activities on the basis of their Total Float values. In the absence of any late constraints, multiple calendars, or resource leveling, then such associations may exist between certain critical or lower-float successors and their higher-float predecessors. Thus, running MFP analysis using the Total Float option may be expected to reveal driving and near-driving logic when the selected End activity is on the float-defined Critical Path. As shown in the example above, however, such an analysis does not reveal driving and near-driving logic when the selected End activity is not Critical.

When a project schedule includes multiple calendars, resource leveling, or a late constraint on any activity except the final one, then Total Float becomes unreliable for indicating the driving path to project completion. Similarly, it becomes less useful for identifying driving and near-driving logic paths to selected activities even when they are on the “Critical Path”. In projects with multiple calendars and modest progress updates, the float paths defined using the Total Float option can deviate substantially from both the known driving paths and simple Total Float-based paths. Under these conditions, the Free Float option is almost certain to provide a clearer view of the schedule logic driving an activity, regardless of its criticality.

Beyond the Critical Path – the Need for Logic Analysis of Project Schedules

This entry is intended to review the use of the Multiple Float-Path calculation option in Primavera Project Management (P6) and to offer a brief example of its use compared to BPC Logic Filter (for Microsoft Project).

Project schedules generated using the Critical Path Method (CPM) are commonly used to model – and to document – the project team’s plan for executing the scope of work. Such a plan normally involves identifying necessary activities at an appropriate level of detail and specifying the necessary sequential relationships between them. The output from the CPM analysis is a list of activities with associated durations, dates, and float values – this constitutes “the schedule”.

Unfortunately, the sequential relationships that ultimately drive the schedule (i.e. the logical “plan”) can be difficult to communicate or analyze for all but the simplest projects. This is because Total Float – the telltale indicator of logical-path connectivity in simple projects – becomes unreliable (or unintelligible) for such purposes in the presence of variable activity calendars or late constraints. As a result, complex schedule models lose both usefulness and credibility among project stakeholders unless schedule managers go beyond the simple communication of dates, durations, and float.

Multiple Float Paths

Oracle’s Primavera P6 software (P6) has always included an option to compute “Multiple Float Paths” when calculating the schedule, but many experienced planners seem unfamiliar with it. The option facilitates the identification of the “driving” and “near-driving” logical paths for a single selected activity. The selected activity can be a key project milestone that may or may not correspond to the end of the project, or it may be a simple intermediate activity of particular or urgent concern.

Figure 1 represents a simple project for construction and handover of a small utility installation – originally modeled in Microsoft Project and then converted to Primavera P6. (The model was developed primarily for illustrating the impact of calendars and constraints; the work techniques illustrated are neither typical nor ideal.)

There are contractually-derived late-finish constraints on the Construction Project Complete milestone (24Apr’15) and the final Project Acceptance milestone (29Apr’15). These constraints affect the late dates (and consequently Total Float) for these activities and (parts of) their chains of predecessors.
There is a late-finish constraint (25Feb’15) on the “Install Fence” activity (reason not known), with similar impacts on late dates and Total Float.
Activities are scheduled using a 4d x 8h work week (M-Th), except for the two initial milestones which utilize a 24-hour calendar, and the final two Customer Checkout activies which utilize a 5d x 8h workweek.
The “Notice to Proceed” milestone is constrained to start no earlier than 10:00 PM on 05Jan’15.
P6’s scheduling options are set to define critical path activities on the basis of “Longest Path” rather than Total Float, and the Gantt chart appears to properly display the Critical Path by this definition. Thus, the two initial milestones are marked as critical because they are driving the project’s completion, even though their calendars allow a higher value for total float.

Figure 1: (P6) Simple Construction/Handover Project

Although “Longest Path” appears to correctly identify the driving path to the project completion (the Project Acceptance milestone), the contractor is equally interested in identifying the driving path to the “Construction Project Complete” intermediate milestone.

In P6’s advanced schedule options, we select “calculate multiple float paths” ending with the “Construction Project Complete” milestone” (Figure 2). As a rule, we calculate the multiple paths using “free float” rather than “total float”, since the former option best mimics “longest path” behavior.* The default number of paths to calculate is ten.

* See “P6-multiple-float-path-analysis-total-float-and-free-float-options” for more on these options.

Figure 2: (P6) Schedule Option for Multiple Float Paths

Figure 3 illustrates the result of re-calculating the schedule then displaying a layout that arranges the activities by “Float Path” and sorting by “Float Path Order”. In this figure, “Float Path 1” is the driving logical path leading to the Construction Project Complete milestone. “Float Path 2” defines the first near-driving-path, “Float Path 3” defines the next near-driving path, etc. Each “float path” is essentially a discrete branch from the main, driving logical path. Obviously, Float Path 1 defines the activities that offer the most opportunity to accelerate the construction project (and maybe the most risk of extending it.) According to the figure, higher float paths tend to have higher values of total float, though the correlation is not universal.

Figure 3: (P6) Multiple Float Paths to Interim Milestone

Unfortunately, P6 does not rigidly distinguish between driving-paths and near-driving paths. That is, while float path 1 is always “the” driving path, float path 2 may designate another, parallel driving path or a path that is 2 days from the driving path. It is not obvious how far a certain numbered path may be from driving; that is, what is its “relative float” with respect to the end activity? You can try to estimate this manually by looking at start and finish dates of various related activities in the output. More rigorously, the relative float of each path can be computed by summing the “Relationship Free Float” of all the relationships between the given path and the end activity. [Jul’18 Edit: In certain cases P6’s path-selection criteria can relegate parallel driving-path activities – even Longest-Path activities – to high-numbered float paths that appear far from the driving path. I described this in a later article – Relationship Free Float and Float Paths in Multi-Calendar Projects (P6 MFP Free Float Option).]

Ongoing management of projects often requires what-if analysis of prospective disruptions, and P6’s MFP can be useful. For example, the subcontractor for the “Install Bus and Jumpers” activity may request early access to accommodate a staffing conflict. Running MFP ending with “Install Bus and Jumpers” will identify the driving path of predecessors for this work (Figure 4), assisting in the review and consideration of the request.

Blog151226Fig4 — Figure 4: (P6) Multiple Float Path to Install Bus and Jumpers

Figure 4 demonstrates the utter lack of correlation between Total Float and the driving logical path for any given activity in the schedule.

A Word about LOE Activities and ALAP Constraints (P6)

Depending on the scheduled dates, P6 automatically sets the relationships of LOE (level-of-effort) activities to “Driving”. As a consequence, P6’s Longest Path algorithm traces driving flags directly through LOE activities to their non-critical predecessors, and these end up – incorrectly – on the Longest Path. Fortunately, this error seems to be avoided in Multiple-Float Path analysis. MFP tracing correctly identifies only true driving logic and excludes LOE activities from the trace. (I’ve illustrated this in another entry HERE.)

Like LOEs, predecessor relationships from activities with ALAP (as-late-as-possible) constraints in P6 can be flagged as “Driving” based on their dates alone. Consequently, each ALAP-constrained predecessor creates a new parallel driving path to the selected end activity, and these paths are mapped in the MFP analysis. Since ALAP-constrained activities are rarely actually driving anything, it can be useful to filter them out from standard MFP layouts.

Multiple Float Path Analysis in Microsoft Project

(Microsoft Project provides neither Longest-Path nor Multiple-Float-Path analysis. BPC Logic Filter is an add-in that applies similar calculations to MSP schedules.) Figure 5, Figure 6, and Figure 7 illustrate the same steps as above, but this time executed on the Microsoft Project version of the schedule using BPC Logic Filter. In this type of analysis, the primary difference between P6 and BPC Logic Filter is that BPC Logic Filter explicitly computes and displays “Relative Float” (i.e. days away from driving) for each path. Thus two logical paths with the same relative float (i.e. parallel paths) are grouped together in BPC Logic Filter, while P6 assigns separate float paths. The MSP add-in also re-colors Gantt bars based on their path relative float with respect to the “selected” task.

Figure 5: (MSP) Simple Construction/Handover Project

Figure 6: (MSP) BPC Logic Filter – Multiple Float Paths to Interim Milestone

Figure 7: (MSP) BPC Logic Filter – Driving Path to Install Bus and Jumpers

Finally, BPC Logic Filter allows a more substantial evaluation of the upstream and downstream logic affected by the potential change to “Install Bus and Jumpers”. Figure 8 identifies the predecessor and successor paths for the selected task, all arranged according to their path relative float (shown at the end of each bar) with respect to the selected task. This illustrates that, while the selected work cannot be accelerated without violating (or modifying) its driving predecessor logic, it may be delayed by up to 12 days without affecting any successor work.

Figure 8: (MSP) BPC Logic Filter – Driving and Driven Paths for Intermediate Activity (Install Bus and Jumpers)

As a long-time Primavera user accustomed to MFP analysis options, I was continually disappointed when faced with the need for logical path analysis in Microsoft Project. I wrote BPC Logic Filter in part to cover this gap; now I find myself facing disappointment in the opposite direction.