In complex project schedules, multiple critical paths can exist between the project’s start and finish milestones. Additionally, integrated projects with multiple phased scopes of delivery often have several distinct, contractually-mandated deliverables and corresponding delivery dates. Each possesses its own critical/driving path.
[Note to searchers: This article has a slight mention of Microsoft Project’s Advanced Calculation Option – “Calculate Multiple Critical Paths.” It’s near the end, in the section called A Note About Open Ends.]
A key tenet of the original Critical Path Method (CPM) of project scheduling is that each project has one and only one “Critical Path” (CP) that extends continuously from the project start milestone to the project finish milestone. The CP is defined by the collection of activities that determine the finish date of the project, such that a delay of any one of them will delay the project. Traditional methods identify the CP based on Total Slack/Float. For an elementary review, have a look at The Ultimate Guide to the Critical Path Method over at projectmanager.com.
[As demonstrated in this heavier article of mine, the CP is in many cases not actually defined by the collection of “Critical” activities from the software.]
Single Finish Milestone w/ Parallel Drivers
It is possible for the “critical path” between the start milestone and the finish milestone to have several parallel branches of equivalent length. These can be described as “multiple critical paths.”
Depending on the details of the schedule model, it is not uncommon to have at least a few activities that are both concurrent and critical. That is, they comprise parallel branches of a common logic path that drives the completion of the project. For example, the construction schedule for a residential building may include one activity for “plumbing rough-ins” and another activity for “electrical rough-ins” (where “rough-in” is another term for “first fix” work.) The two activities have the same driving predecessors (e.g. structural framing) and driven successors (e.g. wall finishes), and they take the same amount of time to complete. If the wall finishes are on the driving path to project completion, then the two rough-in activities form parallel branches of the “Critical Path” for the project. Such parallel branches might be repeated for each floor of a multi-story building. In practice, instances of parallelism/concurrency that comprise only a few activities like those described here seem rarely, if ever, to be identified as “multiple critical paths.” This is because a) the parallel activities are seen as closely related; and b)traditional methods of identifying and depicting critical activities do not differentiate between the associated logic paths, typically sorting by dates and filtering primarily on the software’s “critical” flag and/or Total Slack/Float.
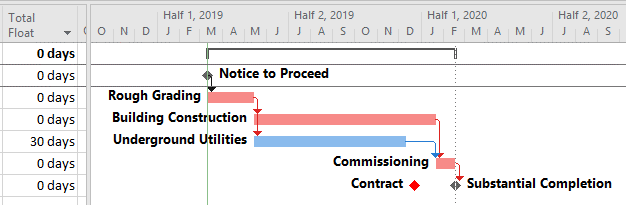
Multiple critical paths are also created by efforts to accelerate the project completion, such as crashing or fast-tracking exercises, after the initial development of the schedule. For example, a large scale construction project must be accelerated by 40 days to meet contract commitments. The critical path of the initial project schedule runs through building construction, while underground utility development activities possess 30 days of Total Float.
Additional resources (and costs) may be applied to compress the building construction activities by 30 days and yield a corresponding acceleration of the project completion. At that point, the building construction and utility development activities must both be compressed by an additional 10 days (and at additional cost) to obtain the necessary 40-day acceleration of the project. After the exercise, the building construction and utility development activities are equally driving the project completion, and the schedule possesses two critical paths.
Further crashing or fast-tracking exercises may add more critical paths. The associated activities all possess the same total float/slack, and all are marked as “critical.” Differentiating between the various paths requires a method for separately tracing and coding driving logic, either analytically or by visual inspection. Such methods are explored later in this article.
In practice, multiple critical paths are also created during project execution, as float is completely consumed by unplanned delays in activities that were previously non-critical. Exploration of such delays will have to wait for another article. (Notions of the “Critical Path” are sometimes suspended in the late stages of major/mega projects, as virtually every incomplete activity may delay the ultimate completion of the project and is therefore “Critical”.)
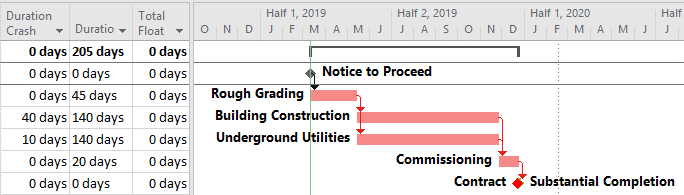
Ultimately, all three of these instances of multiple critical paths can be traced to a certain simplification (or presumed simplification) of resource utilization in the project. In the first example, plumbing and electrical crews are presumed to have exactly the same productivity, resulting in the same duration for both activities. In fact, one of the crews may be capable of completing the work sooner but paces its effort in order to match the scheduled duration. In the second example, it is presumed that the building construction activities and utility development activities may be compressed by exactly 40 days and 10 days, respectively. In fact, optimum resource usage often follows a step-wise rather than linear (or even continuous) function; consistent with adding discrete crews or substituting higher-capacity equipment. Thus, the building construction may be optimally compressed by 35 days or 45 days (not 40 days), and the utility development may be optimally compressed by 9 days or 12 days (not 10 days). As a result, the project completion is optimally accelerated by 42 days (not 40 days), with the critical path being governed by utility development. The crashed building construction activities get 3 days of float. 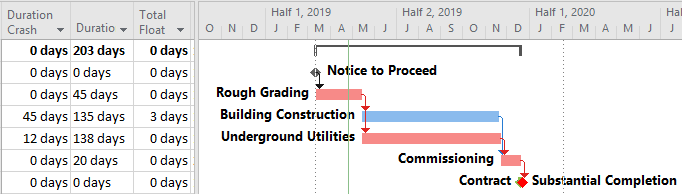
When taken to this level of detail, a single critical path may indeed be re-established. Depending on the needs of the project, such detail may or may not be justified in light of various project uncertainties and the increased management effort involved.
Multiple Delivery Milestones
When a project involves the parallel or interim delivery of multiple scopes of work, each delivery may be construed to have its own “critical path” – i.e. the sequence of activities and relationships determining the delivery date for the particular scope of work. More importantly, any particular activity in the project schedule may be expected to participate in more than one of these multiple critical paths. Examples include design, setup, or testing activities that may be common to several deliveries.
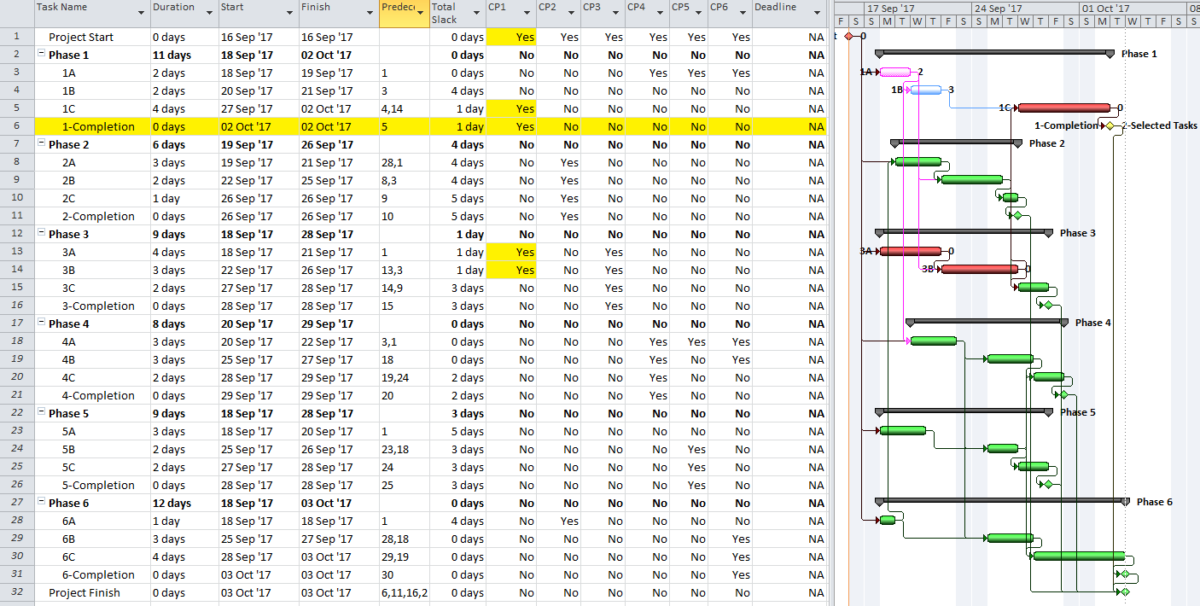
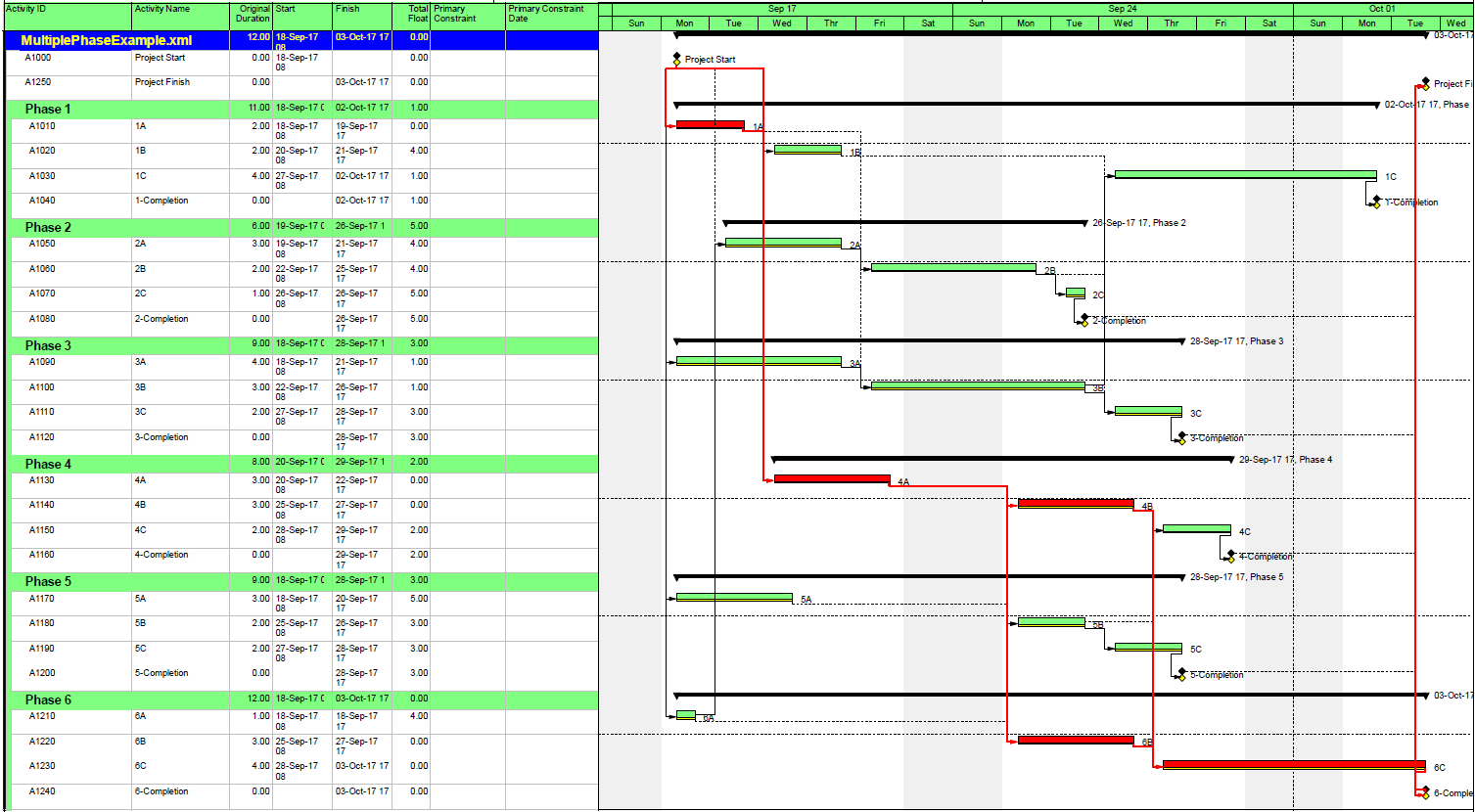
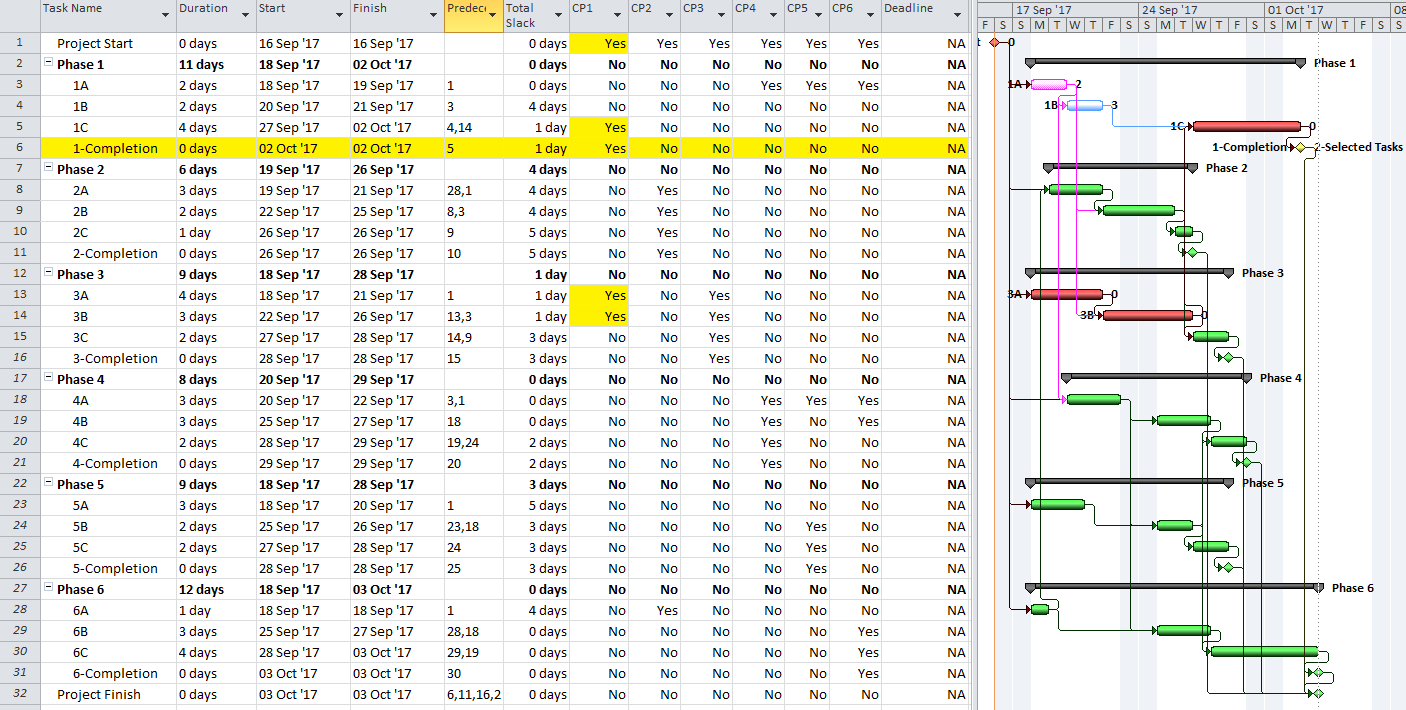
Here is a simple example project comprising six “phases” of inter-related tasks in a Microsoft Project (MSP) schedule.
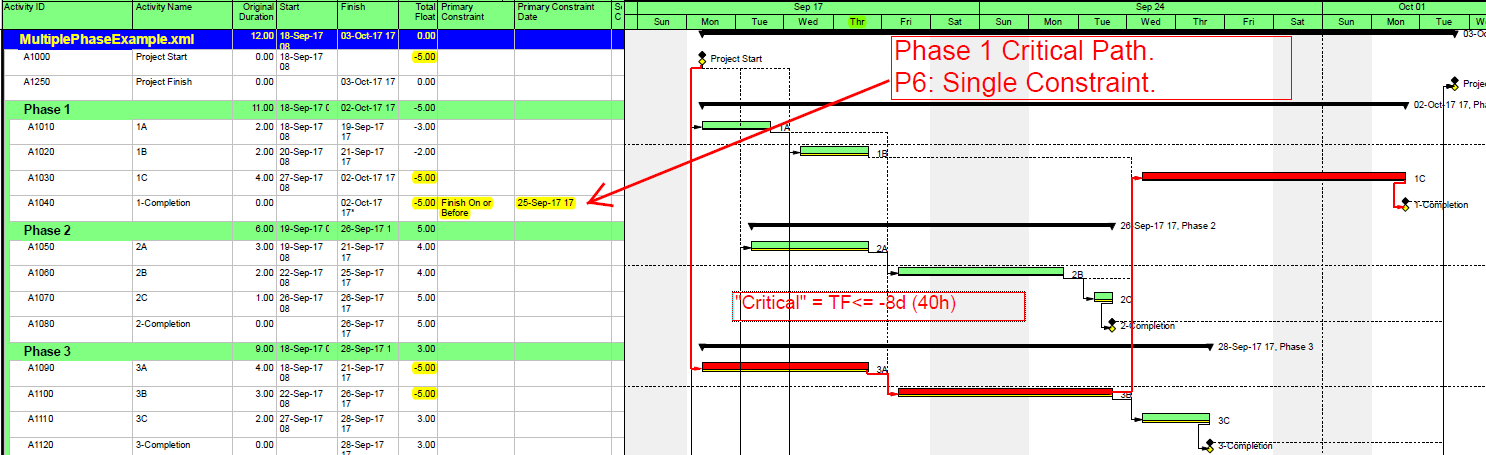
MSP identifies the CP for the project on the basis of Total Slack (TS<=0), and it colors the associated bars red. The table includes six columns identifying the critical/driving tasks for each of the phase-completion milestones (CP1 through CP6). For example, the critical/driving tasks for the Phase 1 Completion (ID #6) are flagged “yes” and highlighted yellow in the CP1 column. This path comprises the following sequence, which is easily verified by inspection: 1->13->14->5->6. Interestingly, the first Phase 1 task — ID #3 – “1A” — is marked “critical” for the overall project but is not critical for the Phase 1 Completion. A delay of this task would delay the project but would not immediately delay Phase 1. Coincidentally, since Phase 6 is the last phase to finish, its critical path (column CP6) corresponds to the critical path for the overall project – i.e. the red bars and TS=0.
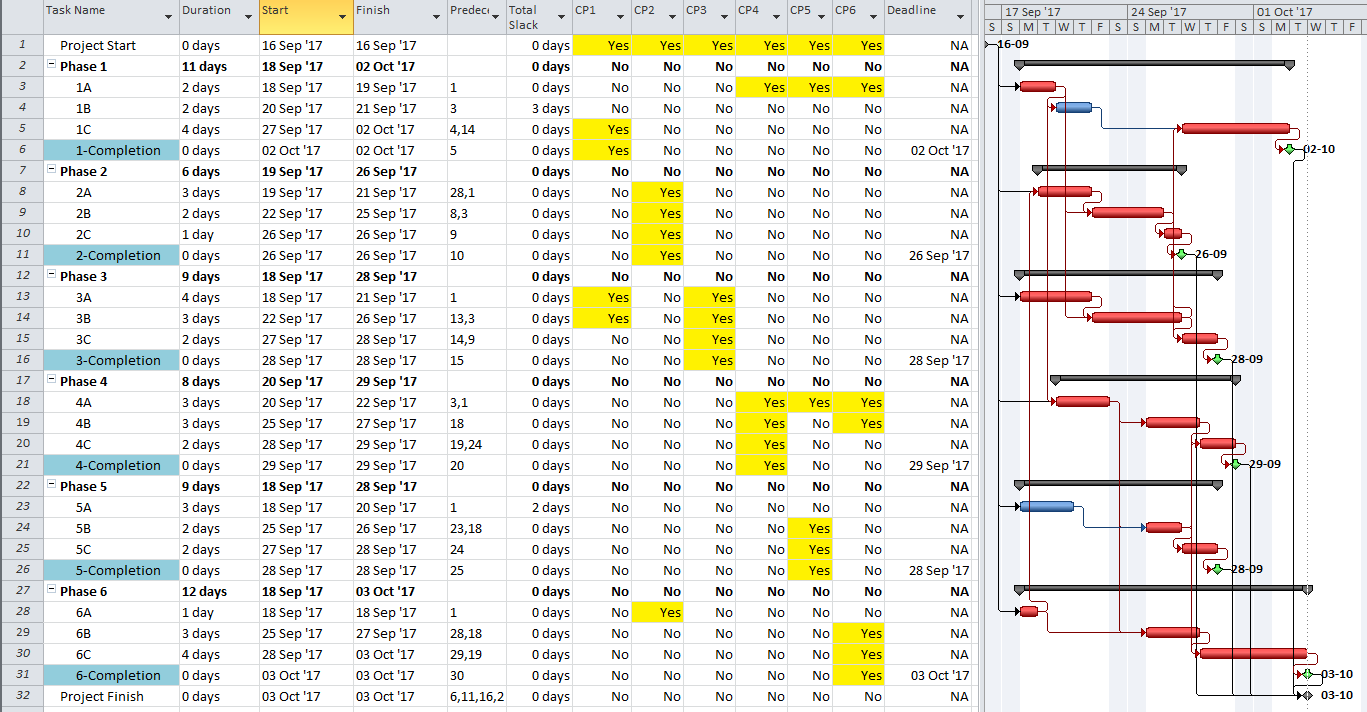
The project is scheduled identically using Oracle Primavera P6 (P6).
As a result of the modest number of inter-phase relationships, the critical/driving paths for five of the six phases include activities from other phases. The exception, Phase 3, is essentially self-contained, although several of its tasks are also driving the completion of Phase 1.
So, how are these six different critical paths identified?
Identifying Multiple Critical Paths
There is in fact no way to simultaneously define the critical paths to each of the six phase completion milestones of the example project using Total Slack alone without manipulation. The paths must be identified individually and directly reported (in the manner of BPC Logic Filter) or manually marked.
Deadlines / Late Constraints
It is common to apply deadlines (or late constraints in P6) to key completion milestones that are contractually defined – typically with financial consequences for delay. Deadlines have the potential to reduce Total Slack/Float, which MSP and P6 use to identify Critical tasks. When deadlines are applied to tasks and milestones that – together with their predecessor chains – are logically and organizationally separate, then Total Slack/Float can provide a reasonable indication of the driving path to each “deadlined” task or milestone. This is a rare circumstance. With only a single deadline applied, the Total Slack/Float for any task will be potentially influenced by the Project Completion date and by the deadline date, with the more “urgent” of the two forcing a lower Total Slack/Float value. With more deadlines and intersecting logic paths, the issue is multiplied.
In the present example, each phase completion task has been given a deadline corresponding to its current finish date. Consequently, all except two tasks in the entire project are given a Total Slack value of Zero and marked “Critical.” The delay of any of these tasks is certain to violate at least one of the deadlines, although the deadlines to be violated are not obvious without the table. The actual driving path to each phase completion remains obscured. Although not completely reliable for defining individual driving paths, deadlines (and late constraints in P6) remain useful for flagging those tasks whose delay could affect (or already have affected) a contractually significant milestone.
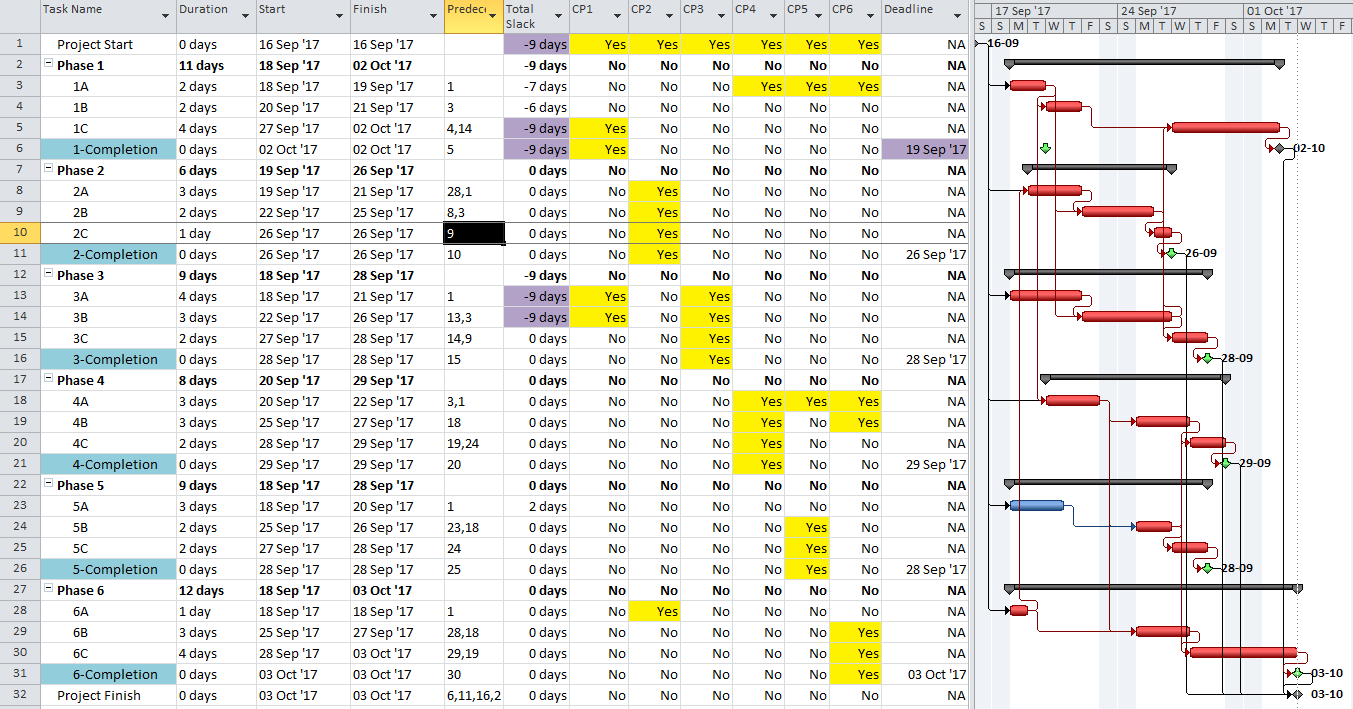
If the project already includes multiple deadlines (for contractually significant milestones), then the critical/driving path for each milestone can be identified (one at a time) by forcing the milestone onto the MOST critical path, i.e.:
- Temporarily accelerating the deadline date to the point that it becomes the most “urgent” deadline in the schedule network for all affected tasks. The Total Slack of the milestone and its driving predecessors is then easily distinguished from that of other tasks; and then
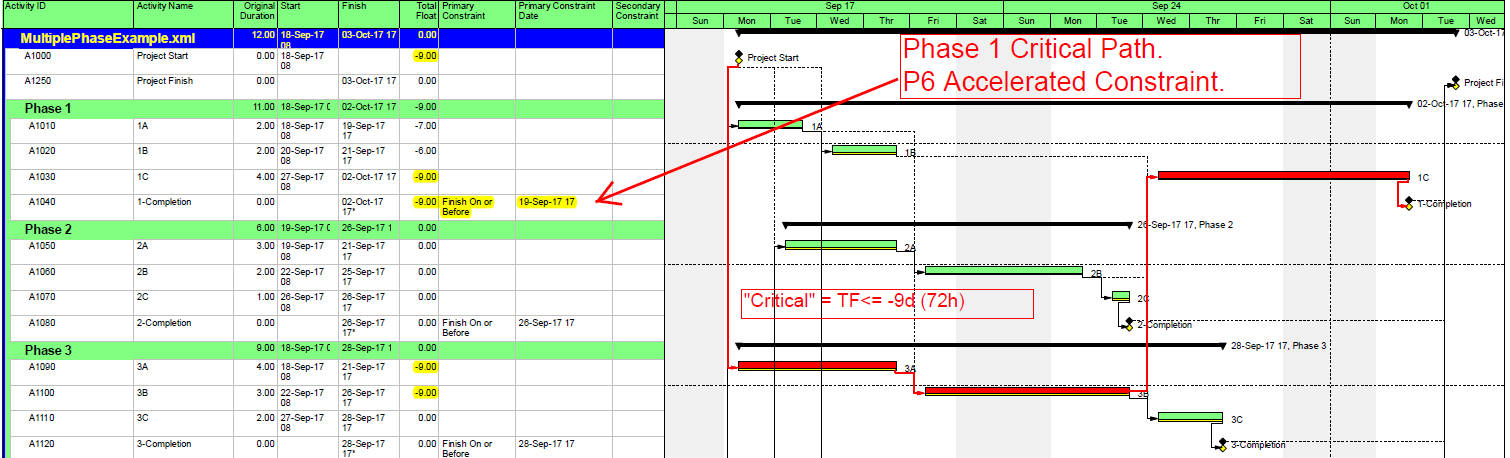
- Marking the tasks identified by the lowest Total Slack value. Here, the deadline for the Phase 1 completion was accelerated by 9 work days, resulting in a Total Slack of -9 days for the completion task and its driving predecessors. The CP1 custom flag field could then be marked accordingly.
As shown here, a nearly-identical process (using an accelerated Finish-on-or-before constraint) can be used for a P6 project schedule with multiple late constraints.
A similar approach can be used by adding a deadline or late constraint (in P6) if the project has none.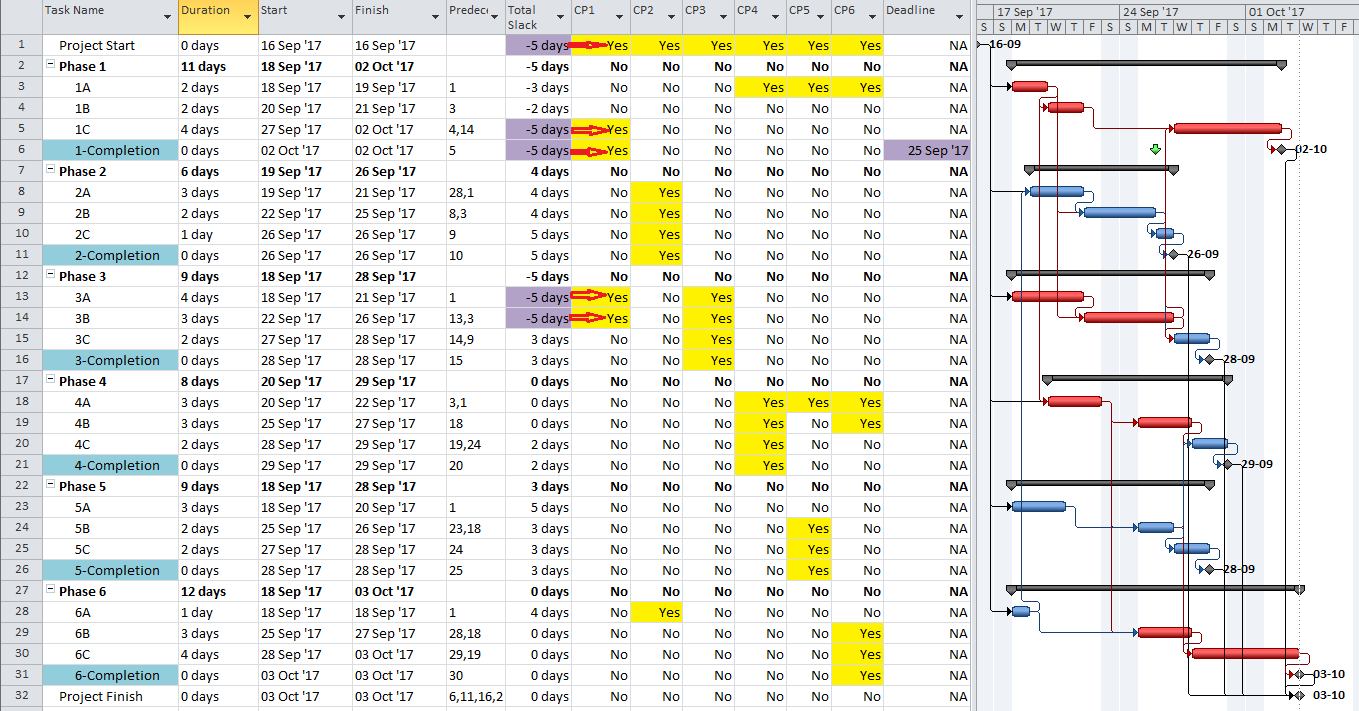
In fact this is the “Constraint Method” that was recognized by the Defense Contract Management Agency (DCMA) as the only valid method for defining a program critical path as part of its 14-point schedule assessment.
As shown above, using deadlines or constraints to generate negative slack/float is an effective way to identify multiple critical paths. In Microsoft Project, however, these paths are difficult to distinguish on the Gantt charts because their red bars are not uniquely differentiated from others. Both MSP and P6 can set the “Critical” flag – resulting in the red bars – for any tasks whose Total Slack/Float is below a certain user-specified threshold. Unlike P6, MSP does not permit this threshold to be less than zero. Consequently, all tasks with negative Total Slack – even those which are not driving anything – are flagged as “Critical” and given the red bar in MSP.
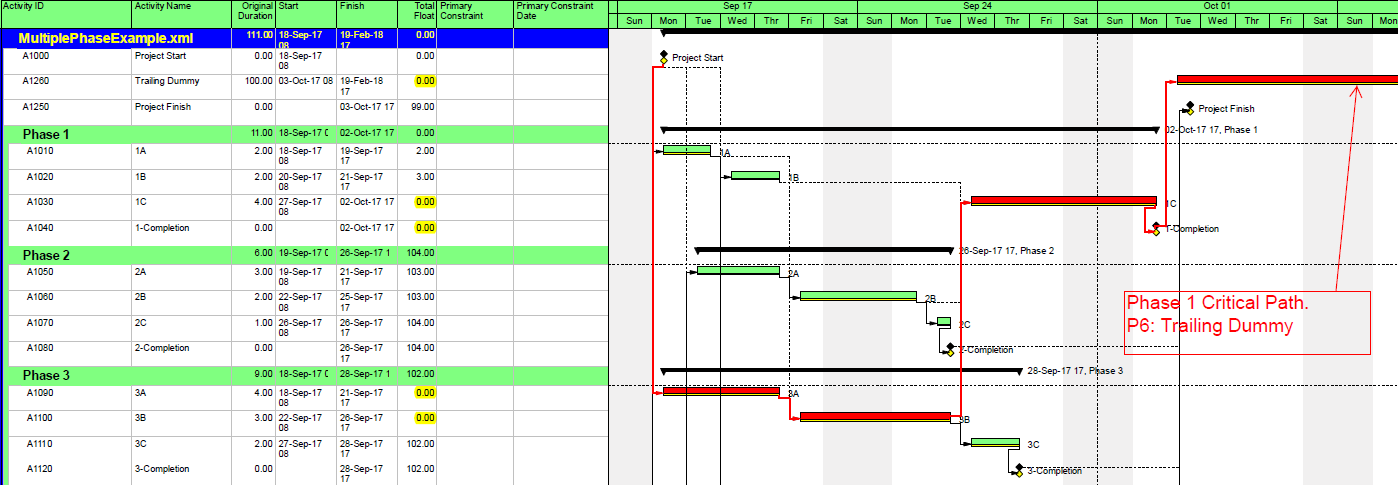
Trailing Dummy
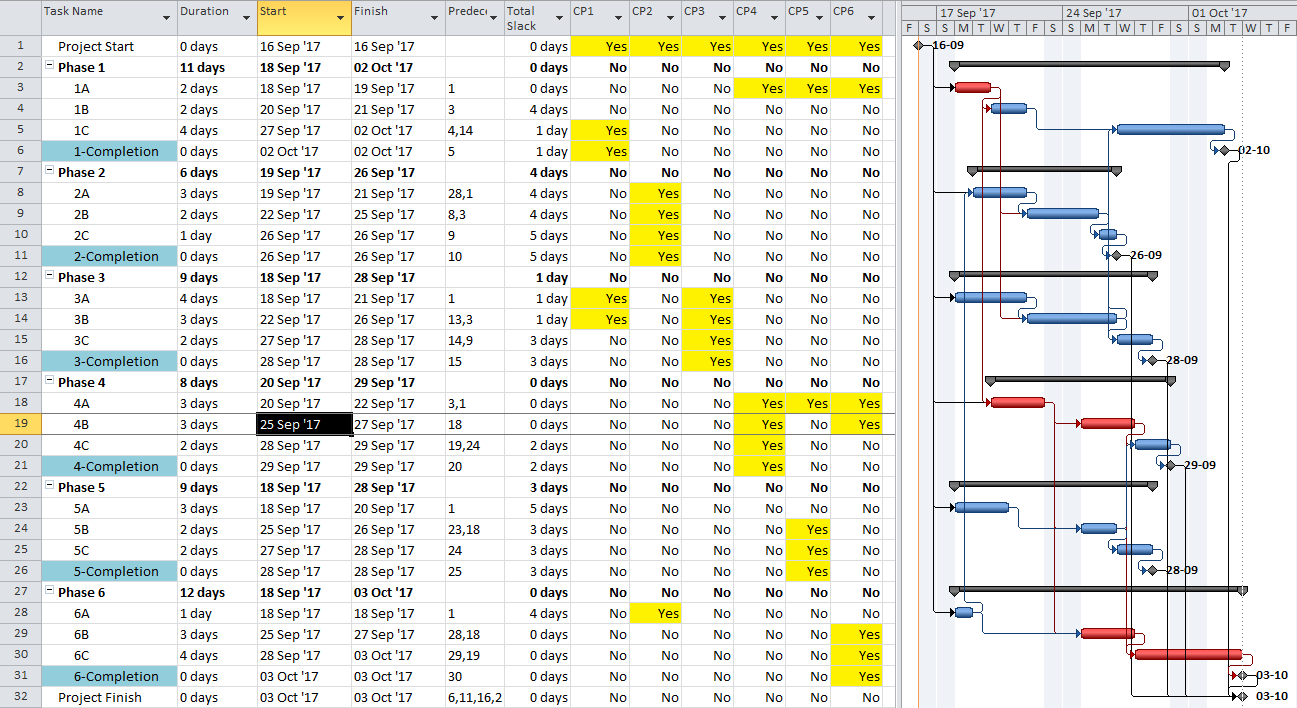
An alternate approach to overcome this limitation for presentation purposes uses a “super-long trailing dummy” task. In this approach, all deadlines and late constraints in the project must be removed (at least temporarily). Then a “trailing dummy” task is assigned as a successor to the first key completion milestone, forcing the milestone onto the critical path. The duration of the trailing dummy must be long enough to extend the completion of the project, creating positive Total Slack for all tasks that are not part of the dummy’s driving predecessor chain. As shown in the following two figures, adding the 100-day Trailing Dummy task as a successor to the Phase 1 completion milestone effectively creates a new critical path for the project – one which is easily recognized as the Phase 1 critical path on the Gantt chart. Moving the trailing dummy successor from phase to phase – one at a time – reveals the unique critical path for each phase. 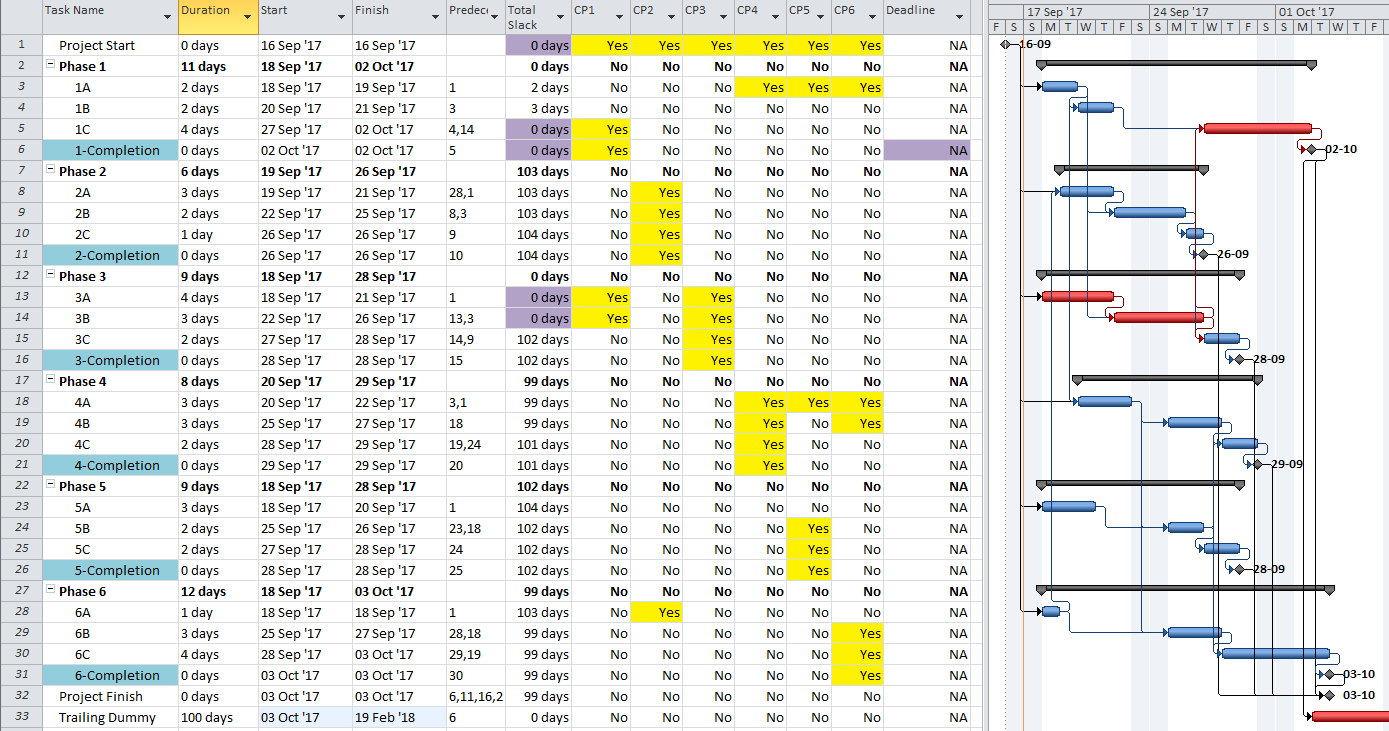
So far all of these approaches rely on temporary manipulation of Total Slack or Total Float, and it is important that such temporary changes be reversed prior to sharing or distributing schedule files. Obviously, these approaches can be labor-intensive and error-prone, making them impractical when the schedule status (and logic) is in flux – as during regular weekly/monthly updating. Even when the complications of multiple deadlines or late constraints are removed, Total Slack also becomes unreliable as an indicator of critical/driving relationships whenever multiple task/resource calendars or resource leveling are applied.
Driving Logic Tracing
The “Longest Path” algorithm in P6 defines the project’s Critical Path by automatically tracing driving logic backward from project completion. This avoids the complications that late constraints and multiple calendars introduce to the interpretation of Total Float, and it is the preferred calculation method when these factors exist. (It is unfortunate that P6 seems to be the only mainstream project scheduling tool to implement it.) Since the algorithm always begins the backward trace with the project completion activity, using it with the trailing dummy method above is useful for identifying multiple critical paths on the basis of driving logic. Driving logic can also be traced in other ways.
Driving Path Trace / Filter (P6)
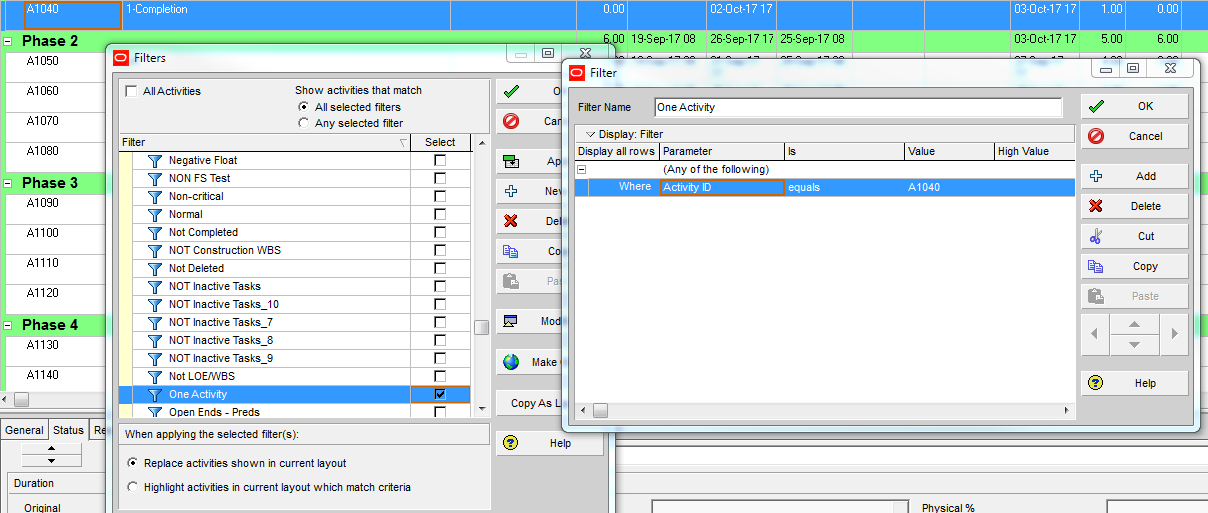
P6 automatically identifies driving and non-driving relationships in the task details. It also allows users to automatically add activities to existing filters by simply selecting them. The combination of these two features allows users to manually construct a filtered view of the critical path to any completion milestone by simply clicking backward through the driving relationships.
The first step is to construct a custom filter to isolate the completion milestone of interest. Here we are focusing on the Phase 1 completion milestone.
Next, the chain of driving activities (i.e. the driving path) is added to the view by stepping backward through the driving relationships using the “GoTo” button in the predecessors pane. Here is the view after taking the first backward step.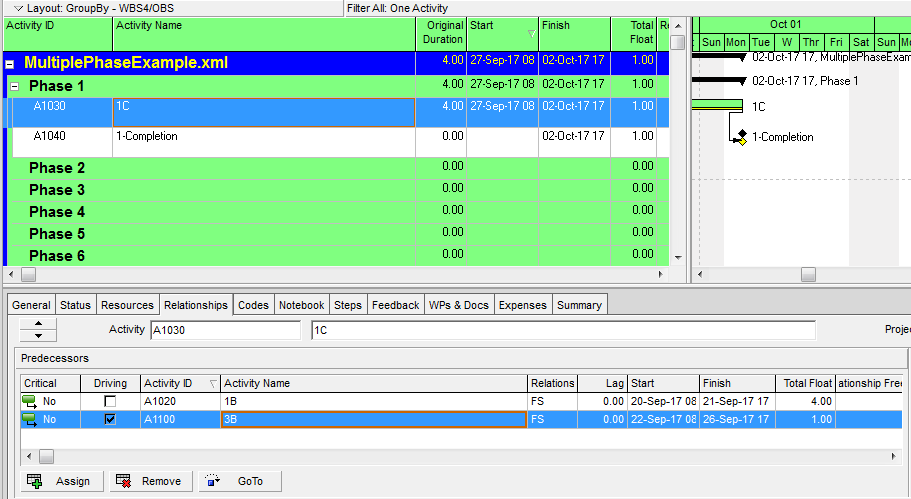
Here is the view after tracing the network all the way back to the first driving relationship. This is the driving (i.e. “critical”) path for the Phase 1 completion milestone. 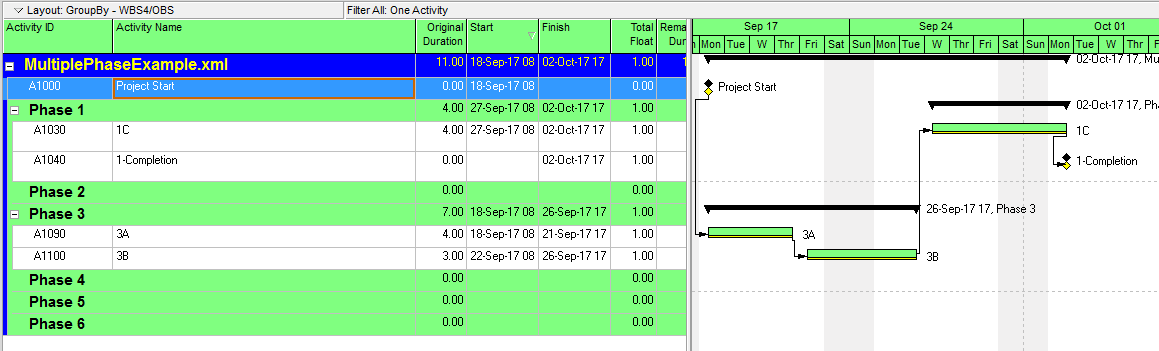
This click-tracing technique can become tedious when the project schedule is complex and there are numerous branches to the logic paths. For example, if an activity along the driving path has two driving predecessors, then the analyst must make a note to return to the second one after the first is fully explored. In addition, P6 routinely marks all links to Level-of-Effort (LOE) activities and links to ALAP-constrained predecessors as driving. The LOE activities must be ignored during the trace, and the ALAP constrained activities need to be evaluated separately. Finally, near-driving logic paths can be identified by the “relationship free float” field in the predecessors table, but isolating driving and near-driving paths involves creating and marking a number of new activity fields.
Fortunately, P6 includes an advanced scheduling option for calculating multiple float paths, which I’ve previously written about here. This option effectively automates the click-tracing technique.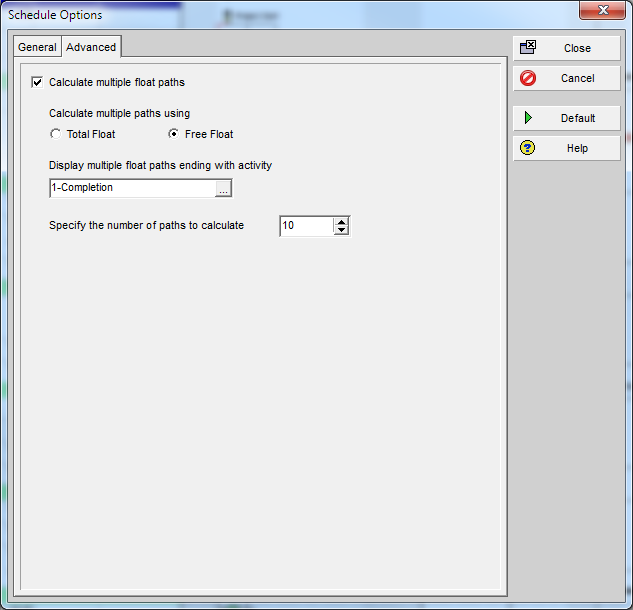
Combined with a view/layout/filter that depicts the “Float Path” field, this option provides a robust and repeatable method for defining the driving and near driving paths to each phase completion milestone in a P6 schedule. (The “free float” option must be used.) Float Path number 1 identifies the (first) driving path. Higher Float Path numbers identify any parallel driving paths and near-driving paths. Like the click-tracing technique, Multiple-Float Path analysis works without modifying the schedule network, so reversing temporary changes is not a concern prior to sharing the schedule. Neither of these techniques affects P6’s assignment of the “critical” flag, however, so red-bars on the Gantt charts are not meaningful.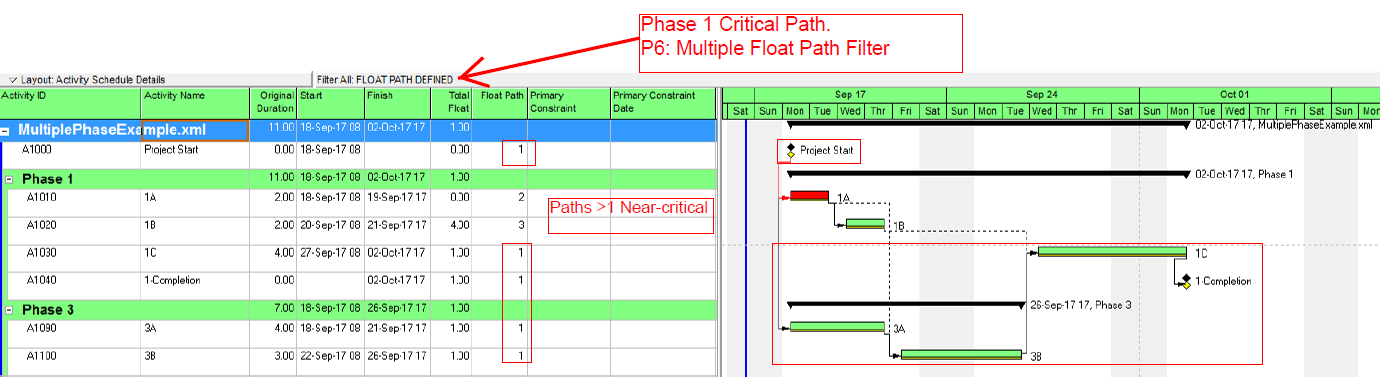
Task Path (MSP)
If you are using a recent version of Microsoft Project (2013+), then the driving path to each phase completion milestone can be visually identified and highlighted on the bar chart using the “Task Path” function with the “driving predecessors” switch selected. (Task ID6 is selected, and the tasks in its “Driving Predecessors” Task Path are highlighted orange.) The user can then manually enter a code (like the custom flag fields shown above) to mark the highlighted tasks. It is fairly straightforward to automate the generation of a task path filter using a macro, and some macro snippets have been published. (E.g. here.) Unfortunately, Task Path’s “Driving Predecessors” are not reliable for most complex projects (e.g. when non-Finish-to-Start links, in-progress tasks, or manually-scheduled tasks are present.) Those issues are discussed in my other blog entry here.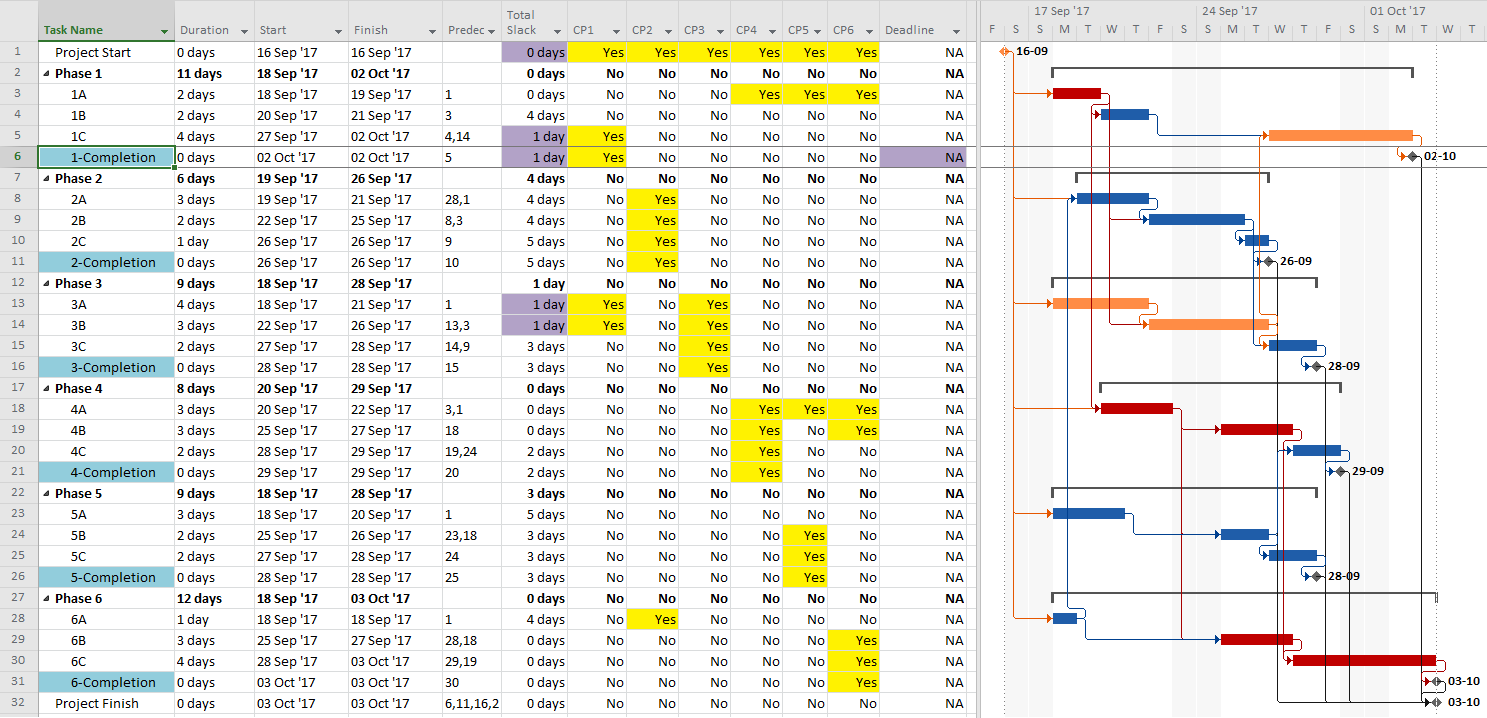
Logic-Tracing Add-ins
BPC Logic Filter (an MSP add-in) was developed in part to offset the absence of the Longest Path and multiple float path analysis in MSP. The chart below shows driving and near-driving paths to Phase 1 completion – depicted by altering the bar chart. The driving path is indicated by dark red bars with the zero indicating zero relative float. Consistent with the trailing-dummy results, the two non-driving tasks that are part of Phase 1 are depicted as having 2 days and 3 days, respectively, of float relative to the Phase 1 completion milestone. That is, they could slip 2 or 3 days before affecting the milestone. Similar depictions of the driving and near-driving paths for the other five phases, and for the project as a whole, are made possible with a few clicks. Since the schedule network is not manipulated in any way, Total Slack remains unchanged, and there is no need to reverse any analysis-based modifications prior to sharing the data file.
[See also Multiple Critical Paths – Revisited with BPC Logic Filter]
A Note About Open Ends
Some experts have suggested using open-ended logic along with a built-in software calculation setting to automatically mark multiple critical paths. The proposal is as follows:
- Ensure that each of the Phase completion milestones is sequenced so that a) it is a logical successor to all the activities in the phase, and b) it has no successors.
- Enable a calculation setting that forces activities with no successors to have zero total float. In P6, this setting is the “Make open-ended activities critical” schedule option. In MSP, the setting is the “Calculate multiple critical paths” advanced calculation option.
Effectively, this is the same as assigning a deadline to each completion milestone at a date that exactly equals its early finish date – an example of which was already explored above. It is subject to the same drawbacks of that approach, but with none of the advantages. I.e. If there are intersecting logic paths between phases (as shown in the example), then which activities are driving which milestone cannot be determined based on total float alone. One merely sees a bunch of zero-float activities in all the phases. Moreover, the basic technique of accelerating the milestone’s deadline/late-constraint date to reveal its driving predecessor path (through negative float) is not available when no deadline or late constraints have been applied. Between this and other failings, I just don’t see any advantages to this open-ends approach.
Recap
A project schedule can possess multiple critical paths for one of two primary reasons:
- There is a single key completion milestone at the end of the project, and multiple, concurrent, parallel driving paths to that milestone exist. In this case, the multiple critical paths often reflect a schedule model that is simpler than the actual execution of the project. Correctly accounting for productivity of the assigned resources may remove the apparent concurrency and restore the single Critical Path, but the increased overhead of developing and managing a more detailed schedule would need to be justified.
- The project possesses multiple key completion milestones, each with its own legitimate driving/critical path. In this case, the correct identification and status reporting for the multiple Critical Paths is often beyond the capabilities of the scheduling software. Then specialized logic tracing techniques are required.
These factors can also be combined in some project schedules.
Excellent article, Tom. I always enjoy your thoughtful writings. I have long argued that the conventional idea that there is but one “longest” or “least float” critical path for every Schedule was over-simplistic. I devoted substantial to this in both of my books. Kudos for clarifying a greatly misunderstood point.
Thanks, Murray. Having read (parts of) your book, Faster Construction Projects with CPM Scheduling, I’ve found a lot we agree on.
Tom,
In my second book, “CPM Mechanics,” I spent an entire chapter on a concept developed by ICS-Research, called Multi-Path Analysis and Paramount Paths. The concept achieves two needed innovations. First, as you discussed, it recognizes that, for each mandatory deadline imposed on a CPM schedule, there are one or more driving paths.
Second, though, the concept criticizes Total Float (or, Slack, in MSP parlance) as a comparative value, thus an unstable one. In a given example, the teacher might think of Johnny as the “sickest” because he has a cold. But then Mollie comes in with measles and she is now the “sickest.” When Mark comes in a with a broken arm, he is now the “sickest.” More significantly, Johnny is no longer a concern for the teacher, because is no longer the “sickest.”
From a managerial perspective, the conventional wisdom, as advocated by Dominant Project Management, is that the Project Team (and PM, in particular) should focus their greatest attention on the “most critical” activities. As they abide, and as “criticality” flips around, liked a downed power line, the Project Team jumps from one “critical” path to the next. Hence, the instability.
To correct this exhausting, counter-productive, and often project-delaying management reaction, ICS-Research conceived of a set of quantitative measures and corresponding terms. Think of how storms are rated (by Miles per Hour) as Tropical Depressions, Tropical Storm, and then Hurricanes. And even hurricanes are further categorized by wind strength into different “Categories.”
Likewise, in healthcare, there are rigid definitions of stable, critical, intensive care, acute, terminal, etc. One does not STOP being terminal because someone else, also terminal, has a shorter period of time left on earth.
And so, ICS-Research developed a “ranking system” based on percent of remaining path length compared to Float/Slack status. For instance, if there are 50 weeks left to Project Complete, and the Least Float has negative 5 days, then that would constitute a 10% overrun, right?
Now, if we have a table that associates a label (e.g., “Urgent”) to the percent range from 6-10%, then this path would be labeled Urgent.
Finally, as you and I both know, virtually every imposed deadline has more than one path feeding into it. Using the Path Ranking System, one can label each path. Informed by this, we can now establish FOUR new pieces of information about that Deadline, One, the number of paths feeding into it. Two, the Ranking of each path. Three, the Average of the Path Rankings. The Rank and Identity of the most driving path, which we call the Paramount Path.
It should be obvious that, by developing this information for each Imposed Deadline, we can create a comparative view of ALL Deadlines, and know which one(s) to focus our attention on.
If you wish more information about Multi-Path Analysis and Paramount Paths, check out this ICS-White Paper. http://continuingscheducation.com/ics-continuing-scheducation-library/ics_white_papers/ics-white-paper-schedule-acceleration-free-float-multi-path-analysis/.
Hi Murray. Thanks for this further exposition. I haven’t read the paper, but the abstract reminds me of what Tal Levanon has been doing at HCP Consulting in Israel. The HCP (Hidden Critical Path) method seems to involve exhaustive examination and classification/ranking of every single logic path in a project schedule. Tal has presented the method a few times at the Construction CPM Conference. Unfortunately, between Risk consultants deriding the value of deterministic schedules and AI-driven scheduling tools now coming into play, the project manager who understands (or even appreciates) logic paths and their consequences seems to be an endangered species. Rgds, tmb
Tom,
I am aware of Tal’s good work. However, my impression is that the greater contribution of his work, as his anecdotal white paper narrates, is simply to explain the value of developing a sufficiently comprehensive CPM schedule.
As to the further clarificaton of his “hidden critical paths,” I have a few causes of heartburn. First, on a semantic level, I think his use of the word “critical” as he explains it. Nowhere in his explanatory documents have I found a clear rule for determining when a secondary path is “critical” or “near-critical.”
Second, I cannot help but feel that the very concept of a “hidden” path is little more than a marketing ploy. After all, CPM has included Total Float values since its inception over 50 years ago. The point of Total Float is to numerically represent the path duration gap.
In our studies at ICS-Research, we long-ago moved beyond the obvious (awareness that some paths are longer than others) into identifying the activities that reside on the most paths at the same time. Such identification allows for targeted concentrations of effort where we can get the “biggest bang for the buck.”
Further, our work on Multi-Path Analysis logically led to solving the problem with the conventional definition of what ‘s “critical,” which is that the term is comparative, as I wrote to you about earlier.
Tal’s approach continues to ignore the ambiguity and distortions of a path moving from “Critical” to “Near Critical,” simply because some other passes suddenly becomes longer.
But his Hidden Critical Path Method actually exacerbates the problem because, thanks to his lax use of the term “critical,” under this definition, even more activities become “critical.”
To illustrate my point, revisit his sample Report on his website, where he notes that out of 166 activities, 63 are “critical.” That amounts to 38% of the activities in the schedule being “critical.”
I don’t know about you, Tom, but if I had a schedule where 38% of the activities were “critical” I sure wouldn’t be expertly opining that “this indicates a minimally risky project.”
There is an old expression along the lines of, “if you have 10 things to do, and all 10 are Priority #1, the YOU HAVE NO PRIORITIES.” This method reminds me of that adage.
I do not disagree that the typical CPM schedule is comprised of a spaghetti-bowl of interwoven sequences of activities. But rather than simply measuring the differences in their lengths relative to one another (think: Free Float), why not vector in on activities that have the greatest influence on the most paths?
You may want to look into our work on Activity Path Resiliency and Activity Path Vulnerability. ICS-Research has developed algorithm that dare to speculate on the likelihood that an activity might slip (vulnerability), as well as the potential for an activity to eliminate, or make up for, incurred delay (resiliency).
By aggregating the two values (per activity) to all the activities on any given path, and then by further associating these Path Values to all of the paths that feed into a given Milestone, we can arrive at both Vulnerability and Resiliency values for each milestone.
Take a moment to digest this. With this information, Management can quickly rank the milestones in terms of their potential for slippage, and just as easily recognize those activities that should be blitzed to achieve whatever recovery can be had for those milestones.
There is much good work to be done in this area. We are always looking for Early Adopters to provide test projects for our studies. We have had remarkable success on real projects, but always welcome more.
Dear Murray,
Thank you for your attention to my work and for reading my ‘white paper’ on the http://www.hcp-consulting.com website.
I would like to add some brief info to this interesting exchange of opinions and perhaps raise a suggestion.
The patented HCP method is based on mapping the paths in the network – and calculating each path’s duration. The HCP duration-slack is per path – comparing each path to the longest path in the network. The CPM, as you know, calculates the slacks per each task (total slack, free slack etc.), comparing every task to its successors and predecessors.
Thus, the different terminology: The HCP critical path(s) is the longest path(s), while any shorter path is a hidden critical path.
Quick note: the HCP and the CPM are not excluding each other. On the contrary – they complement one another. In real life, the HCP and the CPM bring the same results in rare cases only.
How many paths can be found in a network? (Spoiler – it can reach into the millions, I’ve seen it!). What can be done when there are too many (how many is “too many”?), how does the software “decide” what is the threshold for hidden critical paths and much more – these are all issues for another discussion.
The HCP analysis report includes also:
(1) Project Success Expectation based on the HCP score and some other parameters.
(2) Schedule Integrity Analysis – this topic includes six issues. Some are not so trivial and point out things that can happen in schedules on paper but cannot happen in real life.
(3) The HCP Critical Path Analysis comes with unique features as the HCP Paths Histogram. This histogram can tell you in a glimpse – what is the structure of the project schedule – and you can easily figure out the meaning of that…
Murray, you make an interesting point about our use of the word “critical”; it might have been better to choose other language. That said, I’d encourage you use our free app on one of your schedules, which you can find at http://analysis.hcp-consulting.com/HCP/
I think you might find our utility as helpful – that certainly has been the experience of the many contractors, project managers and high management executives on more than 200 projects that have used HCP in their construction of stadiums, bridges, tunnels, skyscrapers, infrastructure projects, high-tech projects, mega projects etc.
Besides that, I would like to invite you to Israel, to visit the holy land so we can meet in our office and have a great professional discussion! As I see it, we aren’t competing – but completing – and this common focus can only aid our profession!
Best regards,
Tal.