Primavera P6/P3/ST – Page 2

How to Find Multiple Critical Paths in a Single CPM Schedule

In complex project schedules, multiple critical paths can exist between the project’s start and finish milestones. Additionally, integrated projects with multiple phased scopes of delivery often have several distinct, contractually-mandated deliverables and corresponding delivery dates. Each possesses its own critical/driving path.

[Note to searchers: This article has a slight mention of Microsoft Project’s Advanced Calculation Option – “Calculate Multiple Critical Paths.” It’s near the end, in the section called A Note About Open Ends.]

A key tenet of the original Critical Path Method (CPM) of project scheduling is that each project has one and only one “Critical Path” (CP) that extends continuously from the project start milestone to the project finish milestone. The CP is defined by the collection of activities that determine the finish date of the project, such that a delay of any one of them will delay the project. Traditional methods identify the CP based on Total Slack/Float. For an elementary review, have a look at The Ultimate Guide to the Critical Path Method over at projectmanager.com.

[As demonstrated in this heavier article of mine, the CP is in many cases not actually defined by the collection of “Critical” activities from the software.]

Single Finish Milestone w/ Parallel Drivers

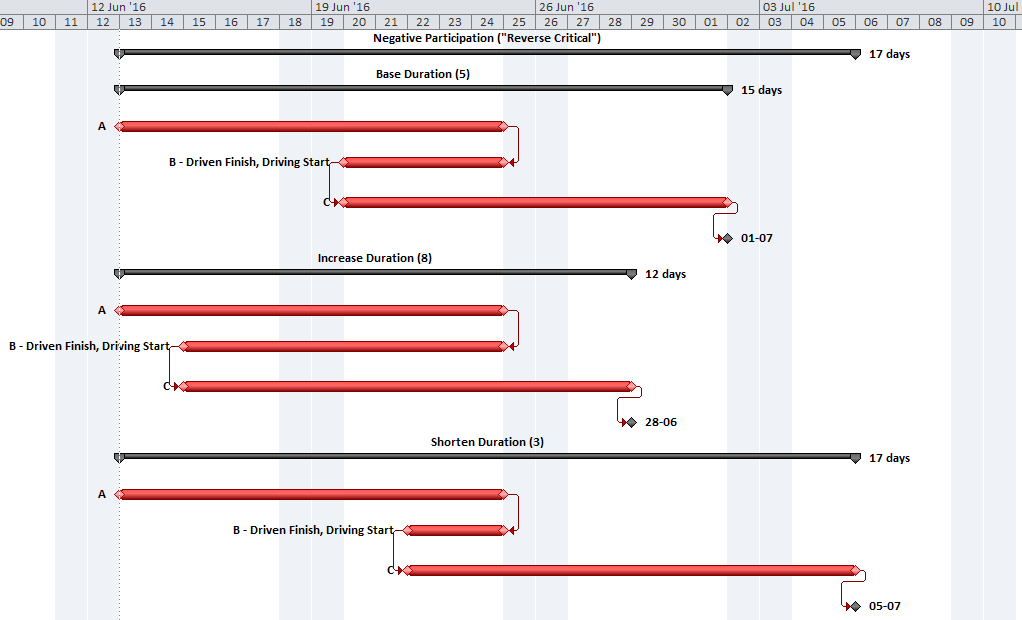
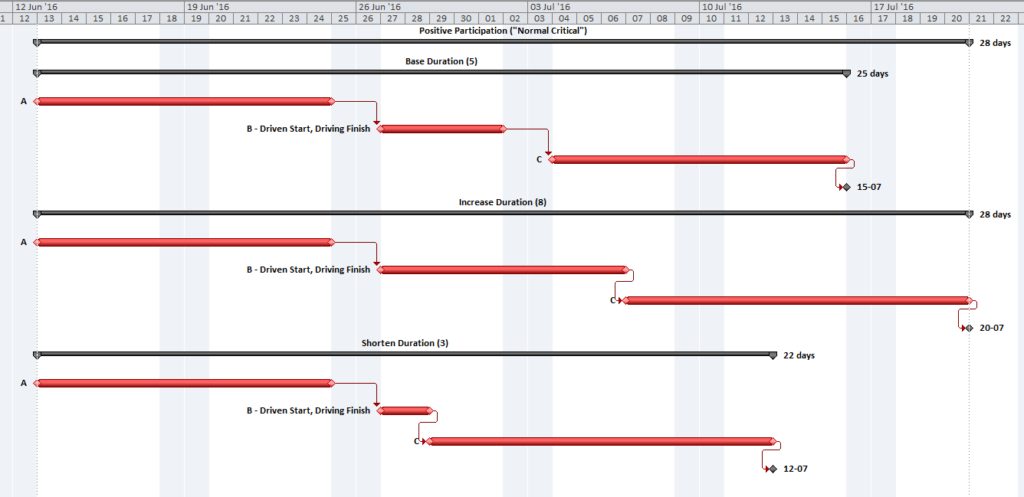
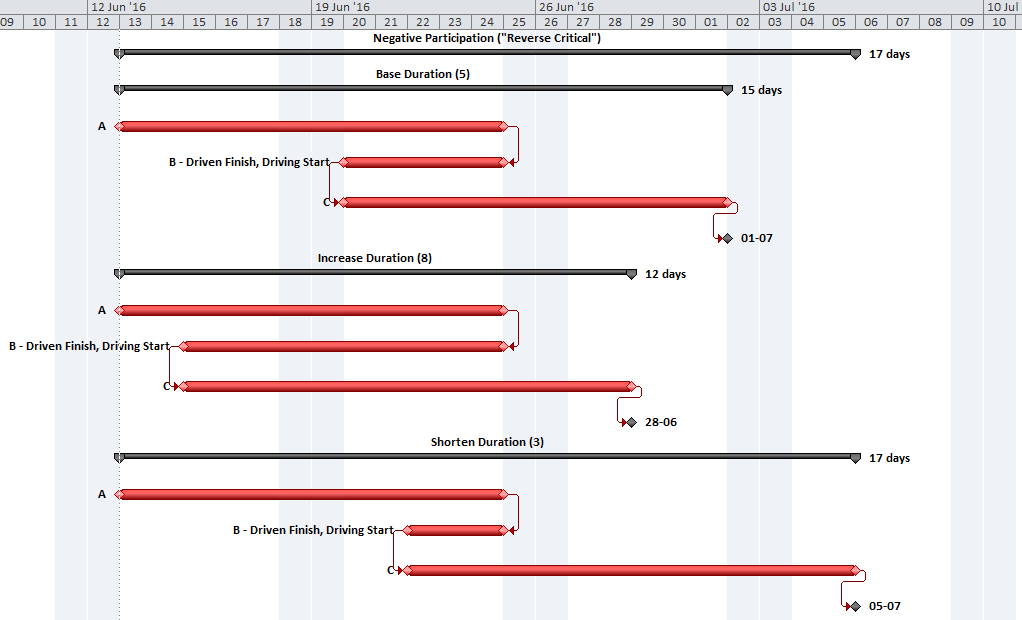
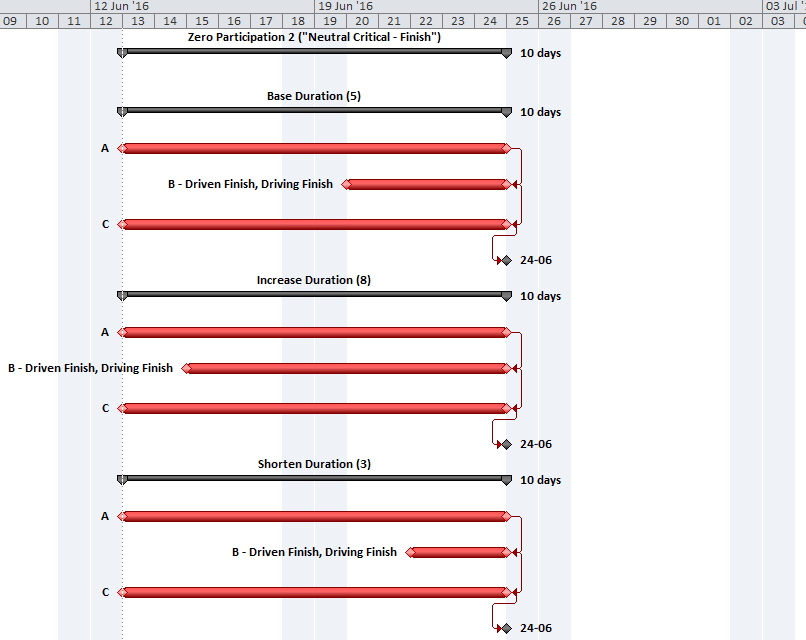
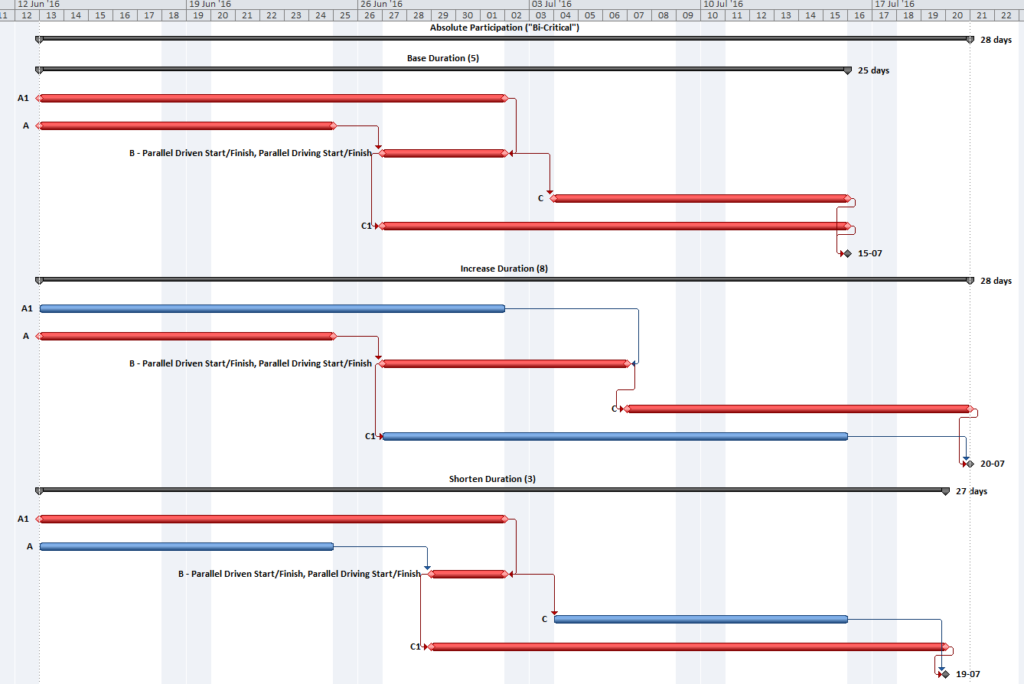
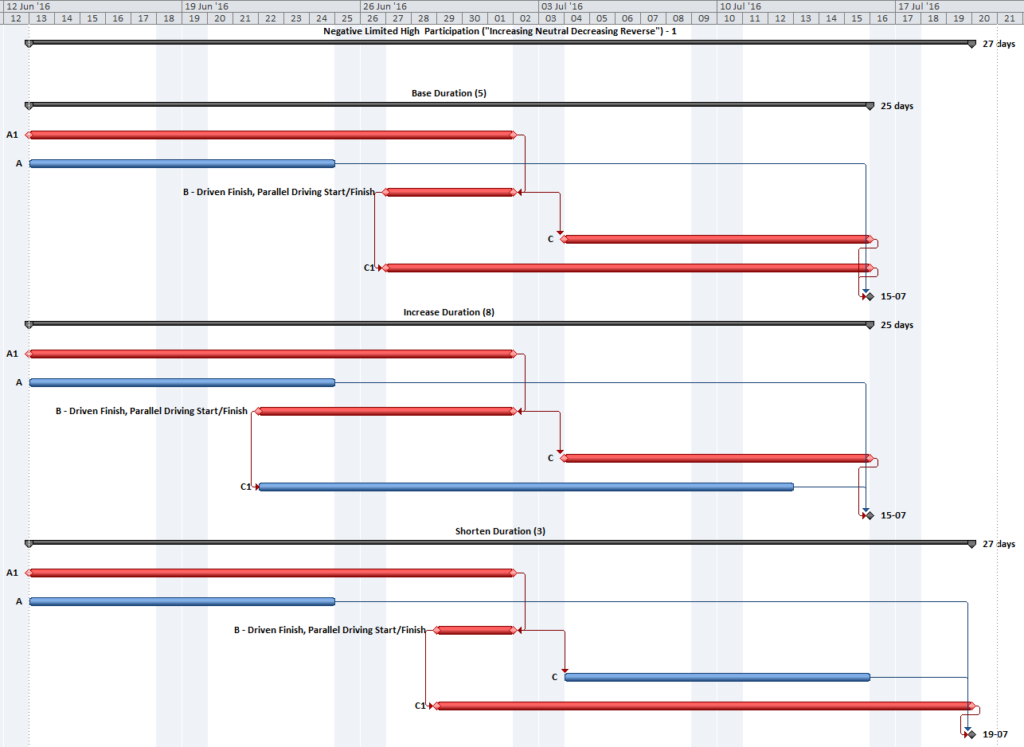
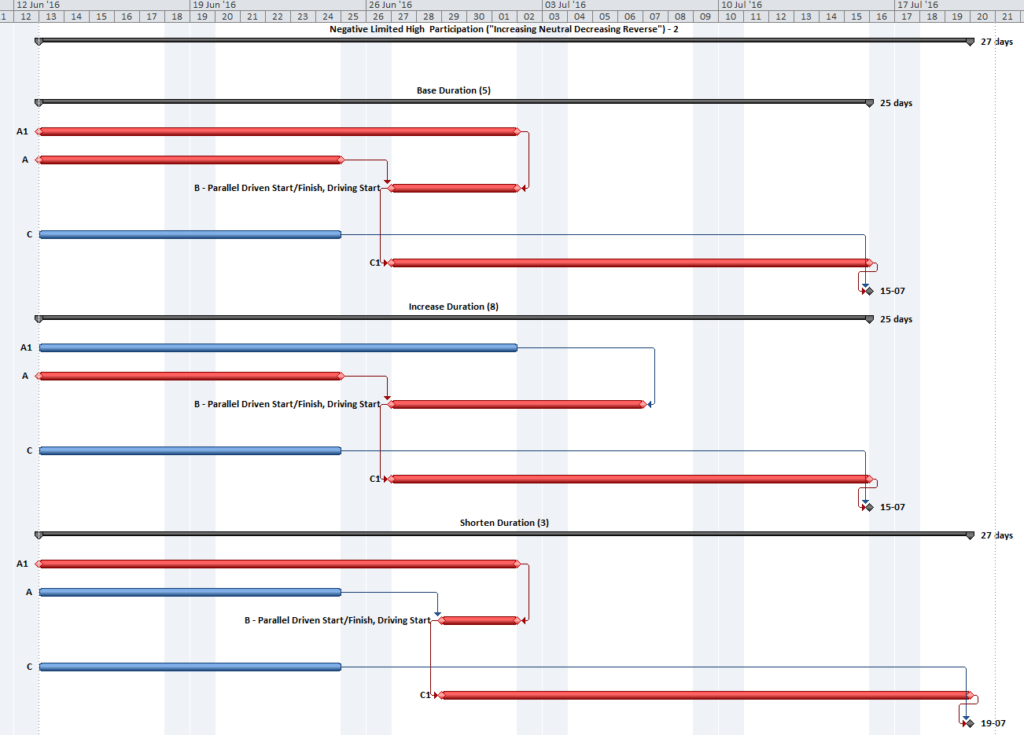
It is possible for the “critical path” between the start milestone and the finish milestone to have several parallel branches of equivalent length. These can be described as “multiple critical paths.”

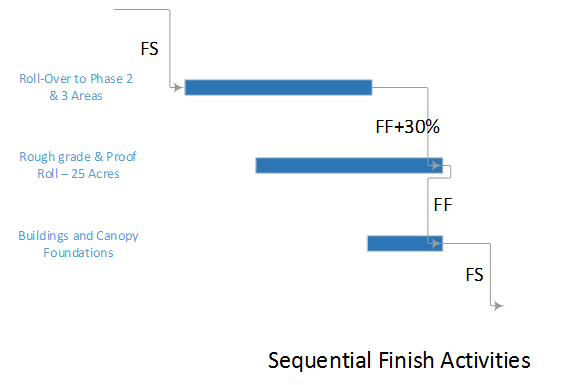
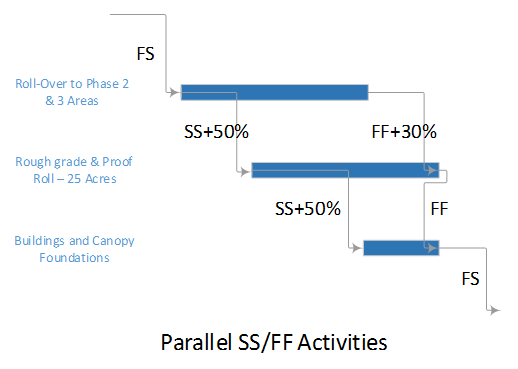
Depending on the details of the schedule model, it is not uncommon to have at least a few activities that are both concurrent and critical. That is, they comprise parallel branches of a common logic path that drives the completion of the project. For example, the construction schedule for a residential building may include one activity for “plumbing rough-ins” and another activity for “electrical rough-ins” (where “rough-in” is another term for “first fix” work.) The two activities have the same driving predecessors (e.g. structural framing) and driven successors (e.g. wall finishes), and they take the same amount of time to complete. If the wall finishes are on the driving path to project completion, then the two rough-in activities form parallel branches of the “Critical Path” for the project. Such parallel branches might be repeated for each floor of a multi-story building. In practice, instances of parallelism/concurrency that comprise only a few activities like those described here seem rarely, if ever, to be identified as “multiple critical paths.” This is because a) the parallel activities are seen as closely related; and b)traditional methods of identifying and depicting critical activities do not differentiate between the associated logic paths, typically sorting by dates and filtering primarily on the software’s “critical” flag and/or Total Slack/Float.

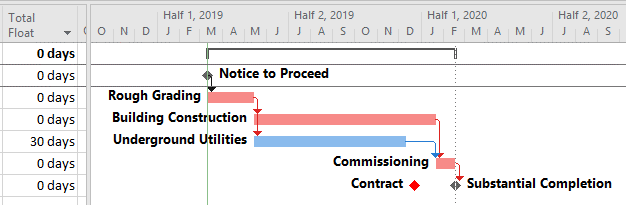
Multiple critical paths are also created by efforts to accelerate the project completion, such as crashing or fast-tracking exercises, after the initial development of the schedule. For example, a large scale construction project must be accelerated by 40 days to meet contract commitments. The critical path of the initial project schedule runs through building construction, while underground utility development activities possess 30 days of Total Float.

Additional resources (and costs) may be applied to compress the building construction activities by 30 days and yield a corresponding acceleration of the project completion. At that point, the building construction and utility development activities must both be compressed by an additional 10 days (and at additional cost) to obtain the necessary 40-day acceleration of the project. After the exercise, the building construction and utility development activities are equally driving the project completion, and the schedule possesses two critical paths.

Further crashing or fast-tracking exercises may add more critical paths. The associated activities all possess the same total float/slack, and all are marked as “critical.” Differentiating between the various paths requires a method for separately tracing and coding driving logic, either analytically or by visual inspection. Such methods are explored later in this article.

In practice, multiple critical paths are also created during project execution, as float is completely consumed by unplanned delays in activities that were previously non-critical. Exploration of such delays will have to wait for another article. (Notions of the “Critical Path” are sometimes suspended in the late stages of major/mega projects, as virtually every incomplete activity may delay the ultimate completion of the project and is therefore “Critical”.)

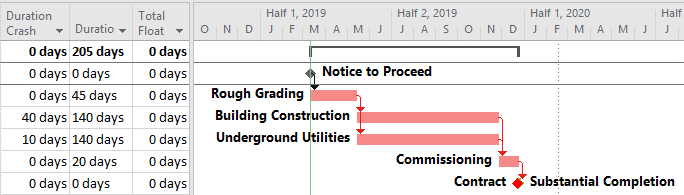
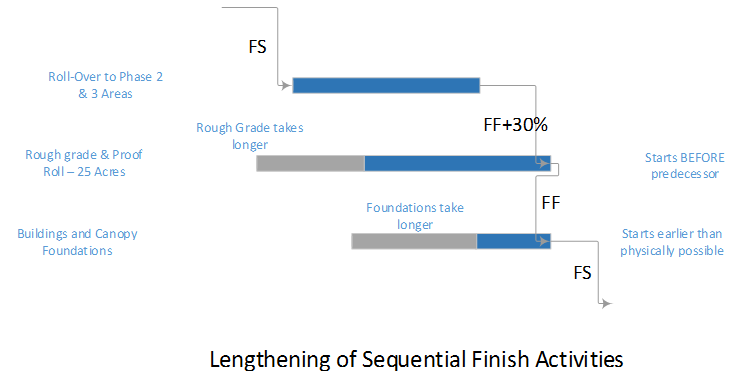
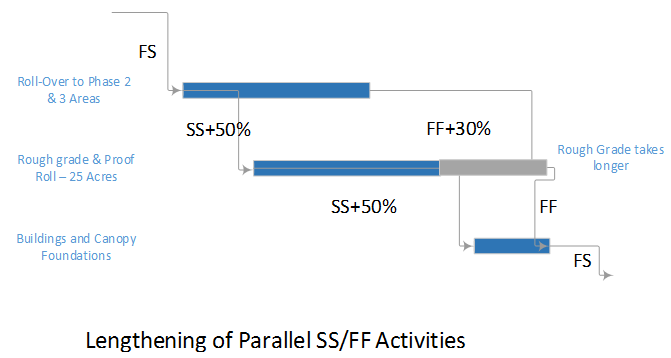
Ultimately, all three of these instances of multiple critical paths can be traced to a certain simplification (or presumed simplification) of resource utilization in the project. In the first example, plumbing and electrical crews are presumed to have exactly the same productivity, resulting in the same duration for both activities. In fact, one of the crews may be capable of completing the work sooner but paces its effort in order to match the scheduled duration. In the second example, it is presumed that the building construction activities and utility development activities may be compressed by exactly 40 days and 10 days, respectively. In fact, optimum resource usage often follows a step-wise rather than linear (or even continuous) function; consistent with adding discrete crews or substituting higher-capacity equipment. Thus, the building construction may be optimally compressed by 35 days or 45 days (not 40 days), and the utility development may be optimally compressed by 9 days or 12 days (not 10 days). As a result, the project completion is optimally accelerated by 42 days (not 40 days), with the critical path being governed by utility development. The crashed building construction activities get 3 days of float.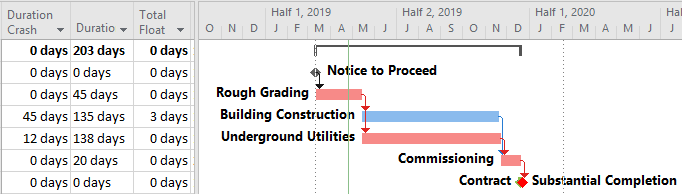

When taken to this level of detail, a single critical path may indeed be re-established. Depending on the needs of the project, such detail may or may not be justified in light of various project uncertainties and the increased management effort involved.

Multiple Delivery Milestones

When a project involves the parallel or interim delivery of multiple scopes of work, each delivery may be construed to have its own “critical path” – i.e. the sequence of activities and relationships determining the delivery date for the particular scope of work. More importantly, any particular activity in the project schedule may be expected to participate in more than one of these multiple critical paths. Examples include design, setup, or testing activities that may be common to several deliveries.

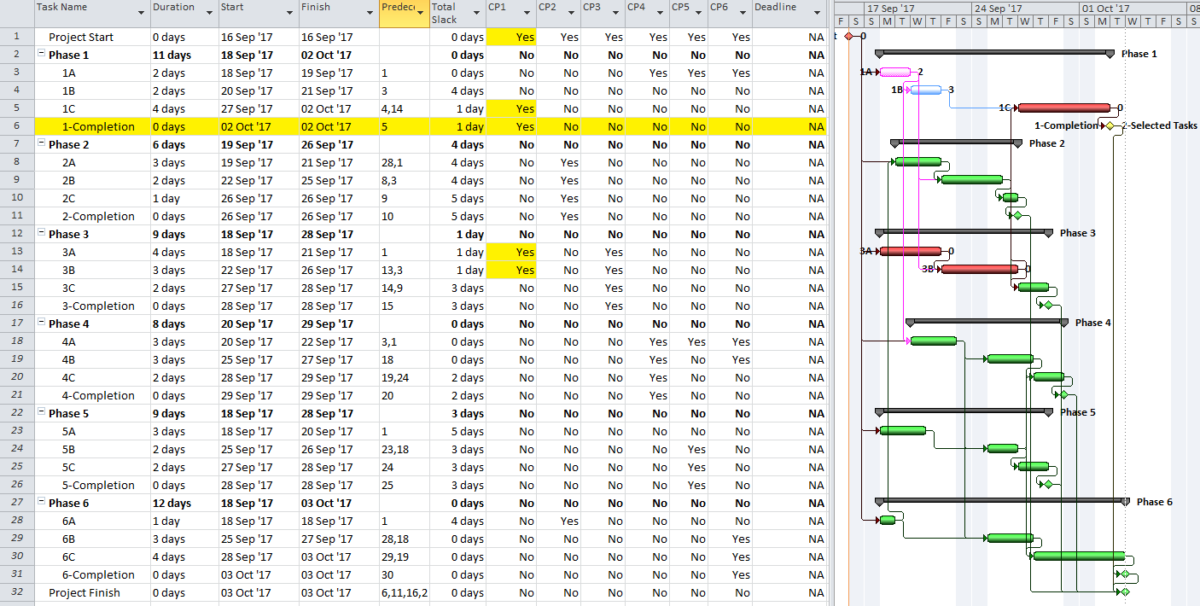
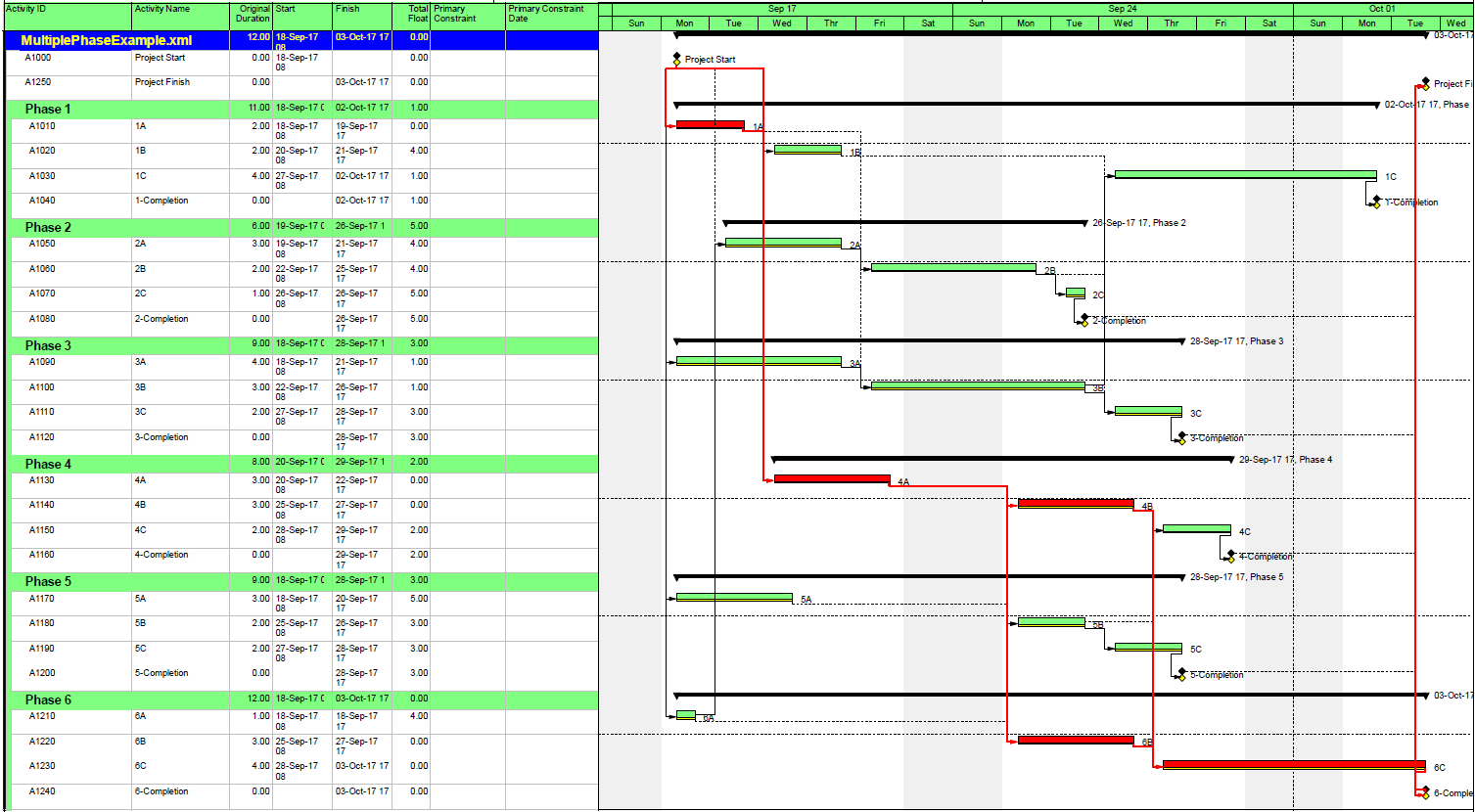
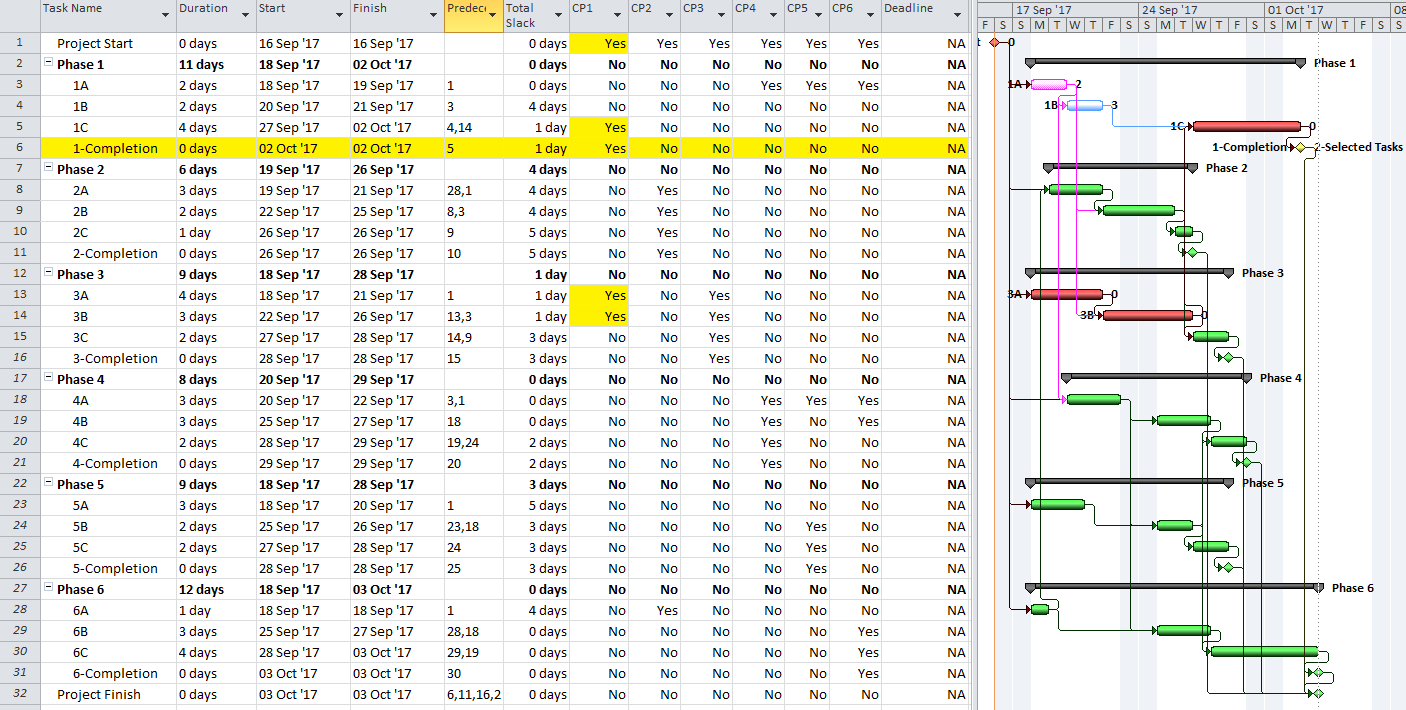
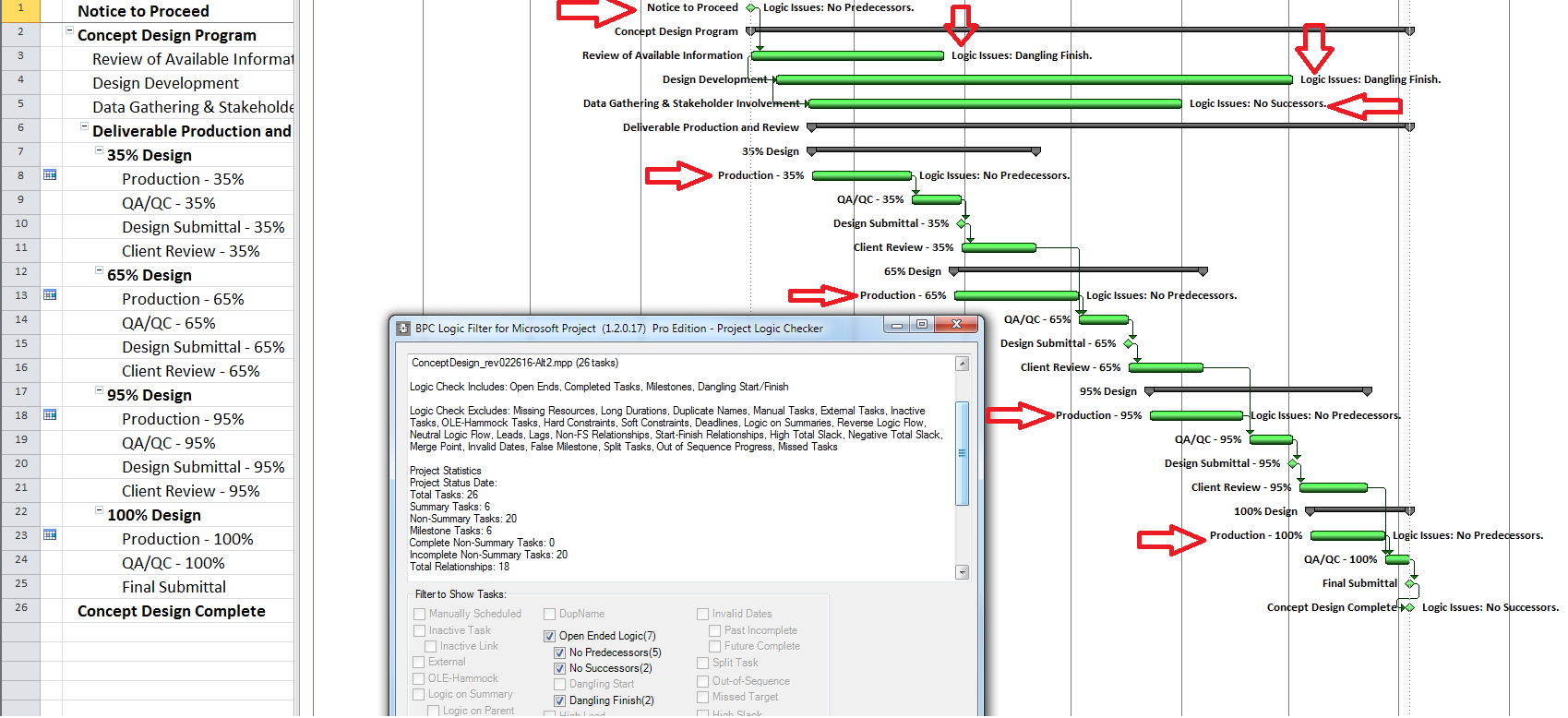
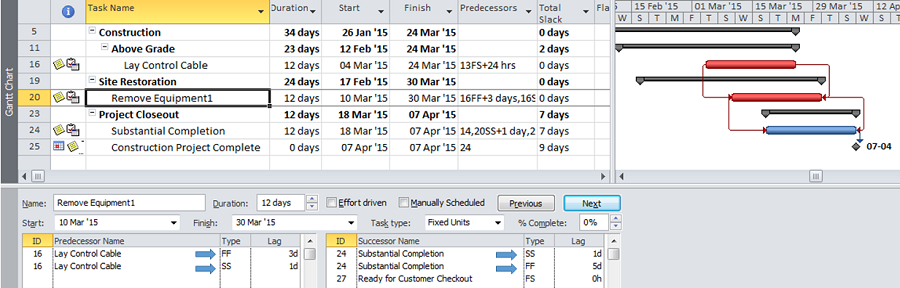
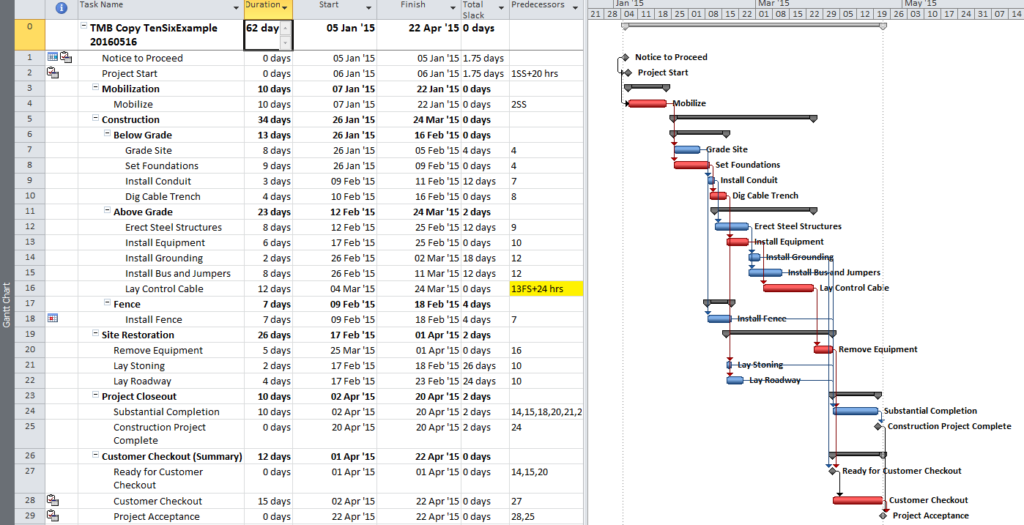
Here is a simple example project comprising six “phases” of inter-related tasks in a Microsoft Project (MSP) schedule.

MSP identifies the CP for the project on the basis of Total Slack (TS<=0), and it colors the associated bars red. The table includes six columns identifying the critical/driving tasks for each of the phase-completion milestones (CP1 through CP6). For example, the critical/driving tasks for the Phase 1 Completion (ID #6) are flagged “yes” and highlighted yellow in the CP1 column. This path comprises the following sequence, which is easily verified by inspection: 1->13->14->5->6. Interestingly, the first Phase 1 task — ID #3 – “1A” — is marked “critical” for the overall project but is not critical for the Phase 1 Completion. A delay of this task would delay the project but would not immediately delay Phase 1. Coincidentally, since Phase 6 is the last phase to finish, its critical path (column CP6) corresponds to the critical path for the overall project – i.e. the red bars and TS=0.

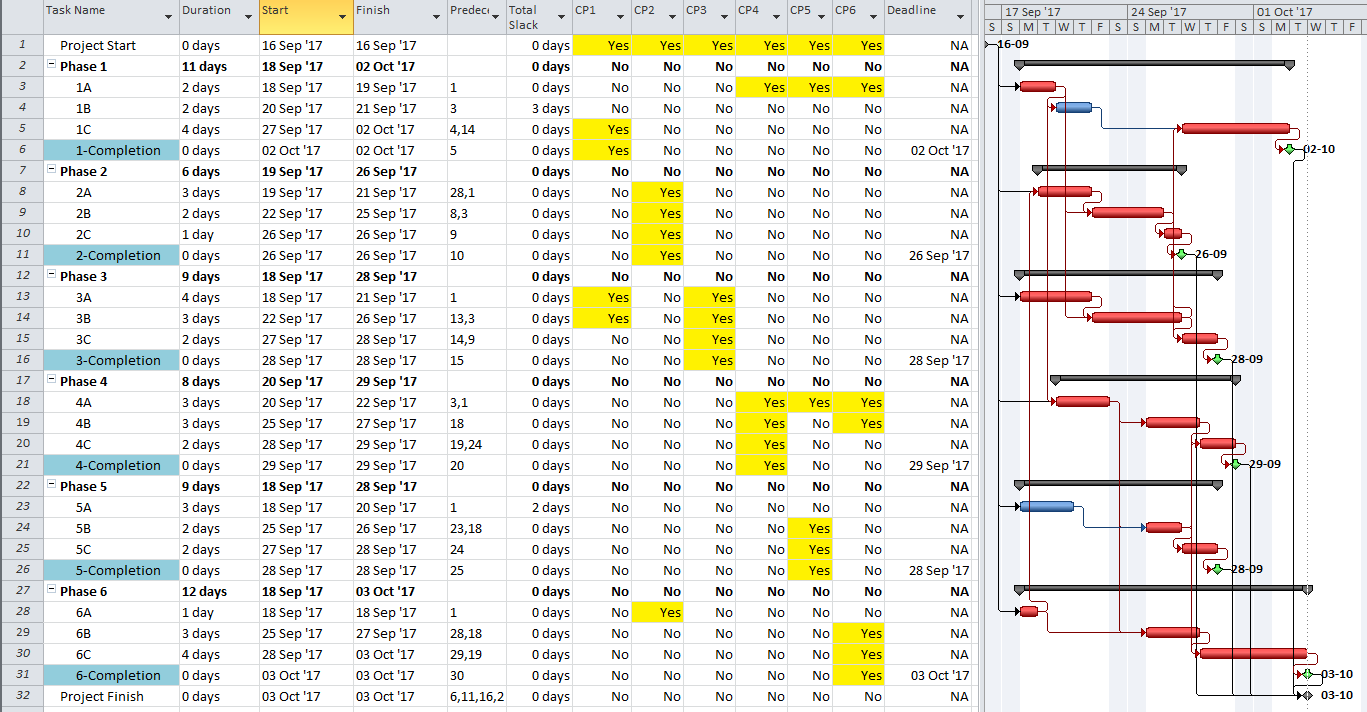
The project is scheduled identically using Oracle Primavera P6 (P6).

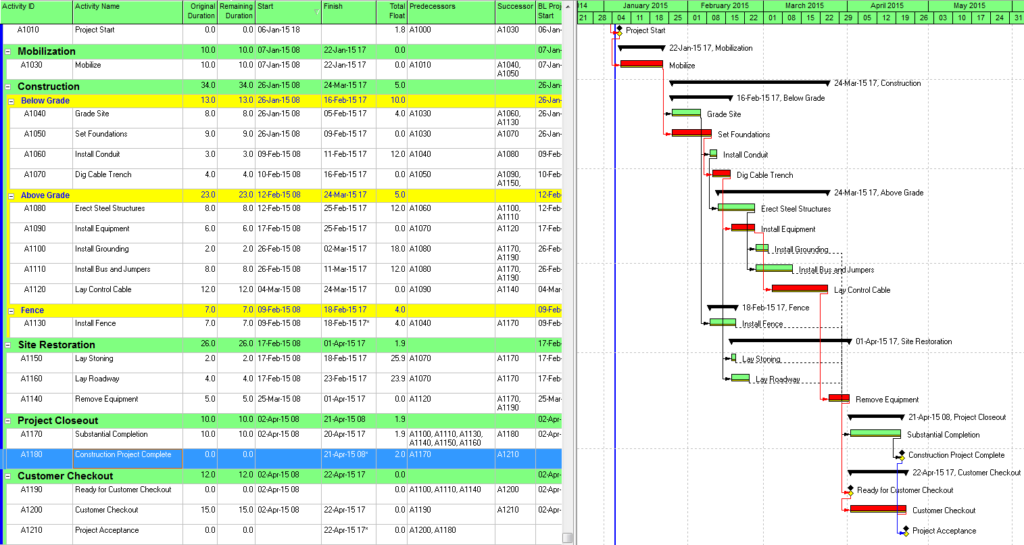
As a result of the modest number of inter-phase relationships, the critical/driving paths for five of the six phases include activities from other phases. The exception, Phase 3, is essentially self-contained, although several of its tasks are also driving the completion of Phase 1.

So, how are these six different critical paths identified?

Identifying Multiple Critical Paths

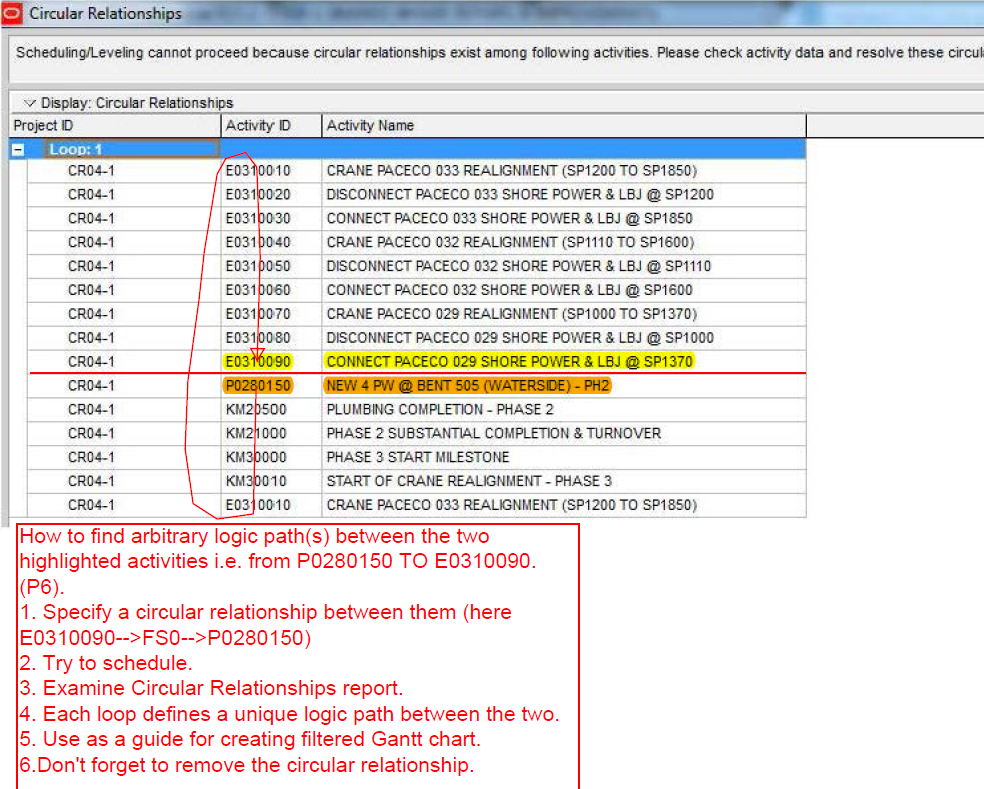
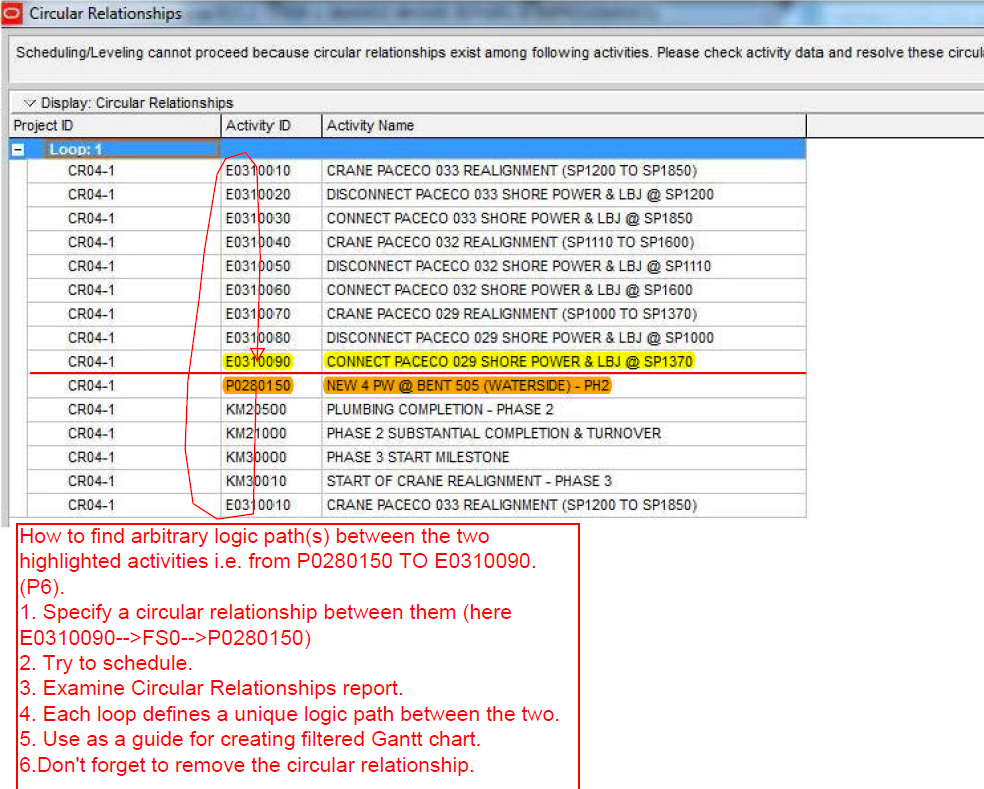
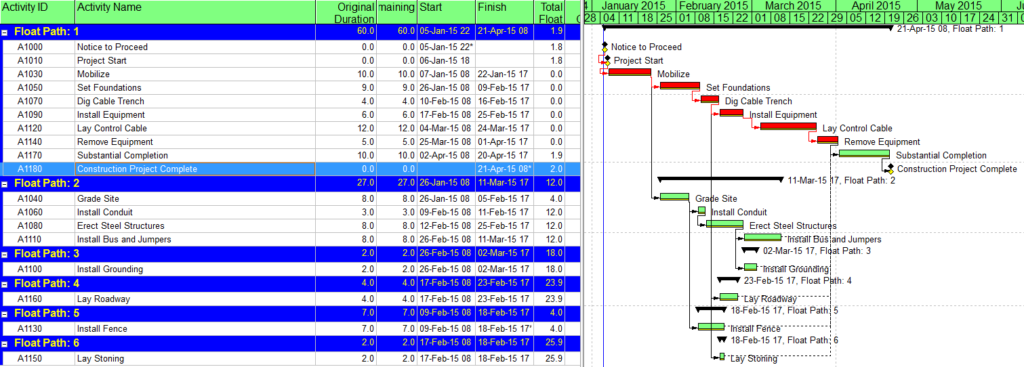
There is in fact no way to simultaneously define the critical paths to each of the six phase completion milestones of the example project using Total Slack alone without manipulation. The paths must be identified individually and directly reported (in the manner of BPC Logic Filter) or manually marked.

Deadlines / Late Constraints

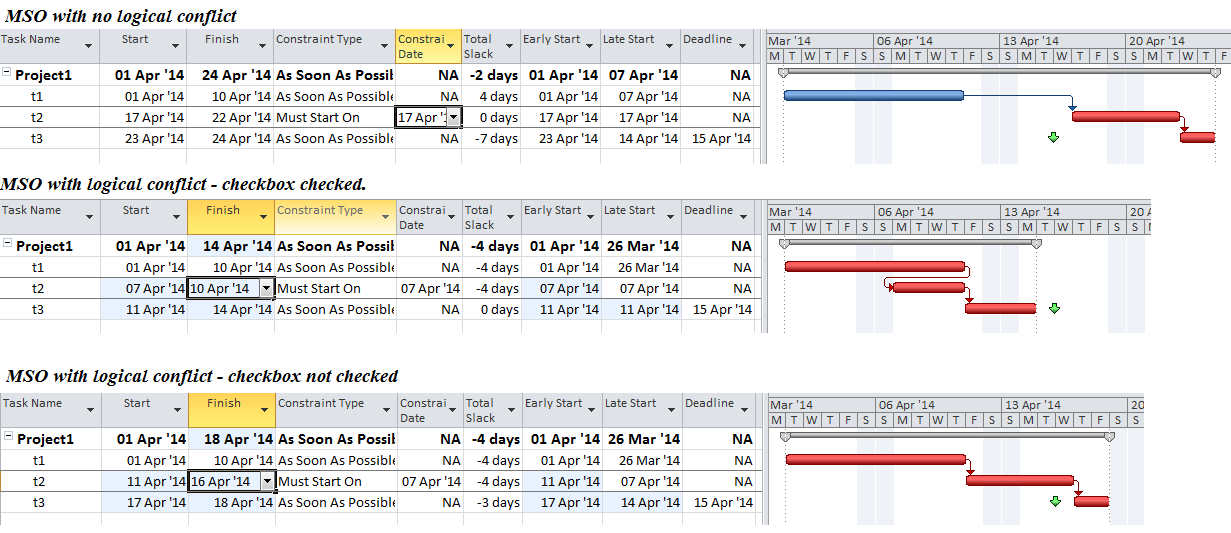
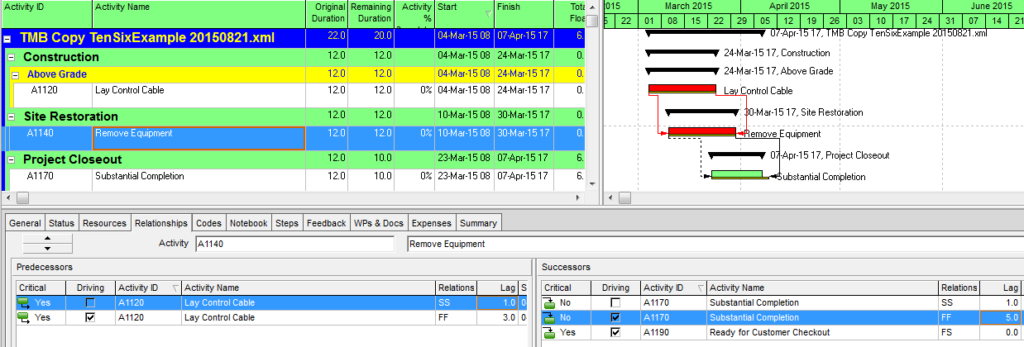
It is common to apply deadlines (or late constraints in P6) to key completion milestones that are contractually defined – typically with financial consequences for delay. Deadlines have the potential to reduce Total Slack/Float, which MSP and P6 use to identify Critical tasks. When deadlines are applied to tasks and milestones that – together with their predecessor chains – are logically and organizationally separate, then Total Slack/Float can provide a reasonable indication of the driving path to each “deadlined” task or milestone. This is a rare circumstance. With only a single deadline applied, the Total Slack/Float for any task will be potentially influenced by the Project Completion date and by the deadline date, with the more “urgent” of the two forcing a lower Total Slack/Float value. With more deadlines and intersecting logic paths, the issue is multiplied.

In the present example, each phase completion task has been given a deadline corresponding to its current finish date. Consequently, all except two tasks in the entire project are given a Total Slack value of Zero and marked “Critical.” The delay of any of these tasks is certain to violate at least one of the deadlines, although the deadlines to be violated are not obvious without the table. The actual driving path to each phase completion remains obscured. Although not completely reliable for defining individual driving paths, deadlines (and late constraints in P6) remain useful for flagging those tasks whose delay could affect (or already have affected) a contractually significant milestone.

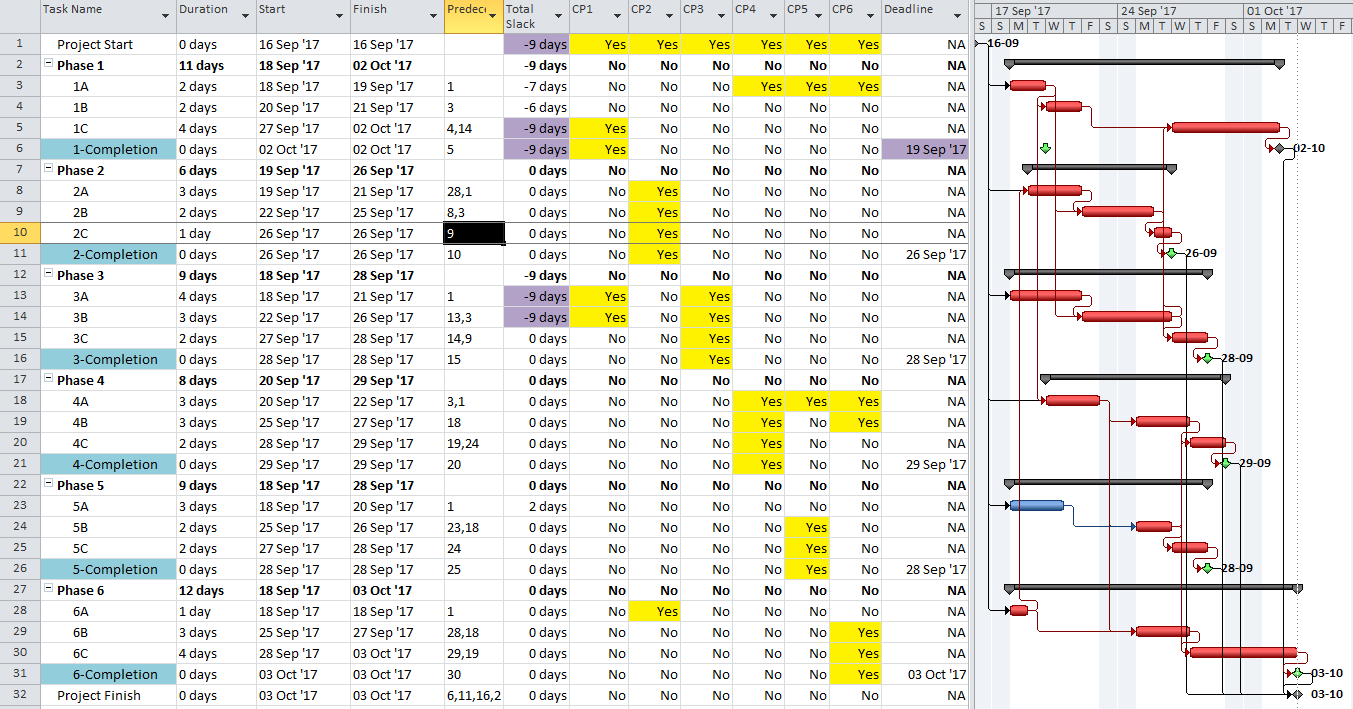
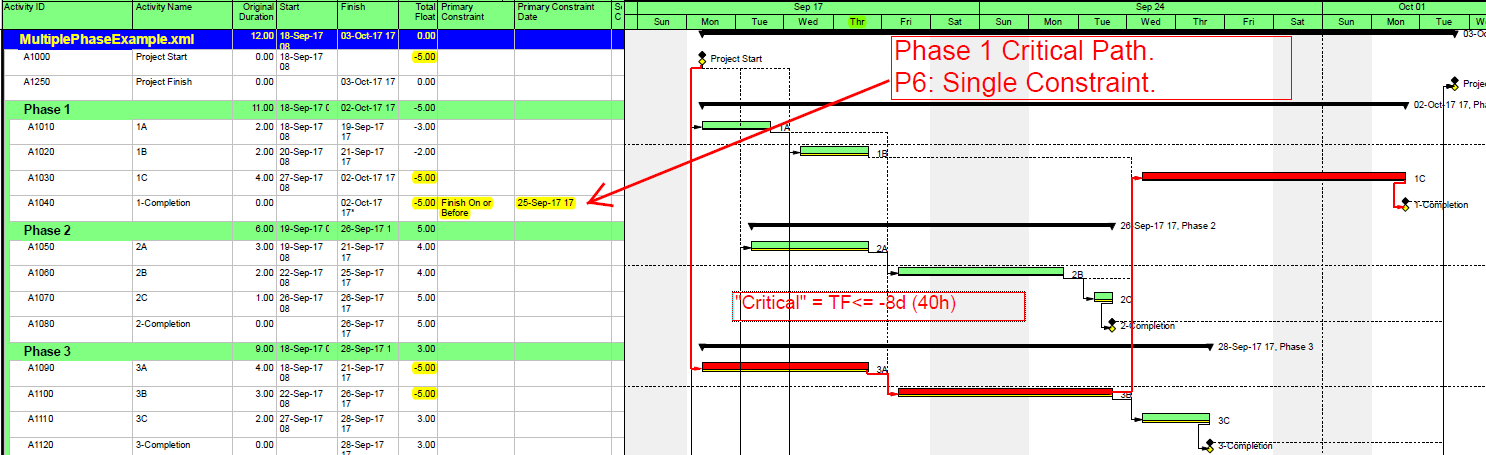
If the project already includes multiple deadlines (for contractually significant milestones), then the critical/driving path for each milestone can be identified (one at a time) by forcing the milestone onto the MOST critical path, i.e.:

Temporarily accelerating the deadline date to the point that it becomes the most “urgent” deadline in the schedule network for all affected tasks. The Total Slack of the milestone and its driving predecessors is then easily distinguished from that of other tasks; and then
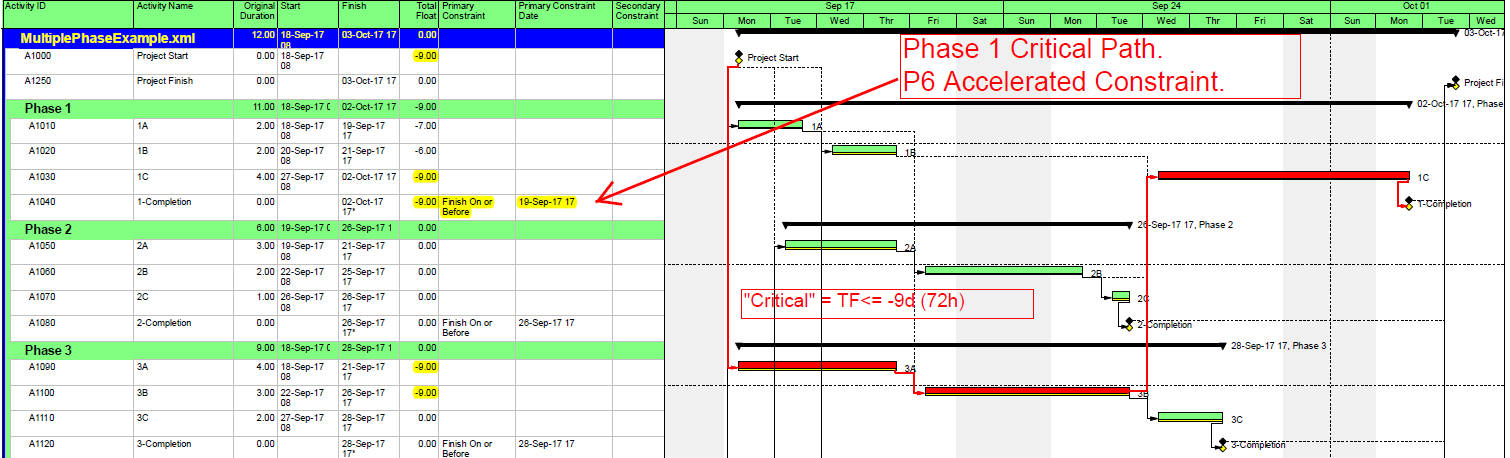
Marking the tasks identified by the lowest Total Slack value. Here, the deadline for the Phase 1 completion was accelerated by 9 work days, resulting in a Total Slack of -9 days for the completion task and its driving predecessors. The CP1 custom flag field could then be marked accordingly.

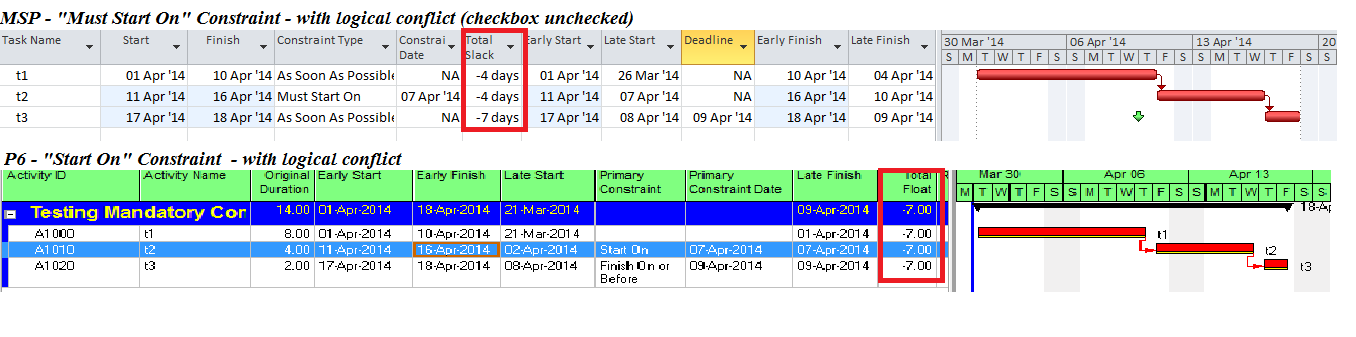
As shown here, a nearly-identical process (using an accelerated Finish-on-or-before constraint) can be used for a P6 project schedule with multiple late constraints.

A similar approach can be used by adding a deadline or late constraint (in P6) if the project has none.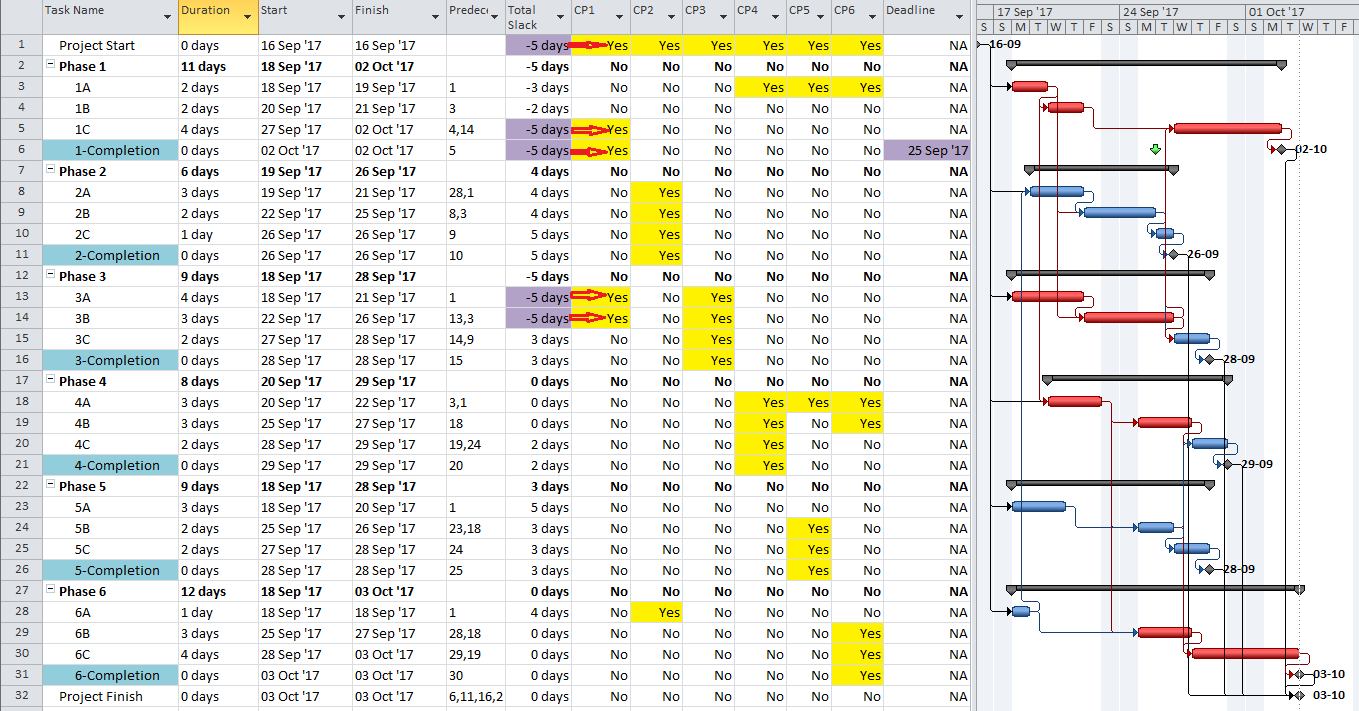

In fact this is the “Constraint Method” that was recognized by the Defense Contract Management Agency (DCMA) as the only valid method for defining a program critical path as part of its 14-point schedule assessment.

As shown above, using deadlines or constraints to generate negative slack/float is an effective way to identify multiple critical paths. In Microsoft Project, however, these paths are difficult to distinguish on the Gantt charts because their red bars are not uniquely differentiated from others. Both MSP and P6 can set the “Critical” flag – resulting in the red bars – for any tasks whose Total Slack/Float is below a certain user-specified threshold. Unlike P6, MSP does not permit this threshold to be less than zero. Consequently, all tasks with negative Total Slack – even those which are not driving anything – are flagged as “Critical” and given the red bar in MSP.

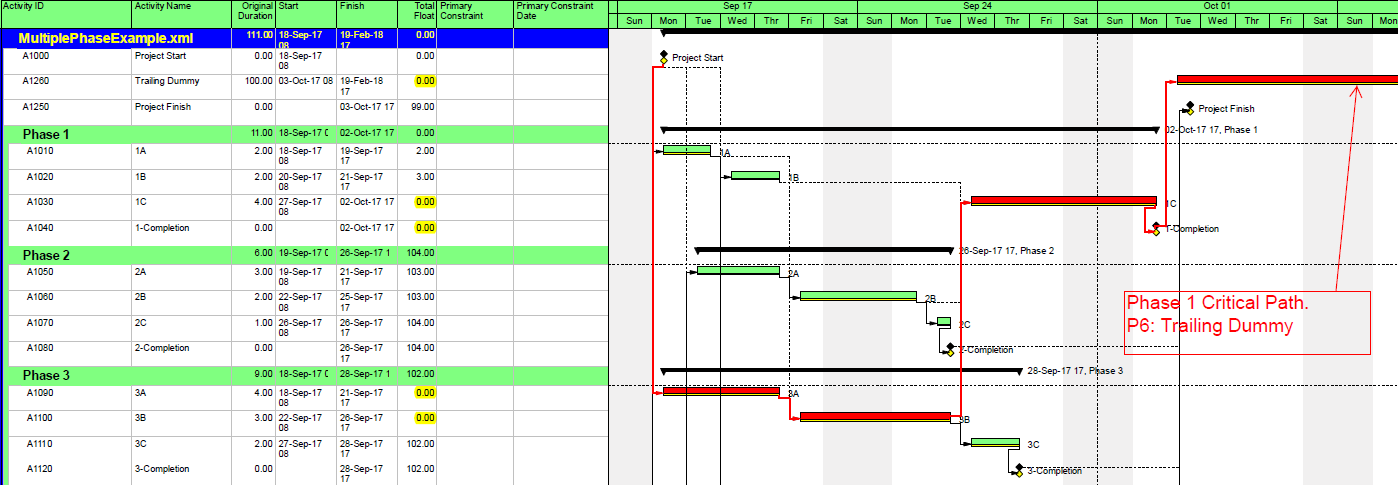
Trailing Dummy

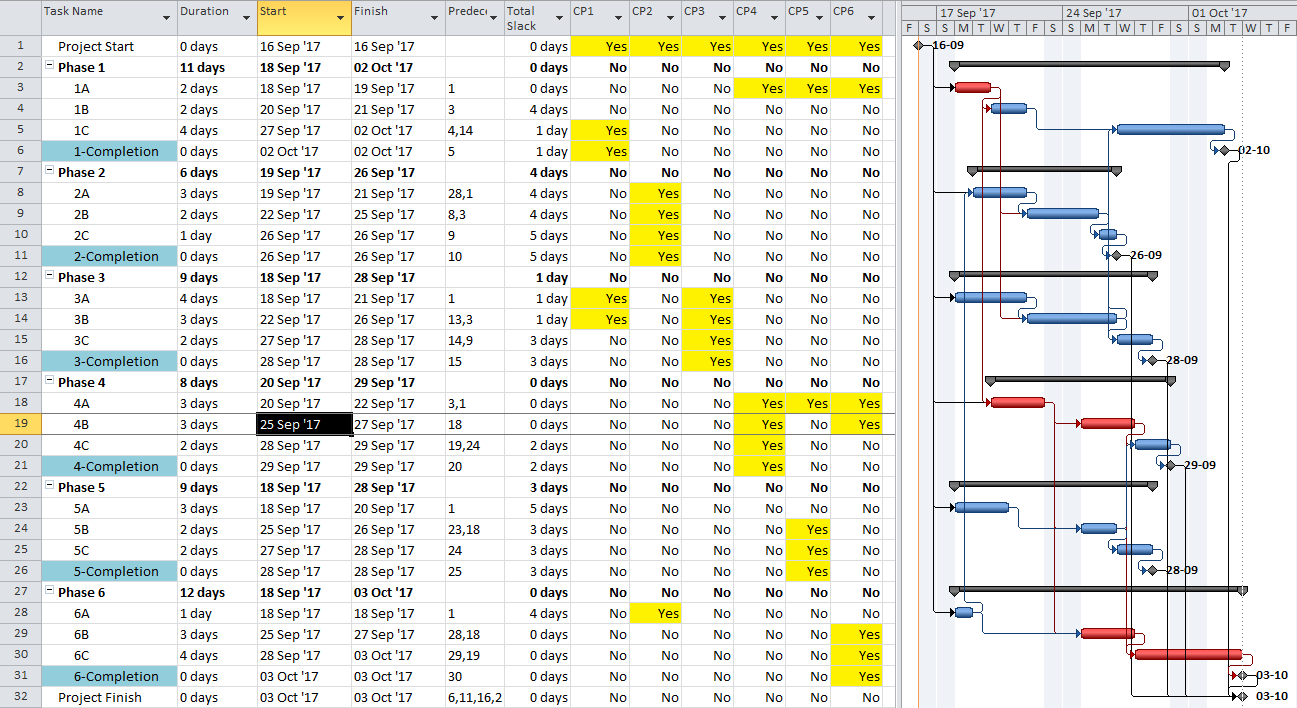
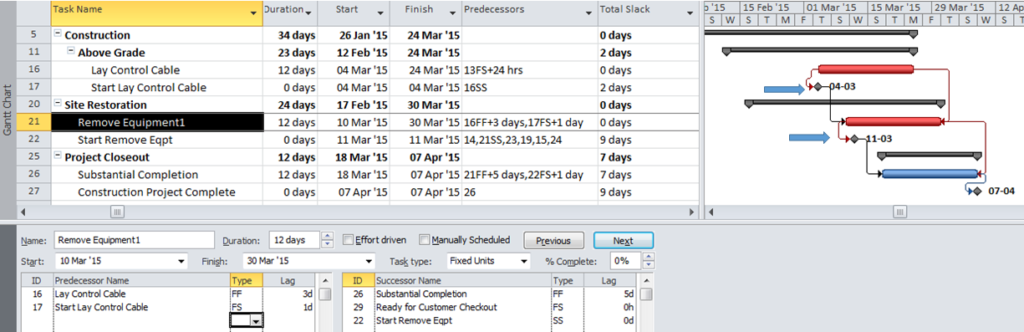
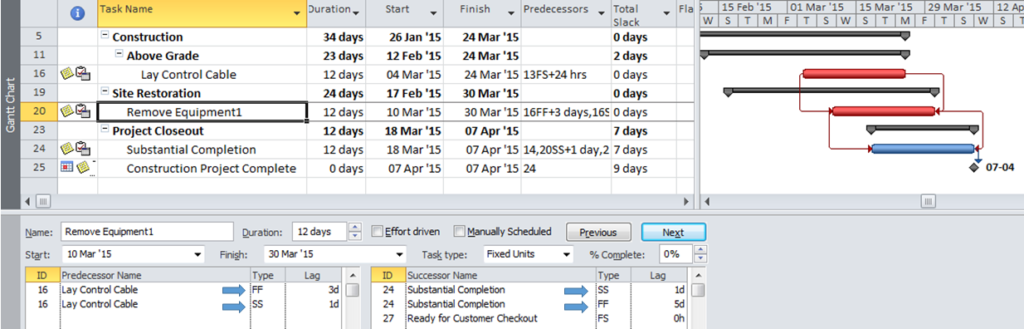
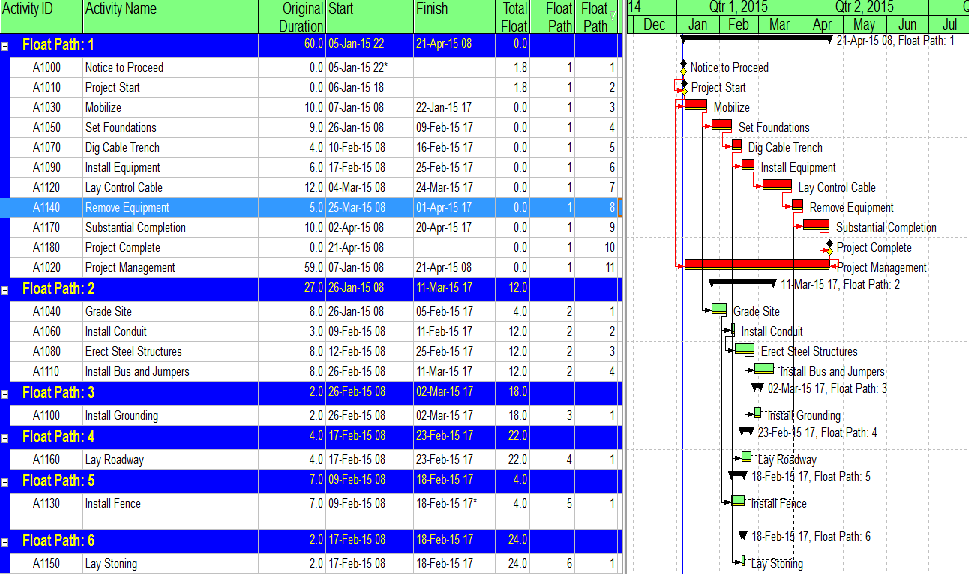
An alternate approach to overcome this limitation for presentation purposes uses a “super-long trailing dummy” task. In this approach, all deadlines and late constraints in the project must be removed (at least temporarily). Then a “trailing dummy” task is assigned as a successor to the first key completion milestone, forcing the milestone onto the critical path. The duration of the trailing dummy must be long enough to extend the completion of the project, creating positive Total Slack for all tasks that are not part of the dummy’s driving predecessor chain. As shown in the following two figures, adding the 100-day Trailing Dummy task as a successor to the Phase 1 completion milestone effectively creates a new critical path for the project – one which is easily recognized as the Phase 1 critical path on the Gantt chart. Moving the trailing dummy successor from phase to phase – one at a time – reveals the unique critical path for each phase.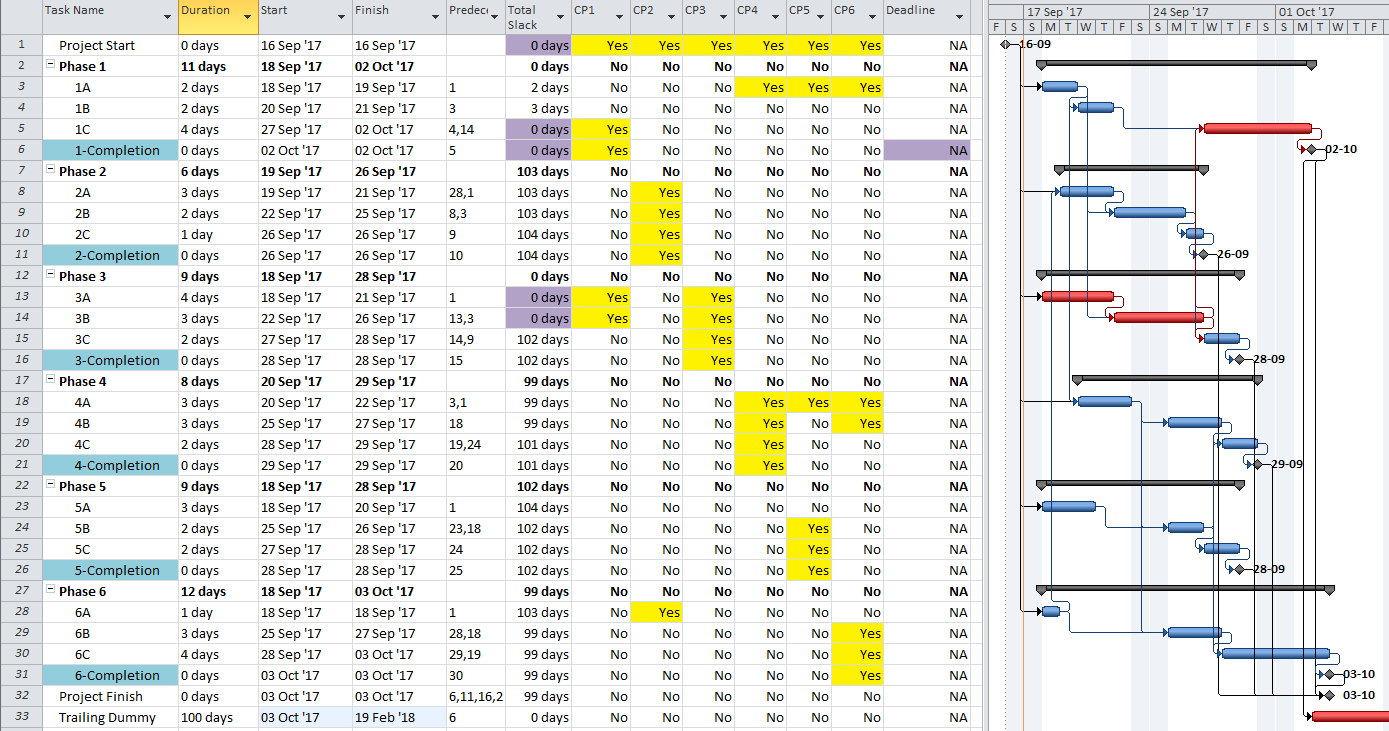

So far all of these approaches rely on temporary manipulation of Total Slack or Total Float, and it is important that such temporary changes be reversed prior to sharing or distributing schedule files. Obviously, these approaches can be labor-intensive and error-prone, making them impractical when the schedule status (and logic) is in flux – as during regular weekly/monthly updating. Even when the complications of multiple deadlines or late constraints are removed, Total Slack also becomes unreliable as an indicator of critical/driving relationships whenever multiple task/resource calendars or resource leveling are applied.

Driving Logic Tracing

The “Longest Path” algorithm in P6 defines the project’s Critical Path by automatically tracing driving logic backward from project completion. This avoids the complications that late constraints and multiple calendars introduce to the interpretation of Total Float, and it is the preferred calculation method when these factors exist. (It is unfortunate that P6 seems to be the only mainstream project scheduling tool to implement it.) Since the algorithm always begins the backward trace with the project completion activity, using it with the trailing dummy method above is useful for identifying multiple critical paths on the basis of driving logic. Driving logic can also be traced in other ways.

Driving Path Trace / Filter (P6)

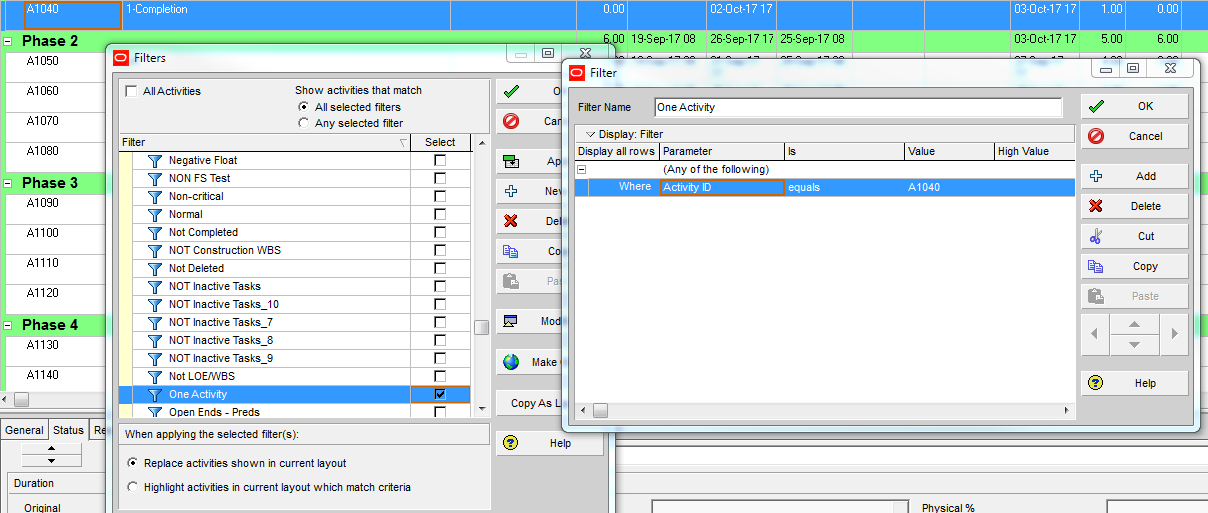
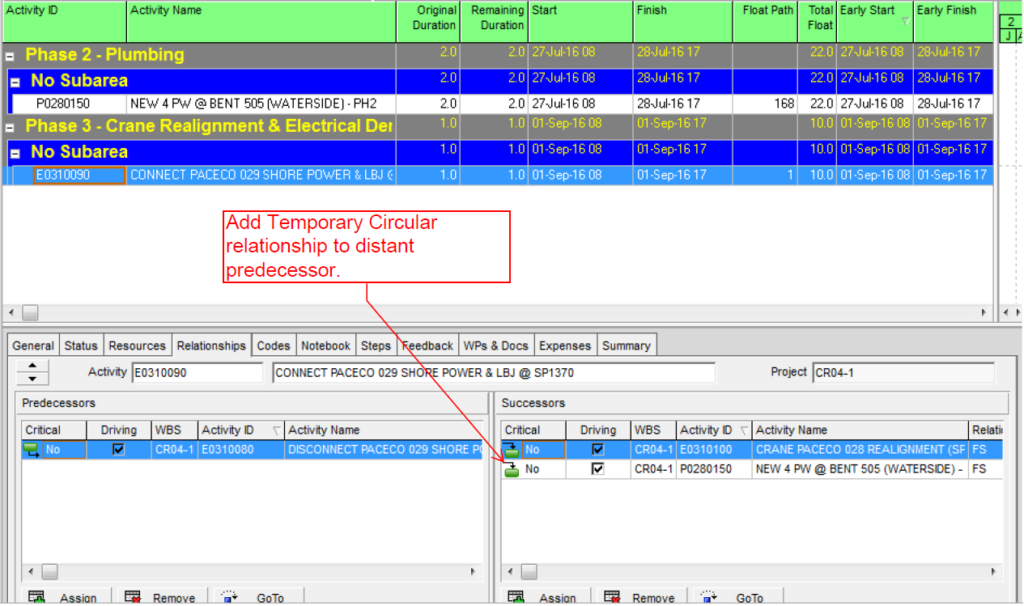
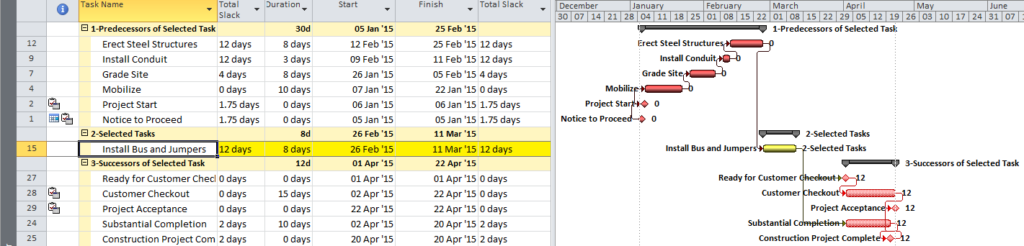
P6 automatically identifies driving and non-driving relationships in the task details. It also allows users to automatically add activities to existing filters by simply selecting them. The combination of these two features allows users to manually construct a filtered view of the critical path to any completion milestone by simply clicking backward through the driving relationships.

The first step is to construct a custom filter to isolate the completion milestone of interest. Here we are focusing on the Phase 1 completion milestone.

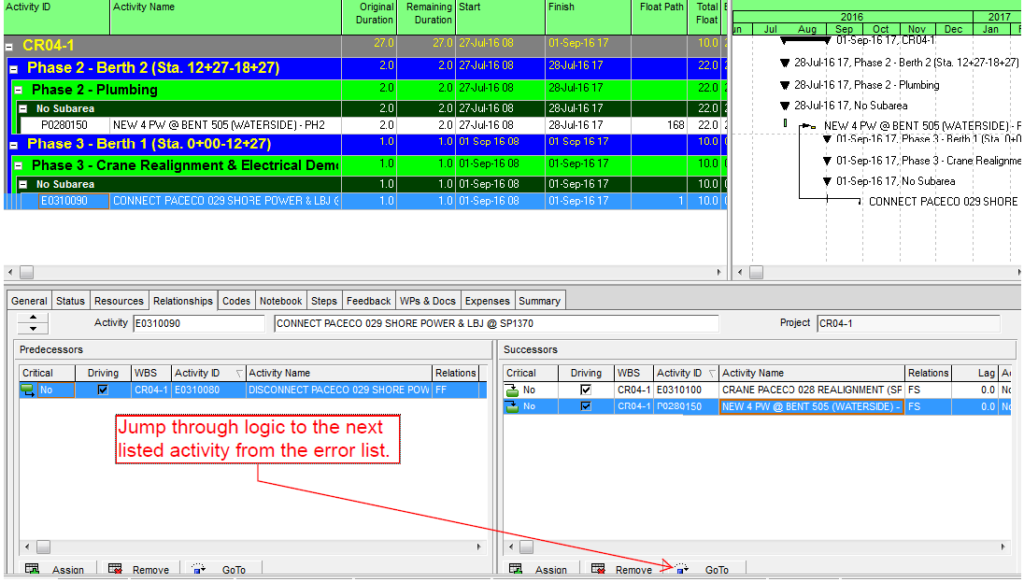
Next, the chain of driving activities (i.e. the driving path) is added to the view by stepping backward through the driving relationships using the “GoTo” button in the predecessors pane. Here is the view after taking the first backward step.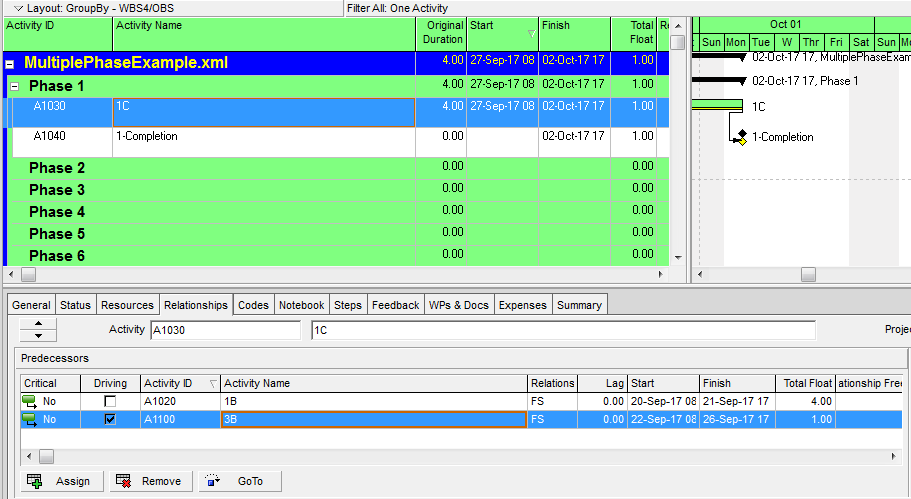

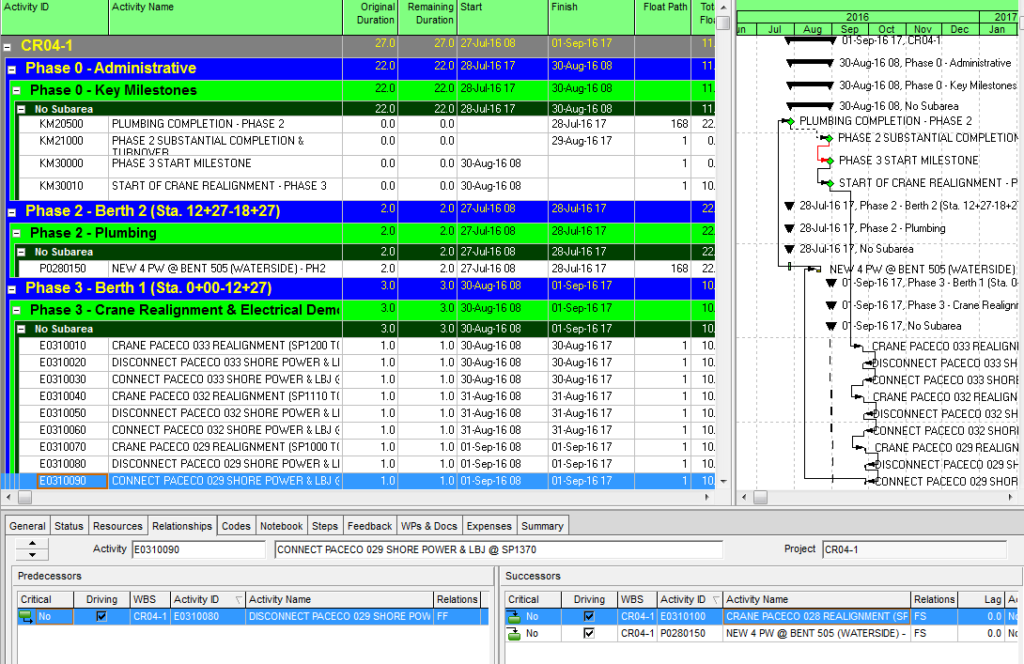
Here is the view after tracing the network all the way back to the first driving relationship. This is the driving (i.e. “critical”) path for the Phase 1 completion milestone.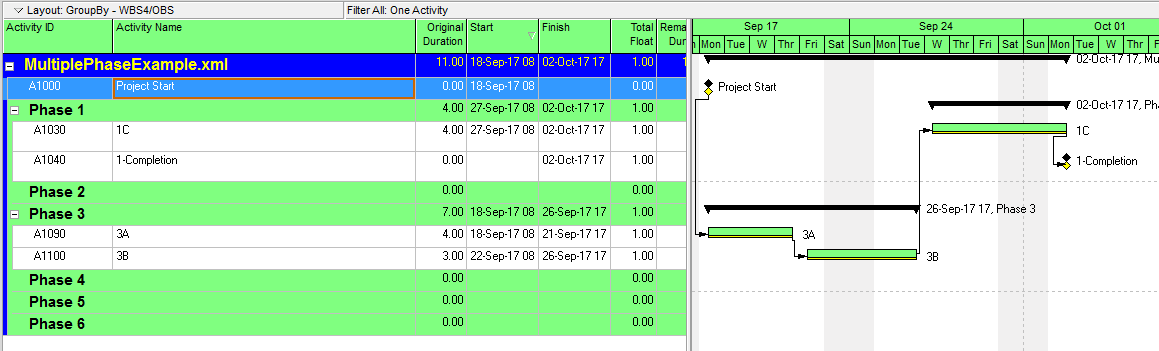

This click-tracing technique can become tedious when the project schedule is complex and there are numerous branches to the logic paths. For example, if an activity along the driving path has two driving predecessors, then the analyst must make a note to return to the second one after the first is fully explored. In addition, P6 routinely marks all links to Level-of-Effort (LOE) activities and links to ALAP-constrained predecessors as driving. The LOE activities must be ignored during the trace, and the ALAP constrained activities need to be evaluated separately. Finally, near-driving logic paths can be identified by the “relationship free float” field in the predecessors table, but isolating driving and near-driving paths involves creating and marking a number of new activity fields.

Fortunately, P6 includes an advanced scheduling option for calculating multiple float paths, which I’ve previously written about here. This option effectively automates the click-tracing technique.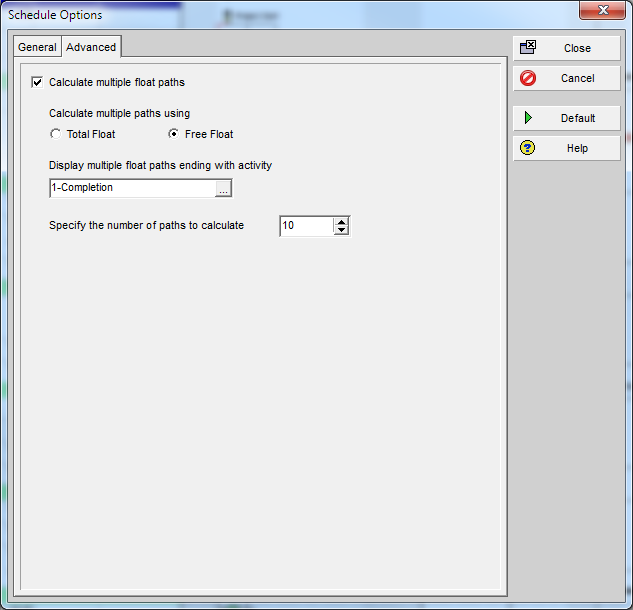

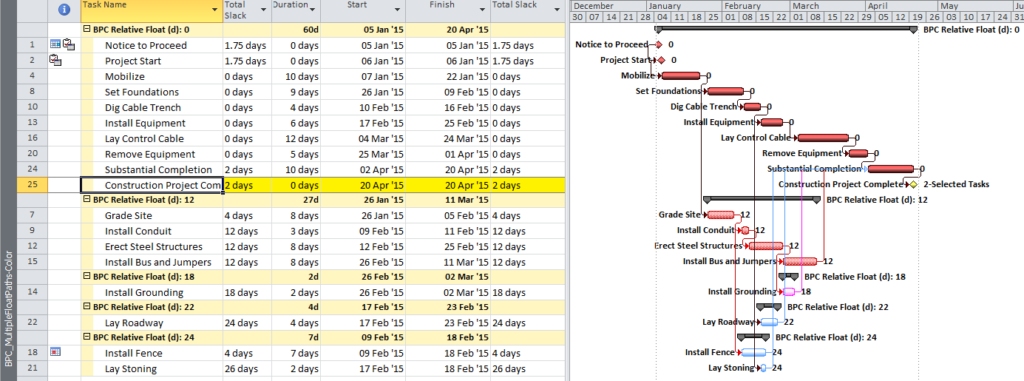
Combined with a view/layout/filter that depicts the “Float Path” field, this option provides a robust and repeatable method for defining the driving and near driving paths to each phase completion milestone in a P6 schedule. (The “free float” option must be used.) Float Path number 1 identifies the (first) driving path. Higher Float Path numbers identify any parallel driving paths and near-driving paths. Like the click-tracing technique, Multiple-Float Path analysis works without modifying the schedule network, so reversing temporary changes is not a concern prior to sharing the schedule. Neither of these techniques affects P6’s assignment of the “critical” flag, however, so red-bars on the Gantt charts are not meaningful.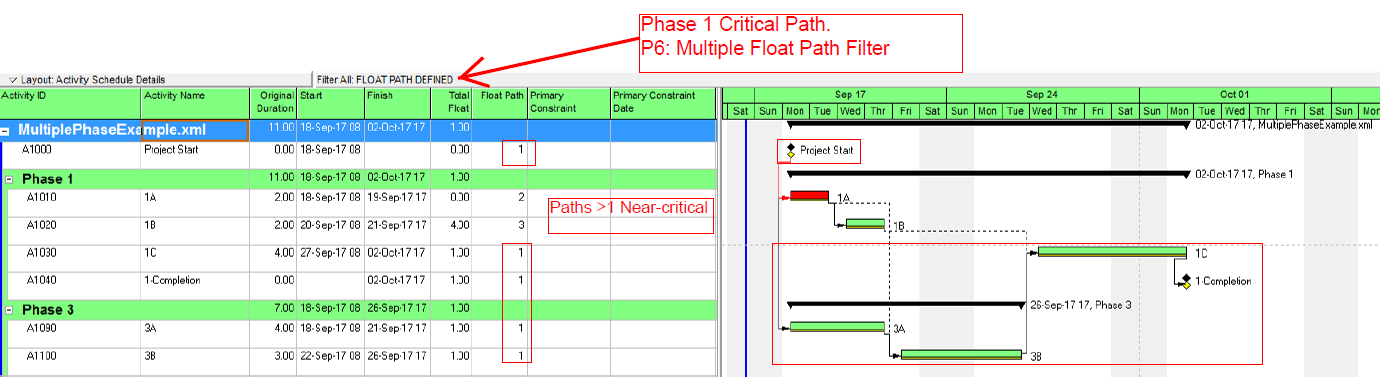

Task Path (MSP)

If you are using a recent version of Microsoft Project (2013+), then the driving path to each phase completion milestone can be visually identified and highlighted on the bar chart using the “Task Path” function with the “driving predecessors” switch selected. (Task ID6 is selected, and the tasks in its “Driving Predecessors” Task Path are highlighted orange.) The user can then manually enter a code (like the custom flag fields shown above) to mark the highlighted tasks. It is fairly straightforward to automate the generation of a task path filter using a macro, and some macro snippets have been published. (E.g. here.) Unfortunately, Task Path’s “Driving Predecessors” are not reliable for most complex projects (e.g. when non-Finish-to-Start links, in-progress tasks, or manually-scheduled tasks are present.) Those issues are discussed in my other blog entry here.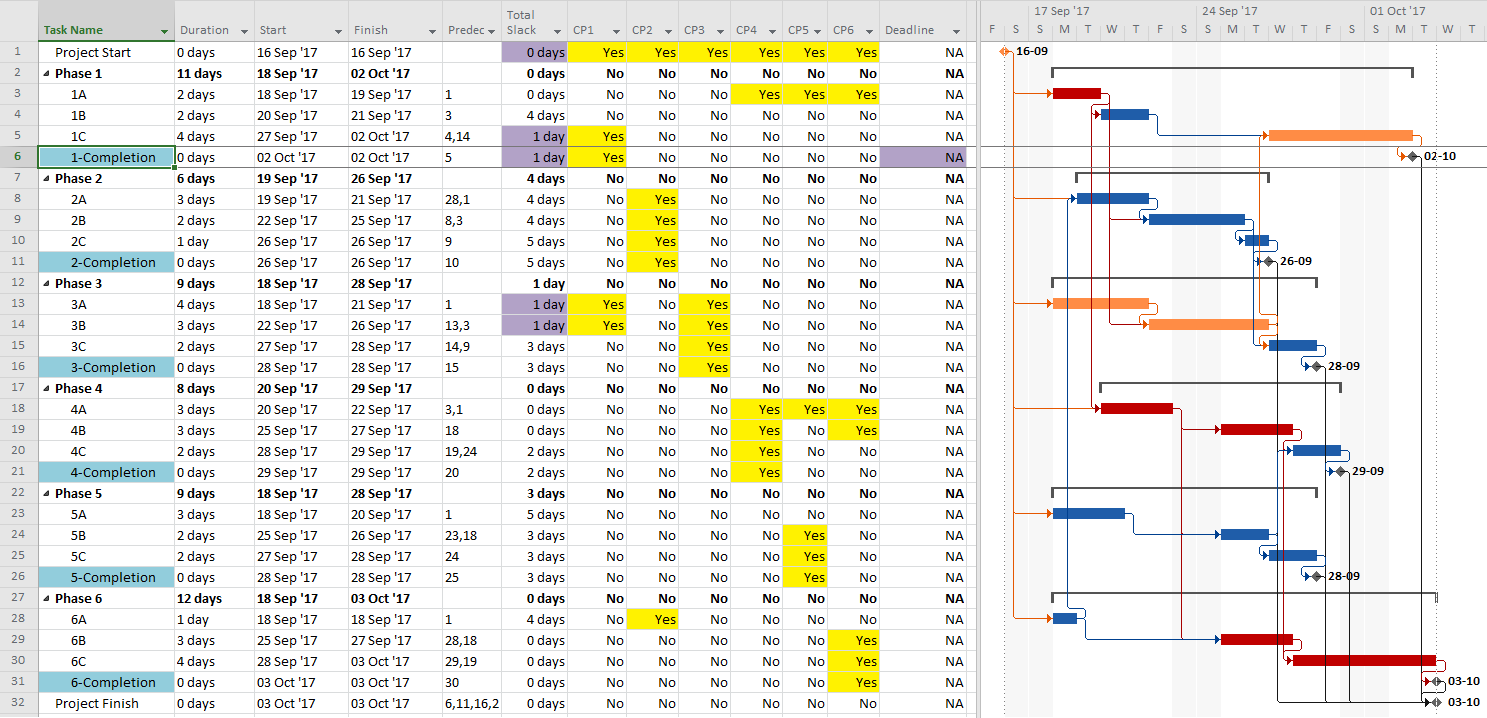

Logic-Tracing Add-ins

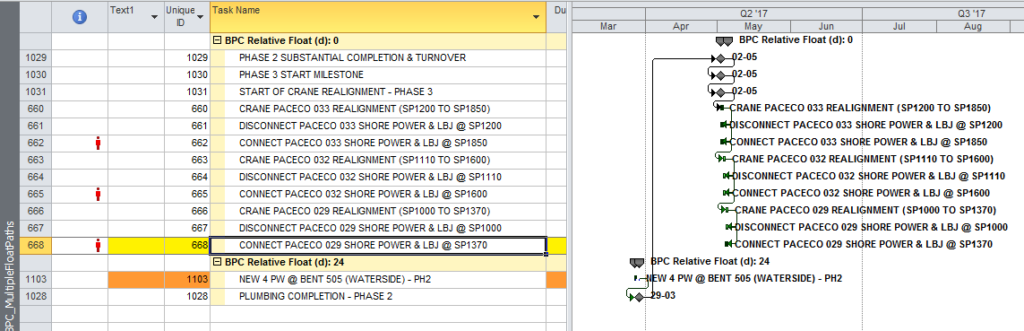
BPC Logic Filter (an MSP add-in) was developed in part to offset the absence of the Longest Path and multiple float path analysis in MSP. The chart below shows driving and near-driving paths to Phase 1 completion – depicted by altering the bar chart. The driving path is indicated by dark red bars with the zero indicating zero relative float. Consistent with the trailing-dummy results, the two non-driving tasks that are part of Phase 1 are depicted as having 2 days and 3 days, respectively, of float relative to the Phase 1 completion milestone. That is, they could slip 2 or 3 days before affecting the milestone. Similar depictions of the driving and near-driving paths for the other five phases, and for the project as a whole, are made possible with a few clicks. Since the schedule network is not manipulated in any way, Total Slack remains unchanged, and there is no need to reverse any analysis-based modifications prior to sharing the data file.

A Note About Open Ends

Some experts have suggested using open-ended logic along with a built-in software calculation setting to automatically mark multiple critical paths. The proposal is as follows:

Ensure that each of the Phase completion milestones is sequenced so that a) it is a logical successor to all the activities in the phase, and b) it has no successors.
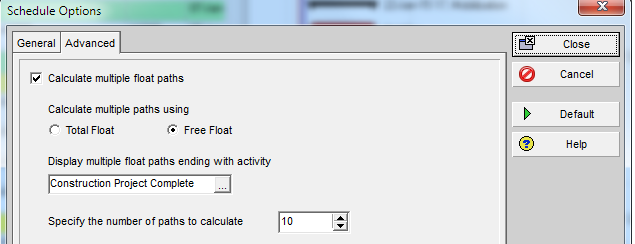
Enable a calculation setting that forces activities with no successors to have zero total float. In P6, this setting is the “Make open-ended activities critical” schedule option. In MSP, the setting is the “Calculate multiple critical paths” advanced calculation option.

Effectively, this is the same as assigning a deadline to each completion milestone at a date that exactly equals its early finish date – an example of which was already explored above. It is subject to the same drawbacks of that approach, but with none of the advantages. I.e. If there are intersecting logic paths between phases (as shown in the example), then which activities are driving which milestone cannot be determined based on total float alone. One merely sees a bunch of zero-float activities in all the phases. Moreover, the basic technique of accelerating the milestone’s deadline/late-constraint date to reveal its driving predecessor path (through negative float) is not available when no deadline or late constraints have been applied. Between this and other failings, I just don’t see any advantages to this open-ends approach.

Recap

A project schedule can possess multiple critical paths for one of two primary reasons:

There is a single key completion milestone at the end of the project, and multiple, concurrent, parallel driving paths to that milestone exist. In this case, the multiple critical paths often reflect a schedule model that is simpler than the actual execution of the project. Correctly accounting for productivity of the assigned resources may remove the apparent concurrency and restore the single Critical Path, but the increased overhead of developing and managing a more detailed schedule would need to be justified.
The project possesses multiple key completion milestones, each with its own legitimate driving/critical path. In this case, the correct identification and status reporting for the multiple Critical Paths is often beyond the capabilities of the scheduling software. Then specialized logic tracing techniques are required.

These factors can also be combined in some project schedules.

Dangling Logic in Project Schedules

Logic Driven project schedules can suffer from two kinds of open-ended or Dangling Logic, which makes the resulting schedule unreliable for dates or float analysis.

Project schedules need robust logical bases to reach two primary objectives:

A schedule that accurately represents a true and achievable plan for executing the work – including technological and resource constraints.
A schedule that supports accurate forecasting of consequences when the work does not proceed as originally planned – for example when activities fail to start or finish on time.

Dangling Activities – CPM

Logic-driven scheduling – often generically identified as “Critical Path Method” (CPM) scheduling – determines schedule dates by enforcing stringent logical sequential relationships between tasks from the start to the finish of the project. The definition of adequate scheduling logic depends on the details of the project. Logic is clearly inadequate, however, if any activity in the schedule is left logically disconnected from either the project start or the project finish – i.e. the activity is left “dangling.” In the simple network diagram shown below, four activities are shown with no predecessors, while one activity is shown with no successors. These cases typically represent omission of legitimate logical relationships with other (latent predecessor/successor) activities. As a consequence, the early and late dates – and the Total Float – of all potentially-connected activities are not reliable. The objectives of the logic-driven schedule can’t be met. As a general rule, every activity in any CPM schedule – except the start and finish milestones – must have at least one predecessor and at least one successor. Dangling activities not meeting this rule – also known as open-ended activities, “hanging activities”, or simply “hangers” – indicate inadequate schedule logic.

Dangling activities that are missing predecessors and/or successors are relatively easy to isolate in project scheduling tools – including Microsoft Project (MSP) and Oracle Primavera P6 (P6) – by using an activity filter that searches for empty “predecessors” or “successors” fields. It is common for experienced schedulers to routinely tie such dangling activities to general-purpose milestones such as “notice to proceed” (as a predecessor) or “substantial completion” (as a successor). Such an approach removes the obvious indication of inadequate logic. Close review of the relationships at such “merge points” in the schedule may still be necessary to identify activities whose true predecessors and successors are not sufficiently defined.

Dangling Activities – PDM

Most modern scheduling software implements a variation of CPM scheduling called the Precedence Diagramming Method (PDM). In addition to the “Finish-to-Start” relationship of basic CPM scheduling, PDM allows “Start-to-Start,” “Finish-to-Finish,” and “Start-to-Finish” relationships, all with or without lags. While PDM software allows more realistic and more efficient modeling of real-world project schedules, it is possible for activities to have both predecessors and successors yet still suffer from dangling – hence inadequate – schedule logic. These cases – generally categorized as dangling finish and dangling start – are also known as “orphan relationships.”

Dangling Finish

Consider the following three activities taken from a conceptual schedule for a civil construction project. The project will take place on land that has been intentionally surcharged (pre-loaded with piles of soil) to strengthen the underlying materials. The conceptual plan for the three activities is simple: 1) Push/roll-off the surcharge material to adjacent areas; 2) Perform grading and quality-assurance testing of the ground; 3) Construct concrete foundations for the buildings.

Because these activities are spread over a large area, it is possible to start the grading before completing the roll-over and to start the foundations before completing the grading. The scheduler has modeled these relationships (in MSP) as SS+50% – that is the successor may start only after the predecessor has started, but with an additional lag of 50% of the predecessor’s duration (computed according to the successor’s calendar). These activities, relationships, and the resulting (early) scheduled dates seem to reflect a true and achievable plan for prosecuting the work, meeting the first objective of a logic-driven schedule.

If the activities fail to progress as initially planned, however, then the schedule may not accurately forecast the consequences. If the Roll-Over takes longer than expected, then this delay may in fact affect completion of the Rough-grading task and, eventually, the foundation construction and its successors. The schedule model fails to account for these extended finishes, however, and may forecast outcomes that are physically impossible – such as building foundations being constructed in areas where the surcharge material has not yet been removed.

When the indefinite delay of an activity’s finish has no logical consequences for any other activity, then the activity has a “dangling finish” – representing incomplete logical development of the schedule. In a PDM schedule, any activity with ONLY SS or SF successors has a dangling finish. Such dangling finishes are called “open finishes” in Acumen Fuse, a 3^rd party diagnostic tool.

Dangling Start

The same three activities could be modeled instead using Finish-to-Finish relationships to arrive at identical dates.

If subsequent schedule developments lead to longer durations for successor activities, the schedule model will respond by having them start earlier. As a consequence, some schedule dates may occur at times that are physically impossible – such as starting rough grading before the first shovel of surcharge has been removed or (again) building foundations being constructed in areas where the surcharge material has not yet been removed.

When the indefinite acceleration of an activity’s start may be implemented without logical restraint from any other activity, then the activity has a “dangling start” – representing incomplete logical development of the schedule. In a PDM schedule, any activity with ONLY FF or SF predecessors has a dangling start. Such dangling starts are called “open starts” in Acumen Fuse.

Correction of Dangling Starts/Finishes

The examples shown are typical of overlapping activities with progressive feed relationships. In such cases, it is common to implement a “ladder logic” scheduling model, where multiple parallel Start-to-Start and Finish-to-Finish relationships are imposed between related activities. Such a model is easy to implement in P6. In MSP – which prohibits parallel relationships between tasks – then dummy milestones are needed.

In a schedule model incorporating ladder logic, one of the two parallel relationships will drive the successor’s dates, depending on the relative durations and lags. In the example below, the Rough grading activity is driven by its Start-to-Start relationship with Roll-over. Because Rough grading has been extended, however, the subsequent Foundations construction is delayed (and driven) by the Finish-to-Finish relationship from Rough grading. This represents robust logic development between the activities.

In general, dangling starts/finishes are avoided by explicit inclusion of all legitimate technological and/or resource constraints in the schedule model, even where the resulting relationships are not obviously driving successor activities. This is, of course, the basis of all robust logic-driven scheduling practice.

Finding Dangling Starts/Finishes

Until recently, detecting and isolating dangling starts and finishes was not an easy process for users in either MSP or P6. In both tools, the preferred approach is to specify an activity/task filter to show only those activities that:

For Dangling Starts –
- Have some predecessors, and
- Have NO FS or SS predecessors.
For Dangling Finishes –
- Have some successors, and
- Have NO FS or FF successors.

In MSP, each task includes a “predecessors” field listing the Task ID, relationship type, and lag for each predecessor relationship. The task “successors” field lists the same information for successor relationships. Unfortunately, the default relationship type – FS – is not explicitly listed in either field, and preparing a filter to exclude activities that contain FS relationships in one field or the other is not trivial, requiring several intermediate calculations. Alternately, the user is left to manually inspect the predecessors and successors of each task, to export the project to Excel for analysis, or to use an add-in like Acumen Fuse or BPC Logic Filter to identify danglers. [The add-ins examine the underlying relationship objects in the MSP database, which could also be done directly using a Project macro/vba.]

Similarly, each activity in a P6 schedule includes both “Predecessors” and “Successors” list fields, but these lists include only the IDs of the connected activities – relationship types are excluded. P6 16.1 and later releases include two additional fields – Predecessor Details and Successor Details – that include relationship types and may be easily included in a filter specification using the above criteria. Users who have not updated to P6 16.1 or later – and who do not have access to an add-in like Acumen Fuse or Steelray – may export the activity and relationship information to a spreadsheet for analysis. (Spreadsheet analysis of the P6 data is generally more straightforward than for MSP.)

Consequences of Dangling Logic

The primary consequence of dangling logic in a project schedule is an initial/Baseline plan that is not reliable due to the omission of substantial sequential constraints. For example, many fast-track design-build projects require the start of field work before the completion of engineering, and sometimes the final engineering works are either left dangling or are tied only to a generic project completion milestone. The logical ties between certain engineering activities and the necessary quality assurance and commissioning activities may be inadvertently omitted. Without complete logic, neither the early (CPM) dates nor the late dates for the project are reliable. Total Float shown for the later engineering activities and for their latent/unlinked successors may be excessive. Since Total Float and the Critical Path definition are unreliable as a result of missing logic, the Baseline project schedule does not provide a suitable basis for monitoring progress or for evaluating potential delays.

Many project schedules may appear acceptable at the time of Baseline review, but dangling starts and finishes can severely compromise their usefulness during the project execution. This is ultimately because actual durations invariably differ from baseline durations, but the secondary relationships that are needed to ensure logic integrity are missing. In other words, the schedule model fails to reflect the real consequences of activity delays that appear during schedule updates. The flaws in the schedule logic become obvious, and credibility is lost.

Schedule Risk Analysis is aimed at quantifying, typically through simulation, the consequences of uncertainty in schedule durations. Since the intent of a simulation is to repetitively reproduce the consequences of changed durations in the schedule, the model weaknesses that affect the schedule update process also affect the outcome of the simulation. Therefore, risk simulation of a project schedule with dangling logic is not reliable.

Terminology for Dangling Logic

Dangling logic – and particularly dangling starts and finishes – have been identified as such in the literature for at least 10-15 years. See http://www.projectrisk.com/white_papers/The_Problem_with_Dangling_Activities_in_Project_Schedules.pdf.

Although the two concepts of dangling logic described here (i.e. the CPM and PDM varieties) are fairly straightforward, there is not uniform agreement on the terminology.

The Practice Standard for Scheduling, Second Edition (2011), published by the Project Management Institute (PMI) limits its “dangling” logic discussion to the PDM variety. It describes “dangling” activities as activities that don’t “have an FS or SS predecessor and an FS or FF successor.” In this standard, “Open-Ended Activities” include those “lacking either a predecessor or a successor or both.” Thus, while not explicitly stated, “Open-Ended Activities” are a subset of dangling activities.

PMI’s Scheduling Excellence Initiative Committee has described a dangling activity somewhat vaguely. The Committee’s CPM Scheduling for Construction: Best Practices and Guidelines (published by PMI, 2014) provides the following definition – “Dangling Activity: An activity tied from only one end (start or finish). A dangling activity has only a predecessor(s) or successor(s), not both.” This definition clearly combines the two concepts without distinguishing between them. “Dangling” references in the text are limited to the CPM, or open-ends, concept.

CPM in Construction Management, Eighth Edition (2016), a graduate-level textbook and respected reference book for serious construction planners and schedulers, contains only a single reference to “dangling activities” as something to be precluded. It does not otherwise describe or define them. The book briefly discusses dangling starts/finishes as a problem unique to PDM schedules, but it uses the term “orphaned relationships” rather than “dangling”.

The US’s Government Accounting Office (GAO) and Defense Contract Management Agency (DCMA) both align with the PMI practice standard, describing dangling activities according to the PDM concept. From GAO-16-89G, Schedule Assessment Guide; Best Practices for Project Schedules (2015) – “Dangling activities: number of remaining detail activities and milestones with no predecessor on start date” and “Dangling activities: number of remaining detail activities and milestones with no successor off finish date.” (As of the 21Nov’09 revision, DCMA’s 14-Point assessment guidelines provide comparable definitions and a “general rule to avoid Dangling Activities” under Metric #1: Logic. They are NOT explicitly included in the metric, however.) Open-ended logic (i.e. the CPM variety of dangling logic) is simply identified as “missing logic,” “missing predecessors,” or “missing successors.” This is the source of DCMA’s Metric #1.

The Planning & Scheduling Excellence Guide (PASEG v3, 2016), published by the National Defense Industry Association, includes a brief section on Open Ended Tasks among things to avoid in its chapter on Horizontal Traceability. This section mentions “dangling logic” (specifically a dangling finish) as something to be avoided because it invalidates schedule risk assessment. Neither term is formally defined in the guide.

AACE International (formerly the Association for the Advancement of Cost Engineering) publishes a number of recommended practices (RPs) related to project scheduling. Unfortunately RP 10S-90: Cost Engineering Terminology (which is routinely updated to reflect the development of related standards and RPs) includes a definition for “Open-Ended Activities” only. It ignores dangling logic of the PDM variety.

Dangling Logic in BPC Logic Filter

Users of BPC Logic Filter for Microsoft Project can execute the Project Logic Checker to isolate dangling logic and other issues affecting project schedule integrity. The PMI/GAO definitions are used. This figure shows the same schedule depicted in the network diagram at the beginning of this post – after running the Project Logic Checker. The five “No Predecessors” and two “No Successors” tasks (including start and finish milestones) are clearly tagged and summarized, as are two dangling-finish tasks.

Mandatory Constraints in Microsoft Project and Primavera P6

Here I review some impacts of “hard constraints” on the calculation of total float (or total slack) in logic-driven schedules.

First a Note on Defining “Soft” and “Hard” Constraints

Some project scheduling guidance documents routinely categorize date constraints as either soft or hard depending on their ability to contradict or override network scheduling logic. Mandatory date constraints — must-start-on (MSON) and must-finish-on (MFON) — are uniformly considered hard constraints because they can impose schedule dates that cause logic restraints to be violated. As a result, the logic flow through the network is obstructed. Early date constraints — start-no-earlier-than (SNET) and finish-no-earlier-than (FNET) — are uniformly considered considered soft constraints, presumably because they act in addition to, never in opposition to, the logic.

Both the DCMA 14-Point Assessment guidance (Nov’11) and the GAO Schedule Assessment Guide (Dec’15) also list late date constraints — start-no-later-than (SNLT) and finish-no-later-than (FNLT) — as hard constraints, even though they do NOT cause violations of logic restraints in most scheduling software. The reason for this is unclear, though it may be related to the default “tasks will always honor their constraint dates” setting in Microsoft Project. Under normal scheduling, this setting automatically converts a late date constraint to a mandatory constraint when it creates negative slack/float. Another document (Planning and Scheduling Excellence Guide – PASEG v.3 – from the National Defense Industry Association) seems to recognize this issue, stating “Hard constraints do not allow the logic to drive the schedule (i.e. either restricts all movement or restricts movement to the right) on the constrained task.” In this context, “restricts movement to the right” describes the impact of the setting on early dates (i.e. the default Start and Finish dates) in MSP. Unfortunately, the DCMA 14-Point Assessment guidance continues to equate negative float with the existence of a hard constraint. Such a position seems unsupported by any consistent set of base principles.

Microsoft Project

A recent discussion on technet raised the issue of slack/float calculation for tasks with hard constraints – in this case Project’s “Must Start On” (MSO) constraint. A novice user of Microsoft Project (MSP), was puzzled by MSP’s calculation of non-zero total slack for an MSO-constrained task who’s early and late dates were the same. That is, the expected definition of Total Slack as “Late Finish minus Early Finish” [*] was clearly NOT being followed.

*[The traditional CPM definition of Total Slack/Float is TS=LF-ES-Dur. When Duration is a constant (as in MSP and P6) this simplifies to:

TS=(LF-Dur)-ES ==> TS=LS-ES, and

TS=LF-(ES+Dur) ==> TS=LF-EF.]

Consider the simple example comprising a three-task schedule with an MSO constraint on the second task and a deadline (a soft late constraint) on the third task, which I’ve shown below.

There are two basic issues about MSO (and MFO) constraints in Microsoft Project that come into play:

Under typical default conditions, Project sets both the early start and late start equal to the MSO constraint date. This completely blocks logic flow through the task, and TS is zero. I’ve illustrated this in the first chart below, where I’ve set a lenient MSO constraint on task t2 but imposed a deadline on the completion task t3 to create some negative slack. Clearly the first task t1 should have negative slack, but the backward pass calculations don’t show it.
If the early start imposed by the MSO constraint precedes the early start derived from the forward pass (i.e. the logic), then a logical conflict is created. If the “Tasks will always honor their constraint dates” box is checked in the Schedule options (the default condition), then Project keeps the imposed early and late starts – violating the CPM logic – and “resolves the conflict” by over-writing Total Slack with a negative value. This case is presented in the middle chart below. If the checkbox is not checked, then the Early Start is allowed to slip with the logic while the Late Start is retained. I’ve shown this on the bottom chart.

The example presented is a “Mandatory Constraint,” which is strongly discouraged in general and is explicitly prohibited in many contexts. Unchecking the “Tasks will always honor their constraint dates” box softens the impact of the constraint, but logic flow through the task is still interrupted. Because of these issues, users of MSP would be well advised to avoid MSO or MFO constraints in any context where scheduling logic (and Total Slack) are important.

MSP/Primavera P6 Comparison

With the checkbox checked (i.e. default conditions), Microsoft’s “Must Start On” constraint seems to behave almost identically to P6’s “Mandatory Start” constraint.

Like Project’s MSO, P6’s Mandatory Start constraint over-writes early AND late dates, thereby imposing a null Total Float and interrupting logic flow through the schedule.
In the absence of a logical conflict, Mandatory Start (in P6) results in the same dates AND Total Float (null-value) as MSO in MSP.
There is one minor difference. Whereas Project separately computes and imposes negative Total Slack (on the constrained task only) to highlight a logical conflict, P6 preserves the CPM-defined Total Float of zero on the constrained activity. (This was the basis for the original question on technet.) Both constraints impose negative slack/float on the predecessors of the constrained task/activity based on the logical conflict alone; negative slack/float from a more stringent constraint later in the project will be blocked.

With the checkbox un-checked, the resulting MSP schedule appears similar at first to P6’s schedule when using a (softer) constraint like “Start-On”. This should not be misinterpreted. As shown in the next chart, MSP continues to over-write the late date with the constraint date, even when the CPM-based late date is more restrictive. Resulting predecessor slack values may be incorrect. P6’s “Start On” constraint, on the other hand, results in a correct float calculation for the imposed conditions.

Eddies and Checkdams: Odd Structures in CPM Logic Flow

In logic-driven project schedules, the scheduled start and finish of each activity is determined by a “driving path” of predecessor activities and relationships. Driving logic is said to “flow” along this path from the earliest predecessor to the activity’s completion. In simply-modeled projects, this driving logic flow is one-directional and continuous, such that any delay (or acceleration) of a predecessor task is directly translated to a corresponding delay (or acceleration) of its ultimately driven successors. Thus, delaying a task on the “Critical Path” (the driving path to project completion) ultimately delays the project. More complex schedule models – i.e. those using other than finish-to-start relationship links – allow the driving logic flow to be checked or even reversed, so delay or acceleration of a given task may not have the anticipated result on other tasks or on the project as a whole. Such effects can be transient, appearing and disappearing in the course of a single progress update.

Some Cases

Last year I read a series of articles by Miklos Hajdu (Research Fellow at Budapest University of Technology and Economics) on the sometimes-unexpected consequences of certain relationships in logic-driven project schedules. I encountered them again a few months ago during an extended Linked-In discussion that Hajdu started relating to Drag calculation. (BPC Logic Filter is one of the few scheduling tools that actually sets out to compute drag, and we identified some areas needing standardization of definitions.)

Hajdu’s Articles laid out five basic cases where incrementally delaying or accelerating a particular Critical Path activity might not lead to the expected delay or acceleration of the overall project:

Normal Critical Activities (Expected Behavior – i.e. Lengthening task extends project; Shortening task shortens project.)
Neutral Critical Activities (Neither lengthening nor shortening the task has any impact on project completion.)
Bi-Critical Activities (Either lengthening or shortening the task always extends the project.)
Reverse Critical Activities (Lengthening the task shortens the project; Shortening the task extends the project.)
Increasing Neutral Decreasing Reverse Critical Activities (Lengthening the task has no impact on project completion; Shortening the task extends the project.)
Increasing Normal Decreasing Neutral Critical Activities ( Lengthening the task extends the project; Shortening the task has no impact.)

A more recent blog by consultant Pat Weaver, Critical confusion – when activities on the critical path don’t compute…… reviewed these cases and illustrated the consequences using time-scaled-logic diagrams rather than the simple fragnet blocks first used by Hajdu. With graphical images especially, Weaver has done a great job of clarifying the underlying logic flow and emphasizing the consequences of careless planning. His article is a good read. Unfortunately, his suggestion that competent planners should avoid creating any such constructs in their project schedules seems impractical for planners using P6 or Microsoft Project to schedule complex projects.

I had encountered all of these issues previously in various project schedules and and had focused on them quite a bit while developing the drag-associated parts of BPC Logic Filter – that’s where the “Negative, Positive, and Absolute” terminology below came from.

Driving Logic Flow of the Cases

At the start of a project (i.e. ignoring progress updates and Data Date), every activity is scheduled to be completed according to a path of driving logic (comprising predecessor activities AND relationships) extending from the project start milestone or some valid external constraint forward to the activity’s Finish. (For the particular case of the Project Completion activity, its driving path is synonymous with the “Critical Path” of the project.)

Identifying the “Driving Logic Flow” through any arbitrary activity along that path starts with the Relationship Free Float values of its predecessor and successor links. A Relationship Free Float value of 0 indicates a driving relationship, while a value greater than zero indicates a non-driving relationship.
The activity’s duration “participates” in the driving logic flow if (and only if) there are “Driven” and “Driving” relationships at opposite ends of the activity. Various combinations of relationship float have the implications in the table below.

Relationship Float and Driving Logic Flow

Keeping in mind that any changes to activity duration can immediately change the driving logic flow through the schedule and the associated relationship floats – such that an activity described by the first line of the table above may jump to the third line simply by adding a day to its duration – we can interpret the table as follows:

An activity with a Driven Start and a Driving Finish has a Positive duration participation, as the logic flows forward through the duration from Start to Finish. This is “Normal” in Hajdu’s articles; lengthening the task extends the project, while shortening the task shortens the project. This case seems to represent the vast majority of activities in typical schedules. BPC Logic Filter computes a drag value corresponding to the activity duration, any applicable constraints, and parallel (i.e. near-critical) paths.
Positive Duration Participation in Logic Flow (“Normal Critical”)
An activity with a Driven Finish and a Driving Start, on the other hand, has a Negative duration participation, as the logic flows backward through the duration from Finish to Start. This corresponds to Hajdu’s “Reverse-Critical” case; lengthening the task and thereby allowing it to start sooner ends up shortening the project, while shortening the task and thereby forcing it to start later ends up extending the project. BPC Logic Filter computes a negative drag value for these cases, partly to indicate the apparently perverse logic at work. While such tasks seem to be rare in baseline schedules, I have seen them arise during updating on fairly high-level integrated masters (i.e. not in construction).
Negative/Backward Driving Logic Flow through Duration – Starting Early and working slower Helps; Starting Later and working fast hurts.
For an activity with only a Driven Finish and Driving Finish (or Driven Start and Driving Start), then the duration is bypassed and has no participation in the driving logic flow. This corresponds to Hajdu’s “Neutral Critical” case; neither lengthening nor shortening the task has any impact on project completion, and BPC Logic Filter computes a duration drag of zero for task B. It should be noted that although “dangling starts” and “dangling finishes” are evident in the examples depicted below, they are unrelated to the zero-participation observed. Adding non-driving start predecessors and/or finish successors to Activity B would not change the conclusions.
Logic Flow Duration Bypass – Through Finish

Logic Flow Duration Bypass – Through Start
An activity with both driving and driven relationships at both ends (i.e. minimum Relationship Float = 0 in all four columns of the table) represents four parallel driving logic paths: 1) through the Start only; 2) through the Finish only; 3) forward through the Start, the Duration, and the Finish; and 4) backward through the Finish, the Duration, and the Start. In this case, the Duration Participation is “Absolute,” since any change to the activity duration (either positive or negative) results in positive (lengthening) of the overall path. There is no chance to accelerate the project here, so BPC Logic Filter computes a duration drag of 0. This case corresponds to Hajdu’s “Bi-Critical” case. I’ve added an additional predecessor and successor to the illustration fragnets below – mainly to indicate that its occurrence is not limited to ladder-logic structures. The combined “Positive” and “Negative” behaviors are obvious.
Absolute Participation = Positive/Normal on Lengthening, Negative/Reverse on Shortening
Finally, the four variations of “Limited” Duration Participation arise from the cases where three of the four “Relationship Float” columns are zero. They essentially represent various combinations of “Positive,” “Negative,” and “None” cases above, and they correspond to Hajdu’s “Increasing Normal Decreasing Neutral” and “Increasing Neutral Decreasing Reverse” cases. With any of these cases, it is only possible to Lengthen, never to Shorten, the overall length of the project by modifying the duration of Task B, so BPC Logic Filter computes a drag of zero.
Positive Limited Low Participation – Acceleration won’t help, but slippage will hurt.

Positive Limited Low Participation – Acceleration won’t help, but slippage will hurt.

Negative Limited High Participation – Starting early and working longer won’t help, but delaying start will hurt.

Negative Limited High Participation – Starting on-time and working slower won’t hurt, but starting later and working faster will hurt.

Logic Flow Conclusions

Ultimately, these types of odd logic structures seem to arise from two contributory causes:

The legitimate need for project planners to include in the project schedule no more detail than is necessary to plan and control the work (at the level reflected in the schedule). In Primavera P6 and Microsoft Project scheduling software – based on the precedence diagramming version of the critical path method (i.e. PDM/CPM) – this need is partly satisfied by consolidating many single activities representing simple tasks (with only Finish-to-Start relationships) into longer activities representing more complex work, connected with relationships other than Finish-to-Start. Common examples are Finish-to-Finish and Start-to-Start, often with time or volume lags. As a consequence, driving (controlling) predecessor logic can either “push” an activity (through its “Driven Start”) OR “pull” the activity (by its “Driven Finish”) – or both. Similarly, the activity may drive its logical successors through its “Driving Start” or its “Driving Finish.”
The continuous-activity assumption in the prevailing PDM software packages like P6 and MSP. That is, while the activity may be pushed and/or pulled by predecessor logic, the activity’s duration remains as a rigid connection from Start to Finish, neither stretching nor compressing (nor splitting into parts) in response to logical pressures alone. Consequently, the activity’s duration will be scheduled at the earliest continuous interval that satisfies the most stringent of its start/finish predecessor relationships. All other predecessor relationships will possess “relationship free float.”

Within P6 and MSP schedule models, using Ladder Logic to approximate progressive feeding of work volumes between largely parallel activities is a technique that effectively models the actual work interfaces. Yet it seems virtually guaranteed for such paired-activity ladder structures to encounter at least “neutral-critical” and sometimes “bi-critical” driving logic flow during updating. In my opinion this should be acceptable as long as the paired activities are effectively managed together.

Negative (“Reverse-Critical”) driving logic flow, however, reflects a case where the work being depicted is too complex to be represented by a single activity, and further breakdown is needed. Since it also provides an opportunity for the scheduler to sequester or otherwise manipulate float, the underlying logic structure may be indirectly prohibited by scheduling specifications. BPC Logic Filter presently flags reverse flows of driving logic (using negative drag) during the drag analysis.

The multiple cases where the driving logic flow effectively bypasses an activity’s duration (“Neutral-Critical”) appear to be a natural outcome of the scheduler’s intent. In addition, they seem consistent with the actual work interfaces in some construction projects, particularly where there are substantial variations in the production rates of parallel activities. While BPC Logic Filter doesn’t currently identify such cases, it seems reasonable to modify the Gantt-bar coloring routines in a future release.

Ladder Logic (Parallel SS/FF Relationships) in Microsoft Project

Microsoft Project does not allow users to create multiple logical relationships between the same two tasks. Project DOES ALLOW importing of such multiple relationships in XML files, however. If desired, users can directly edit XML versions of project schedules to introduce multiple logical relationships, and these relationships appear to be persistent and active in all subsequent schedule calculations.

Microsoft Project and Oracle’s Primavera P6 are the two dominant tools for complex project scheduling in North America, and I’ve been a regular user of both tools and their predecessors since the early 1990s. Aside from major issues related to data architecture, one of the key remaining differentiators from a user’s point of view is Project’s limit of one logical relationship between any two pairs of activities.

This limit can be a deal-breaker for longtime users of other tools who are dependent on scheduling workflows using “ladder logic”, or concurrent SS/FF relationships with lag. This kind of logic is used to represent sequentially-related activities whose overall characteristics allow them to proceed mostly in parallel. In construction, a simple example might include digging 1,000 meters of trench, laying 1,000 meters of pipe in the trench, and covering the trench. The most timely and profitable approach to the work is to execute the three tasks in parallel while providing adequate work space between the three crews whose production rates are well matched. Using ladder logic, it is possible to model the work using three relatively long duration activities with concurrent SS and FF relationships. Appropriate time lags are assigned to the relationships to represent the necessary space (or work volume) offsets between the activities. A similar approach can be used to schedule shorter-duration activities performed by successive crews at the same location, where availability of ready work front for the follow-on crew is the the primary constraint. [See also: Overlapping Tasks in Project Schedules.]

In my own experience, I’ve found ladder logic useful for effectively modeling the field approach while avoiding unnecessary detail in the schedule. Implementing ladder logic in Microsoft Project (MSP) requires the use of dummy milestones, complicating the logic and adding needless detail. I would prefer to avoid this workaround. Recently I learned that the one-relationship limit may not be irrevocable, and combined SS/FF links may be used to implement pure ladder logic in MSP (with some outside help.)

Figure 1 illustrates a simple fragnet (in P6) comprising three activities that are linked together with ladder logic. (This is just a test schedule; the implied work relationships are meaningless.)

Figure 1: Typical Ladder Logic in P6 — Figure 1: Typical P6 Ladder Logic with Concurrent SS/FF Relationships and Lags

Figure 2 illustrates the same fragnet (this time in MSP Pro 2010). Dummy milestones have been added to carry the logic through the Start-to-Start side of the ladder, so five activities are needed to schedule the same work that requires only three in P6.

Figure 2: Typical MSP Ladder Logic Using (Dummy) Milestones

Figure 3 demonstrates a fully-functioning MSP fragnet that incorporates dual SS/FF relationships without the aid of dummy milestones. The relationships appear to be fully functioning in the forward-pass and backward-pass calculations, and they are fully editable.* (Like all relationships in MSP, changing the predecessor or successor task requires deletion and re-initiation of the relationship, i.e. not an edit.) It appears, therefore, that multiple relationships between a single pair of tasks does not automatically break the schedule calculations in MSP Pro 2010. Unfortunately, the only way I’ve found to add these relationships is by directly inserting them into an xml version of the schedule file, then opening the file with MSP. (Similarly, P6 schedules that are transferred to MSP through the xml interface can manage to keep their redundant links.) Once opened, MSP appears indifferent to the presence of these externally-inserted dual relationships, but it continues to prohibit introduction of new ones, whether through the standard user interface or through direct manipulation of the underlying data in the open project.

*Interestingly, the only way to successfully edit the dual relationships is using the predecessors or successors list in one of the “task form” lower-pane views as shown here. Attempting to edit using the Predecessors tab of the Task Information dialog window or using the predecessors or successors column in a task table fails — with MSP deleting rather than editing the relationship.

Figure 3: Ladder Logic Loaded Through Edited XML File — Figure 3: Ladder Logic w/ Concurrent Links Loaded Through XML

Overall, I’m encouraged that Project’s longstanding limitation of one relationship per pair of tasks is not – apparently – an inevitable and unavoidable consequence of the program design. Nevertheless, inserting redundant relationships through xml editing hardly seems workable in general, and I doubt that I’ll be using this technique much going forward.

Find the Connections Between Two Arbitrary Tasks in a CPM Schedule

BPC Logic Filter includes a little feature called Bounded Network (Target Task) Analysis. The feature allows a user to identify all the logical path(s) connecting two arbitrary tasks (or connecting a group of tasks to a single task) in a Microsoft Project schedule. I wrote a few (very dry) pages on it beginning around page 6 of the documentation: Introduction to BPC Logic Filter

I developed this feature out of my own need to efficiently communicate task dependencies to project stakeholders. For example, a piece of major equipment is scheduled to arrive on-site (pre-assembled) on 1April, but it is not scheduled for handover until 1July. For the eventual equipment owner, it is useful to have a graphical depiction of all the tasks – and only those tasks – leading from arrival to handover during the intervening three months (e.g. setting in place, hookups, mechanical inspection, systems testing, commissioning, acceptance testing, endurance testing, training, etc.) While sometimes such tasks all share a common WBS code or custom field, it is rare that such codes correspond 100% with the logical chain(s) of required activities. A logic-based filter provides a clearer picture.

Within the last few days I participated in a LinkedIn discussion on how to develop a similar filter in Primavera (i.e. Oracle Primavera P6), and I’m embarrassed to admit that my initial suggestions (to use Multiple Float Path) were completely wrong. In fact, the quickest way to show the connections between two arbitrary activities is to create a logical loop between them, then try to reschedule the project. P6’s error handler will list all the connecting tasks.

P6 won’t generate the logical filter for you, but the user interface has a very handy feature of being able to add activities to a pre-existing view by simply clicking on the “Goto” buttons in the relationship windows. The list generated by the loop error will guide your selections.

Here’s an example, taken from a ~2000-activity schedule for an ongoing marine project. I have selected two activities whose relationship is not obvious, but which are indeed related.

Figure 1: Filter for 2 Arbitrary Connected Activities

(Using Multiple Float Path analysis of the electrical activity “Connect Paceco…,” I found the plumbing activity “New 4 PW….” activity on float path 168. I didn’t count the activities in float paths 2 through 167, but we need to exclude most of them without examination. MFP is clearly not the answer.)

As shown on Figure 1, I first add a circular successor relationship from the later activity, “Connect Paceco…” to its distant predecessor, “New 4 PW….) Then I try to re-schedule the project. If no error is generated, the two tasks are not related, or the predecessor/successor direction of the connections may be the opposite of what you expect. Figure 2 shows the expected error message, with the listing of the looping paths.

Figure 2: P6 Circular Logic Message (with my cheats)

Now use the list as a guide to attach the connected activities to the existing view.

The result after completing the loop:

Figure 4: Manually Constructed Filter of Path Connecting 2 Arbitrary Activities

You might be tempted to make this into a permanent filter by assigning some custom coding to the visible activities and then making the corresponding filter specification. That doesn’t seem to be worth the extra time to me unless I know for sure that I will be using this filter again. A pdf or screen shot may be all I need.

Many thanks to Khuong Do for raising this question in the Primavera group on LinkedIn. In addition, while the method of manually constructing logical filters by jumping through relationships has been around for many years, I thank Zoltan Palffy and Gail Adams for reminding me that it is still there in P6. Using the circular logic report is something I would never have thought of on my own. All credit to Mr. Gerry Smith in the Primavera LinkedIn group for that stroke of genius.

Just for comparison, I used a laborious process to export this project from P6 to Microsoft Project so that I could run the similar report from BPC Logic Filter. Here’s the result. Yellow and Orange highlighters identify the “Selected” and “Target” tasks respectively. (The P6-to-MSP export/import process is crude: Activity IDs were lost. Calendars were lost, so dates were corrupted. Logic came through with no problems, however.)

Figure 5: Target Task Output from BPC Logic Filter

Beyond the Critical Path – the Need for Logic Analysis of Project Schedules

This entry is intended to review the use of the Multiple Float-Path calculation option in Primavera Project Management (P6) and to offer a brief example of its use compared to BPC Logic Filter (for Microsoft Project).

Project schedules generated using the Critical Path Method (CPM) are commonly used to model – and to document – the project team’s plan for executing the scope of work. Such a plan normally involves identifying necessary activities at an appropriate level of detail and specifying the necessary sequential relationships between them. The output from the CPM analysis is a list of activities with associated durations, dates, and float values – this constitutes “the schedule”.

Unfortunately, the sequential relationships that ultimately drive the schedule (i.e. the logical “plan”) can be difficult to communicate or analyze for all but the simplest projects. This is because Total Float – the telltale indicator of logical-path connectivity in simple projects – becomes unreliable (or unintelligible) for such purposes in the presence of variable activity calendars or late constraints. As a result, complex schedule models lose both usefulness and credibility among project stakeholders unless schedule managers go beyond the simple communication of dates, durations, and float.

Multiple Float Paths

Oracle’s Primavera P6 software (P6) has always included an option to compute “Multiple Float Paths” when calculating the schedule, but many experienced planners seem unfamiliar with it. The option facilitates the identification of the “driving” and “near-driving” logical paths for a single selected activity. The selected activity can be a key project milestone that may or may not correspond to the end of the project, or it may be a simple intermediate activity of particular or urgent concern.

Figure 1 represents a simple project for construction and handover of a small utility installation – originally modeled in Microsoft Project and then converted to Primavera P6. (The model was developed primarily for illustrating the impact of calendars and constraints; the work techniques illustrated are neither typical nor ideal.)

There are contractually-derived late-finish constraints on the Construction Project Complete milestone (24Apr’15) and the final Project Acceptance milestone (29Apr’15). These constraints affect the late dates (and consequently Total Float) for these activities and (parts of) their chains of predecessors.
There is a late-finish constraint (25Feb’15) on the “Install Fence” activity (reason not known), with similar impacts on late dates and Total Float.
Activities are scheduled using a 4d x 8h work week (M-Th), except for the two initial milestones which utilize a 24-hour calendar, and the final two Customer Checkout activies which utilize a 5d x 8h workweek.
The “Notice to Proceed” milestone is constrained to start no earlier than 10:00 PM on 05Jan’15.
P6’s scheduling options are set to define critical path activities on the basis of “Longest Path” rather than Total Float, and the Gantt chart appears to properly display the Critical Path by this definition. Thus, the two initial milestones are marked as critical because they are driving the project’s completion, even though their calendars allow a higher value for total float.

Figure 1: (P6) Simple Construction/Handover Project

Although “Longest Path” appears to correctly identify the driving path to the project completion (the Project Acceptance milestone), the contractor is equally interested in identifying the driving path to the “Construction Project Complete” intermediate milestone.

In P6’s advanced schedule options, we select “calculate multiple float paths” ending with the “Construction Project Complete” milestone” (Figure 2). As a rule, we calculate the multiple paths using “free float” rather than “total float”, since the former option best mimics “longest path” behavior.* The default number of paths to calculate is ten.

* See “P6-multiple-float-path-analysis-total-float-and-free-float-options” for more on these options.

Figure 2: (P6) Schedule Option for Multiple Float Paths

Figure 3 illustrates the result of re-calculating the schedule then displaying a layout that arranges the activities by “Float Path” and sorting by “Float Path Order”. In this figure, “Float Path 1” is the driving logical path leading to the Construction Project Complete milestone. “Float Path 2” defines the first near-driving-path, “Float Path 3” defines the next near-driving path, etc. Each “float path” is essentially a discrete branch from the main, driving logical path. Obviously, Float Path 1 defines the activities that offer the most opportunity to accelerate the construction project (and maybe the most risk of extending it.) According to the figure, higher float paths tend to have higher values of total float, though the correlation is not universal.

Figure 3: (P6) Multiple Float Paths to Interim Milestone

Unfortunately, P6 does not rigidly distinguish between driving-paths and near-driving paths. That is, while float path 1 is always “the” driving path, float path 2 may designate another, parallel driving path or a path that is 2 days from the driving path. It is not obvious how far a certain numbered path may be from driving; that is, what is its “relative float” with respect to the end activity? You can try to estimate this manually by looking at start and finish dates of various related activities in the output. More rigorously, the relative float of each path can be computed by summing the “Relationship Free Float” of all the relationships between the given path and the end activity. [Jul’18 Edit: In certain cases P6’s path-selection criteria can relegate parallel driving-path activities – even Longest-Path activities – to high-numbered float paths that appear far from the driving path. I described this in a later article – Relationship Free Float and Float Paths in Multi-Calendar Projects (P6 MFP Free Float Option).]

Ongoing management of projects often requires what-if analysis of prospective disruptions, and P6’s MFP can be useful. For example, the subcontractor for the “Install Bus and Jumpers” activity may request early access to accommodate a staffing conflict. Running MFP ending with “Install Bus and Jumpers” will identify the driving path of predecessors for this work (Figure 4), assisting in the review and consideration of the request.

Blog151226Fig4 — Figure 4: (P6) Multiple Float Path to Install Bus and Jumpers

Figure 4 demonstrates the utter lack of correlation between Total Float and the driving logical path for any given activity in the schedule.

A Word about LOE Activities and ALAP Constraints (P6)

Depending on the scheduled dates, P6 automatically sets the relationships of LOE (level-of-effort) activities to “Driving”. As a consequence, P6’s Longest Path algorithm traces driving flags directly through LOE activities to their non-critical predecessors, and these end up – incorrectly – on the Longest Path. Fortunately, this error seems to be avoided in Multiple-Float Path analysis. MFP tracing correctly identifies only true driving logic and excludes LOE activities from the trace. (I’ve illustrated this in another entry HERE.)

Like LOEs, predecessor relationships from activities with ALAP (as-late-as-possible) constraints in P6 can be flagged as “Driving” based on their dates alone. Consequently, each ALAP-constrained predecessor creates a new parallel driving path to the selected end activity, and these paths are mapped in the MFP analysis. Since ALAP-constrained activities are rarely actually driving anything, it can be useful to filter them out from standard MFP layouts.

Multiple Float Path Analysis in Microsoft Project

(Microsoft Project provides neither Longest-Path nor Multiple-Float-Path analysis. BPC Logic Filter is an add-in that applies similar calculations to MSP schedules.) Figure 5, Figure 6, and Figure 7 illustrate the same steps as above, but this time executed on the Microsoft Project version of the schedule using BPC Logic Filter. In this type of analysis, the primary difference between P6 and BPC Logic Filter is that BPC Logic Filter explicitly computes and displays “Relative Float” (i.e. days away from driving) for each path. Thus two logical paths with the same relative float (i.e. parallel paths) are grouped together in BPC Logic Filter, while P6 assigns separate float paths. The MSP add-in also re-colors Gantt bars based on their path relative float with respect to the “selected” task.

Figure 5: (MSP) Simple Construction/Handover Project

Figure 6: (MSP) BPC Logic Filter – Multiple Float Paths to Interim Milestone

Figure 7: (MSP) BPC Logic Filter – Driving Path to Install Bus and Jumpers

Finally, BPC Logic Filter allows a more substantial evaluation of the upstream and downstream logic affected by the potential change to “Install Bus and Jumpers”. Figure 8 identifies the predecessor and successor paths for the selected task, all arranged according to their path relative float (shown at the end of each bar) with respect to the selected task. This illustrates that, while the selected work cannot be accelerated without violating (or modifying) its driving predecessor logic, it may be delayed by up to 12 days without affecting any successor work.

Figure 8: (MSP) BPC Logic Filter – Driving and Driven Paths for Intermediate Activity (Install Bus and Jumpers)

As a long-time Primavera user accustomed to MFP analysis options, I was continually disappointed when faced with the need for logical path analysis in Microsoft Project. I wrote BPC Logic Filter in part to cover this gap; now I find myself facing disappointment in the opposite direction.