In Project schedules, the Longest Path yields the Shortest Time. Aside from the mental gymnastics needed to digest that phrase, the concept of Longest Path – especially as implemented in current software – has deviated enough from its origins that a different term may be needed.
Critical Path as Longest Path
Authoritative definitions of the “Critical Path” in project schedules typically employ the words “longest path,” “longest chain,” or “longest sequence” of activities … (that determine the earliest completion date of the project.) In other words, the path, chain, or sequence with the greatest measured length is the Critical Path. As a rule, however, none of the associated documents are able to clearly define what constitutes the length of a logic path, nor how such length will be measured and compared in a modern project schedule. Without a clear standard for measuring the length of something, explicitly defining the Critical Path in terms of the longest anything is just sloppy in my view.
The Original Path Length
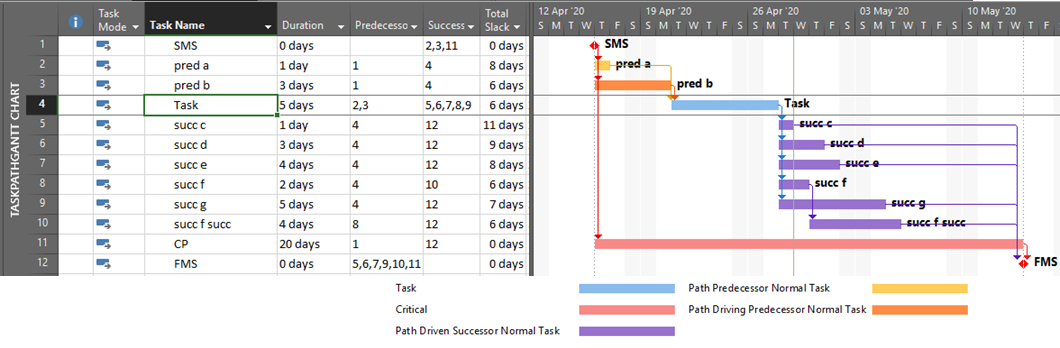
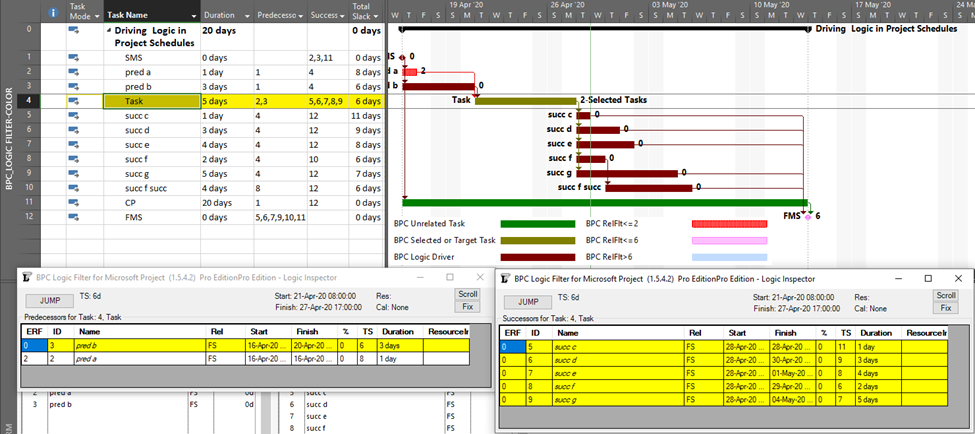
Assessing path length used to be much easier. In the early days of CPM (Critical Path Method) scheduling, any project schedule could be guaranteed to have ALL Finish-to-Start relationships, NO constraints, NO lags or leads, NO calendars, and only ONE Critical Path. Under these conditions, the length of a logic path could be clearly defined (and measured) as the sum of the durations of its member activities. Thus, the overall duration of a Project was equal to the “length” (i.e. duration) of its Critical Path, which itself was made up of the durations of its constituent activities. That result is indicated in the figure below, where the 64-day project length is determined by the durations of the 5 (highlighted) activities on the Critical Path. Adding up the activity durations along any other path in the schedule results in a corresponding path length that is less than 64-days – i.e. not the “longest” path. [The network diagram was taken from John W. Fondahl’s 1961 paper, “A Non-Computer Approach to the Critical Path Method for the Construction Industry,” which introduced what we now call the Precedence Diagramming Method. Unfortunately, Microsoft Project (MSP) has an early limit on dates, so his presumed ~1961 dates could not be matched.]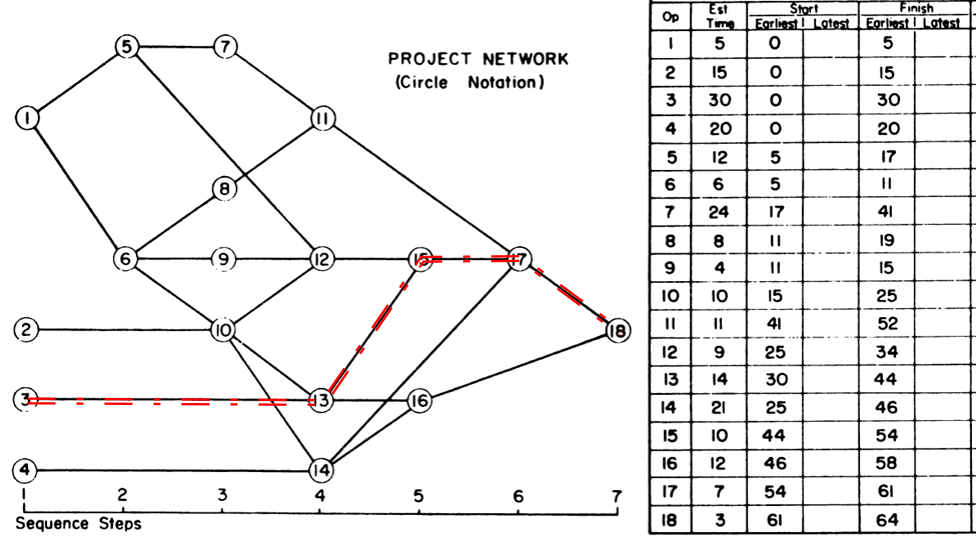
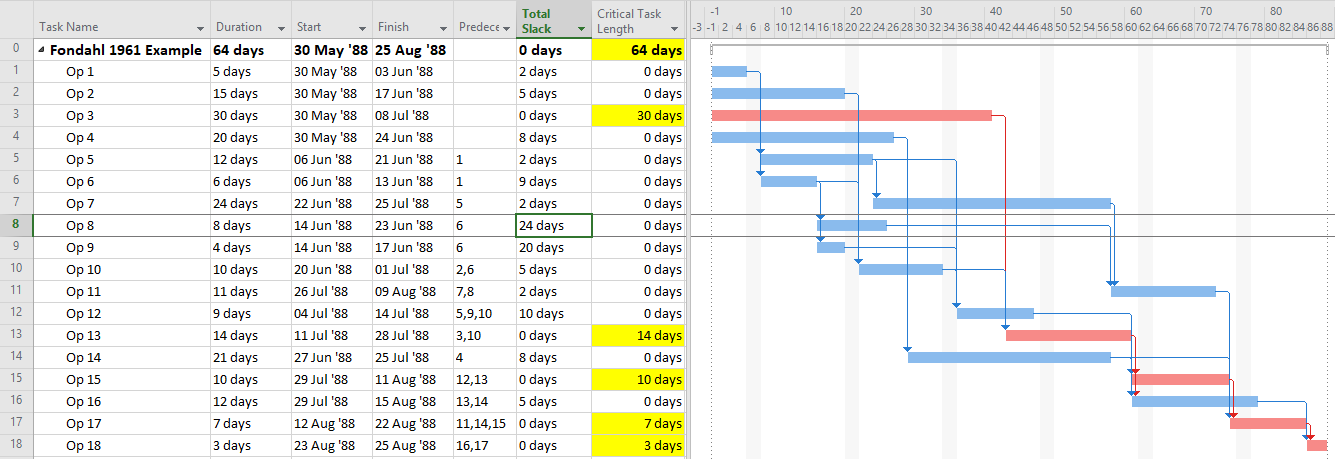
Fortunately, in such simple projects, it’s never been necessary to aggregate and compare the lengths of every logic path to select the “longest path.” The CPM backward pass calculations already identify that path by the activities with zero-Total Float/Slack, and successively “shorter” paths are identified by successively higher Total Float/Slack values. This fact has been verified in countless student exercises involving simple project schedule networks, typically concluding with the axiom that “the Critical Path equals the longest path, which equals the path of zero-Total Float/Slack.”
Float/Slack and Path-Length Difficulties
In general, modern complex project schedules have, or can be expected to have, complicating factors that make Total Float/Slack unreliable as an indicator of the Critical Path – e.g. non-Finish-to-Start relationships, various early and late constraints, multiple calendars, and even resource leveling. See this other article for details. Therefore, as noted earlier, the axiomatic definition has been shortened to “the Critical Path equals the longest path.”
Unfortunately, finding the “longest path” by arithmetically summing the activity lengths (i.e. durations) along all possible logic paths and comparing the results – not easy to begin with – has gotten more difficult. Lags, excess calendar non-working time, and resource leveling delays all add to the apparent “length” of a logic path compared to the simple summation of activity durations. Early date constraints may introduce delays that are not justified by task durations or logic relationships, breaking the path altogether. On the other hand, leads (negative lags), excess calendar working-time, and the use of overlapping-activity relationships (e.g. SS/FF) reduce its length. In addition, any hammocks, level-of-effort, and summary activities need to be excluded. All such factors must be accounted for if the “longest path” is to be established by the implied method of measuring and comparing path lengths in the project schedule. I don’t know of any mainstream project scheduling software that performs that kind of calculation. Alternatively, Deep Schedule AnalysisTM using the proprietary HCP (Hidden Critical Path) Method – from HCP Project Management Consulting – appears to compute and compare the lengths of all logic paths in Primavera and MSP schedules.
Longest Path as Driving Path
Contrary to summing up and comparing logic path lengths, most current notions of the “longest path” are based on an approach that does not involve path “length” at all. As a key attribute, the longest path in a simple, unconstrained and un-progressed project schedule also happens to be the driving logic path from the start of the first project activity to the finish of the last project activity. It is a “driving logic path” because each relationship in the path is “driving”, that is it prevents its successor from being scheduled any earlier than it is. Driving relationships are typically identified during the forward-pass CPM calculations. Subsequently, the driving path to the finish of the last activity can be identified by tracing driving logic backward from that activity, terminating the trace when no driving predecessors are found or the Data Date is reached. The resulting driving path to project finish is sometimes called the “longest path” even though its “length” has not been established. This is the “Longest Path” technique that has been applied for nearly two decades by (Oracle) Primavera and adopted more recently in other project scheduling tools.
As of today, MSP continues to define Critical tasks on the basis of Total Slack, but it provides no explicit method for identifying the “Critical Path” using a “longest path” criterion. How is the responsible MSP scheduler supposed to respond to a demand for the “critical path” when the longest path has been obscured? Here are several options:
- Continue to make simple projects, avoiding all complicating factors like calendars (including resource calendars), early and late constraints, deadlines, and resource leveling. Then assume that “Total Slack = 0” correctly identifies the Critical Path.
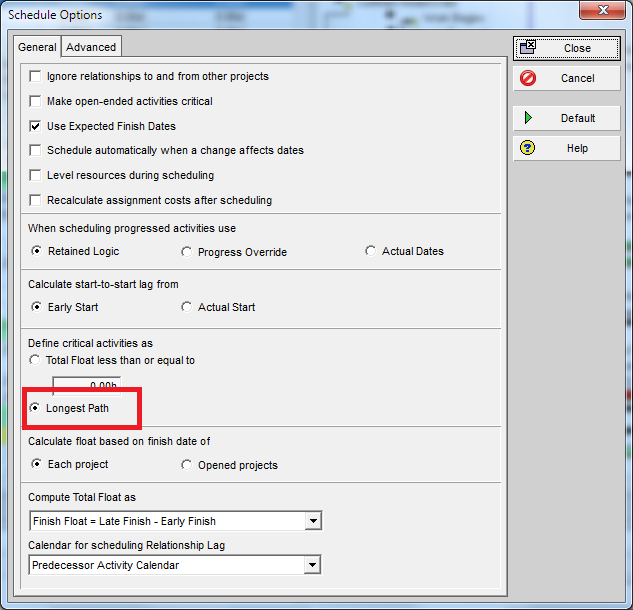
- If you are using MSP version 2013 or later,
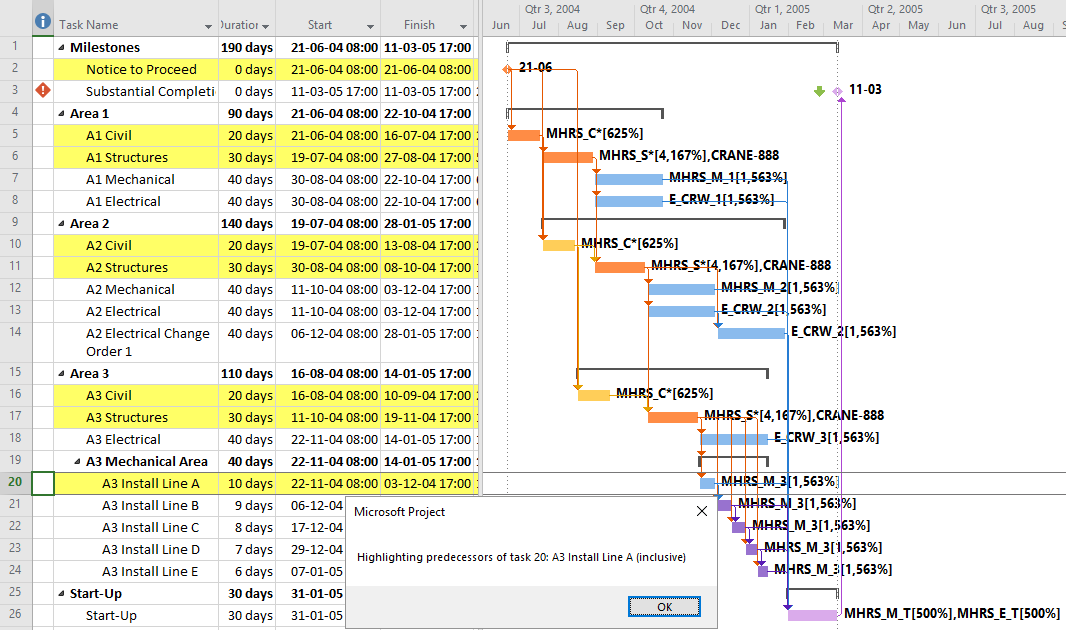
- Ensure that your project is properly scheduled with logic open-ends only present at a single start and single finish task/milestone, then select the single finish task,
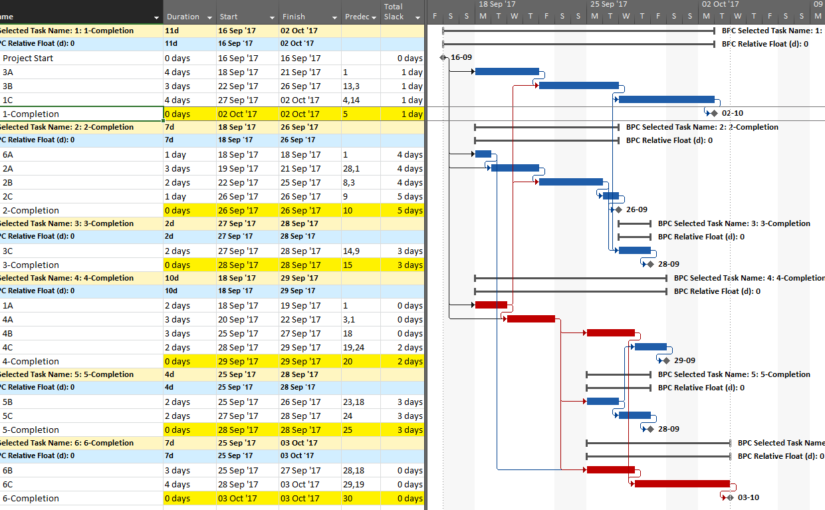
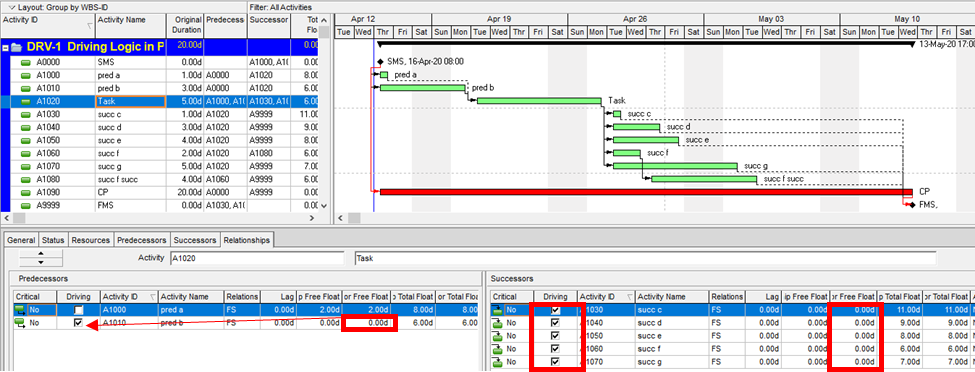
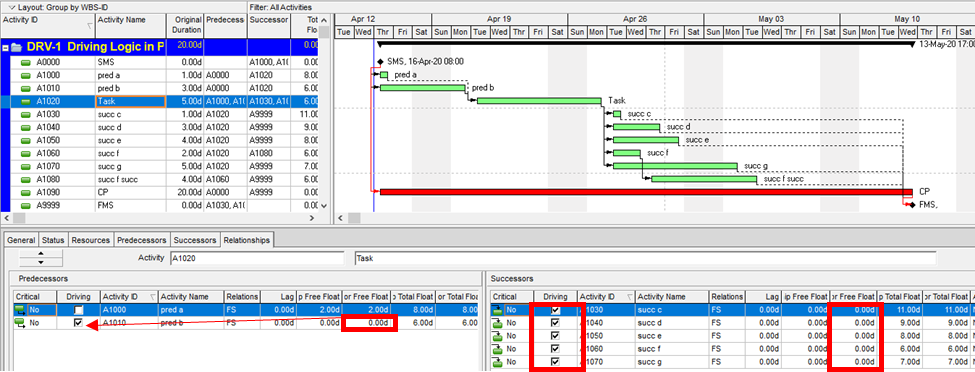
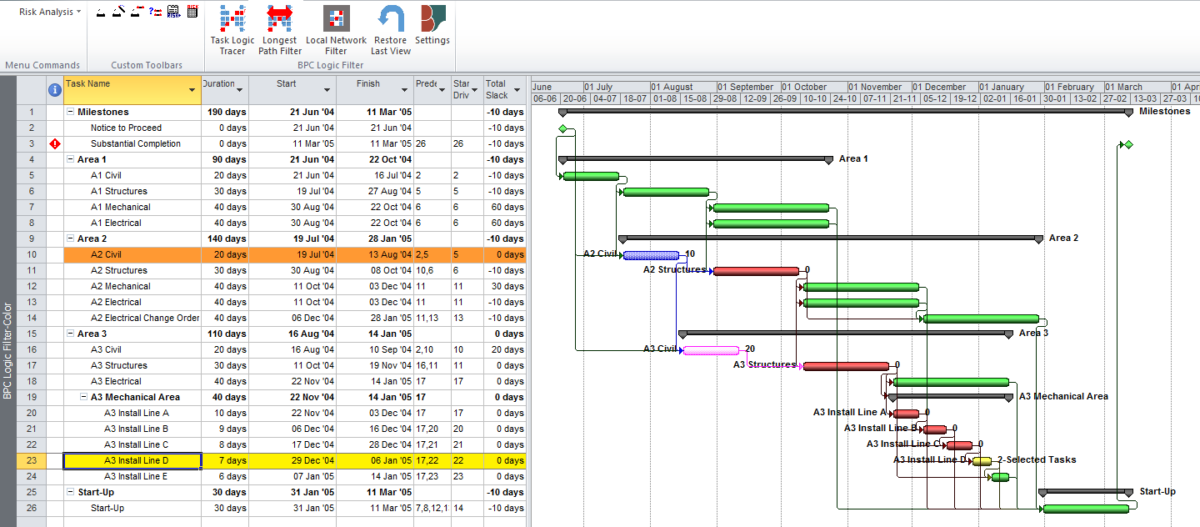
- Try to use the “Task Path” bar highlighter to highlight the “Driving Predecessors” of your selected finish task. In the example below, a Deadline (a non-mandatory late-finish constraint) has been applied to task Op12 in the 1961 example, and MSP has responded by applying the “Critical” flag (based on TS=0) to Op12 and its predecessors Op10 and Op2. As a result, the Critical Path is obscured. Applying the bar highlighter and selecting task Op18 (the project’s finish task) correctly identifies the driving path to project completion, i.e. the “longest path.” (For clarity, I manually added the corresponding cell highlighting in the table; the bar highlighter doesn’t do that.)
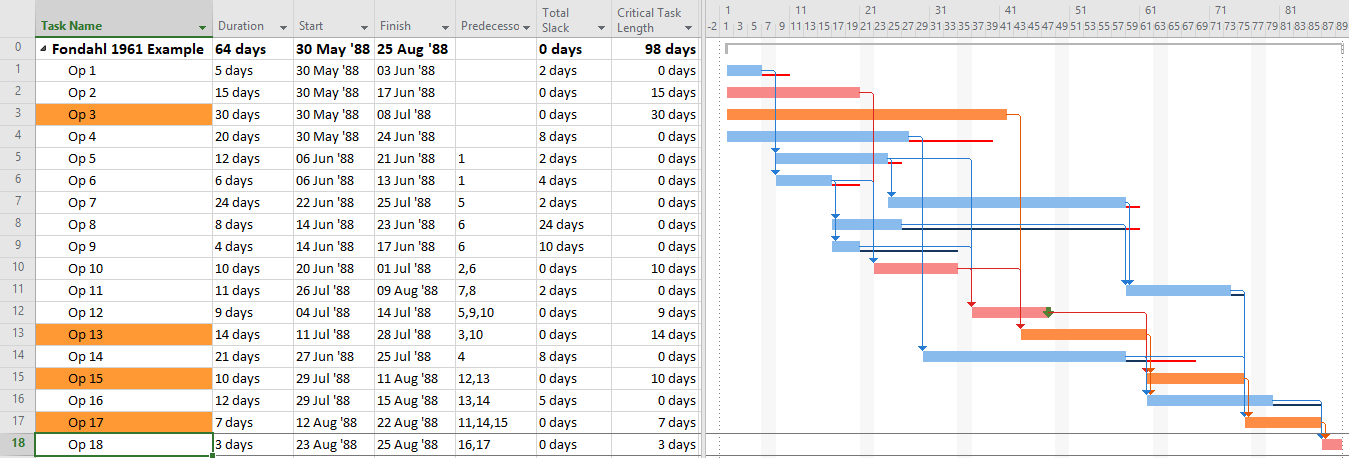
- If necessary, create and apply a corresponding filter for the highlighted bars. I’ve posted a set of macros to make and apply the filter automatically in this article.
- If you are using MSP version 2007 or later,
- Ensure that your project is properly scheduled with logic open-ends only present at a single start and single finish task/milestone, then select the single finish task,
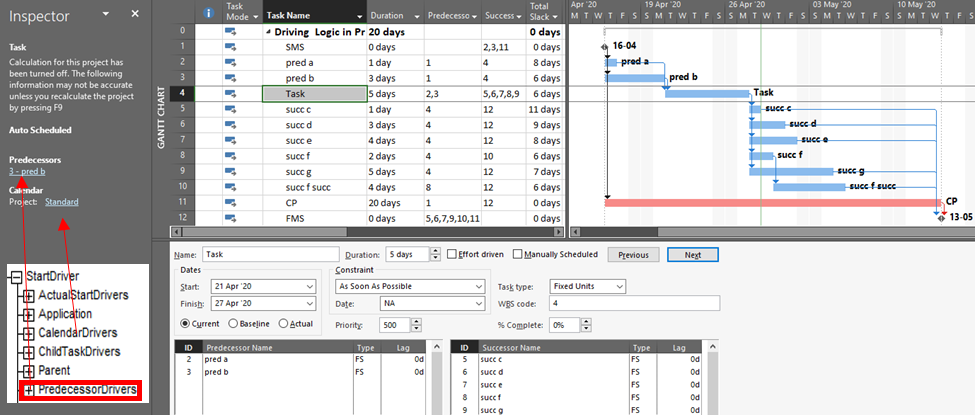
- Try to use the Task Inspector to identify the driving predecessor of the selected task, then go to it and flag it as being part of the driving path. Repeat this until the entire driving path is marked.
- If necessary, create and apply a filter and/or highlighting bar styles for the flagged tasks.
- I’ve posted another set of macros to do all this (except bar highlighting) automatically in this other article.
- Note: The previous two approaches both rely on MSP’s StartDriver task object to identify driving relationships. As noted in this article, however, the resulting driving logic is not reliable in the presence of tasks with multiple predecessors, non-FS predecessors, or actual progress.
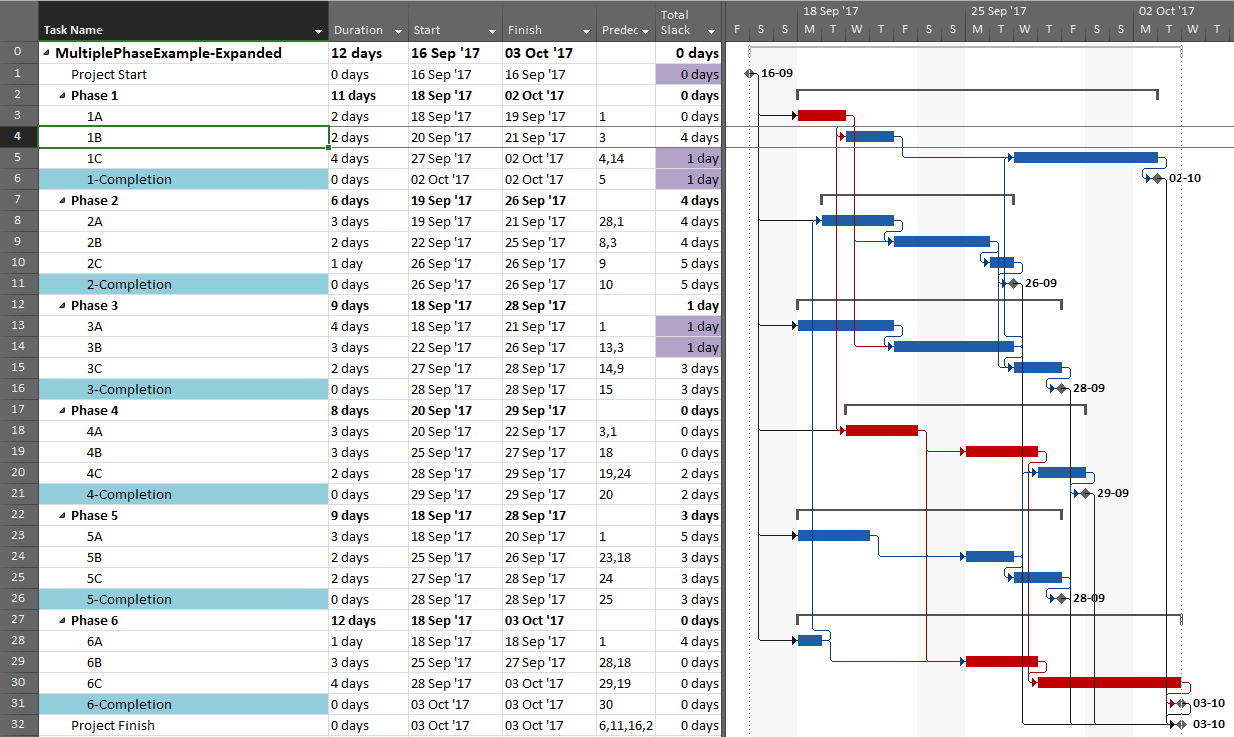
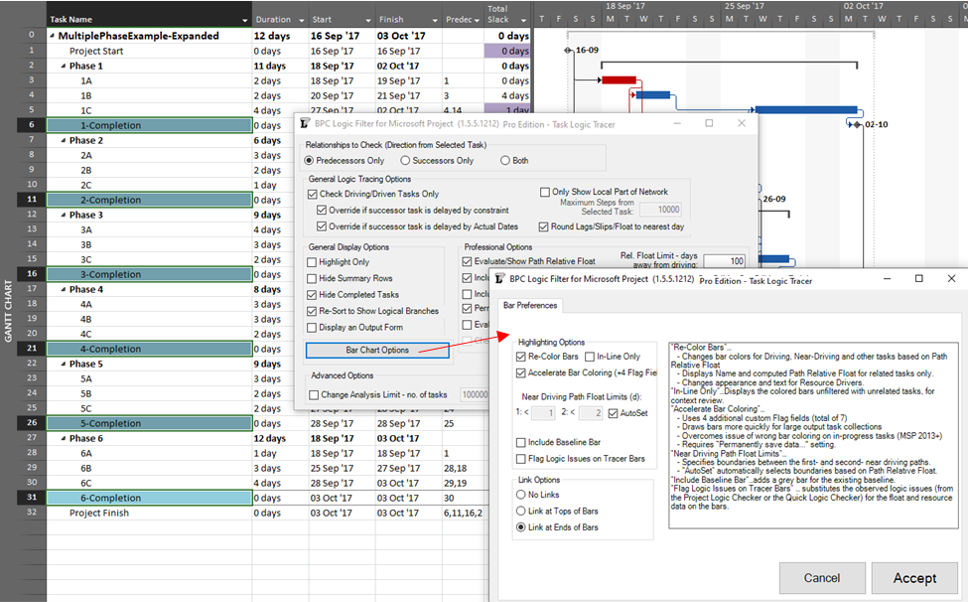
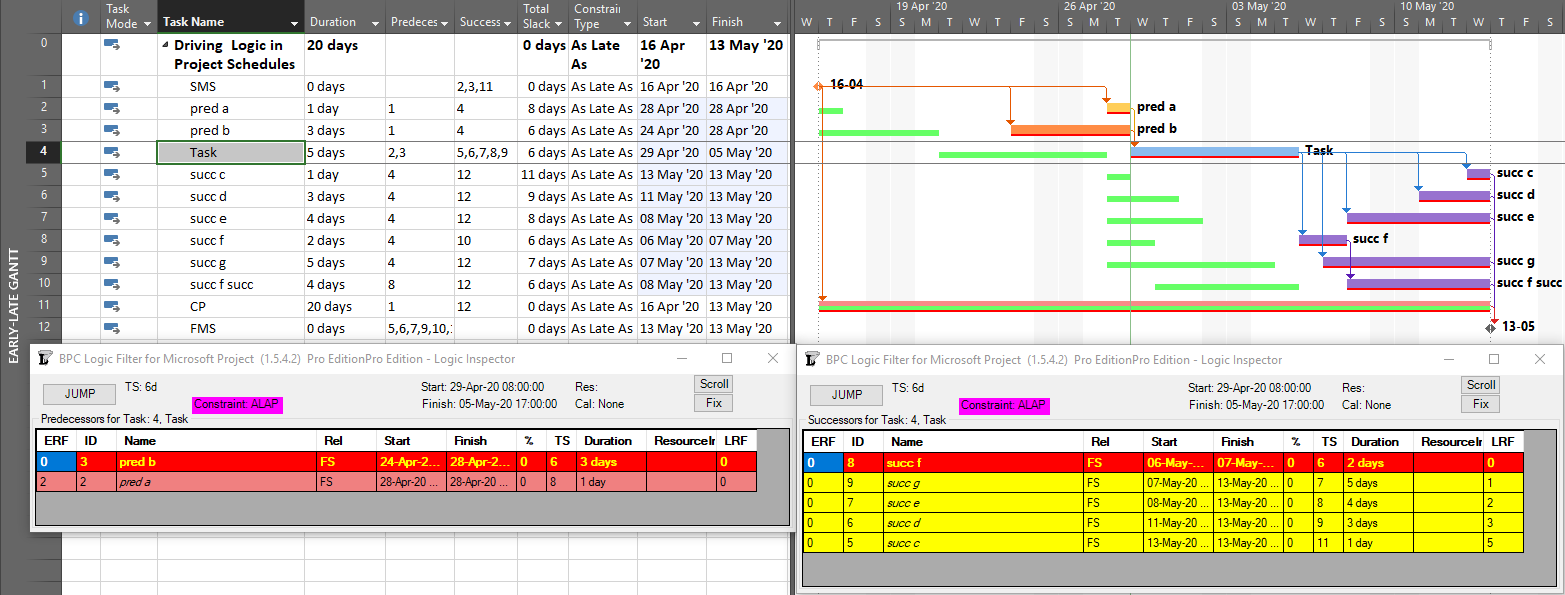
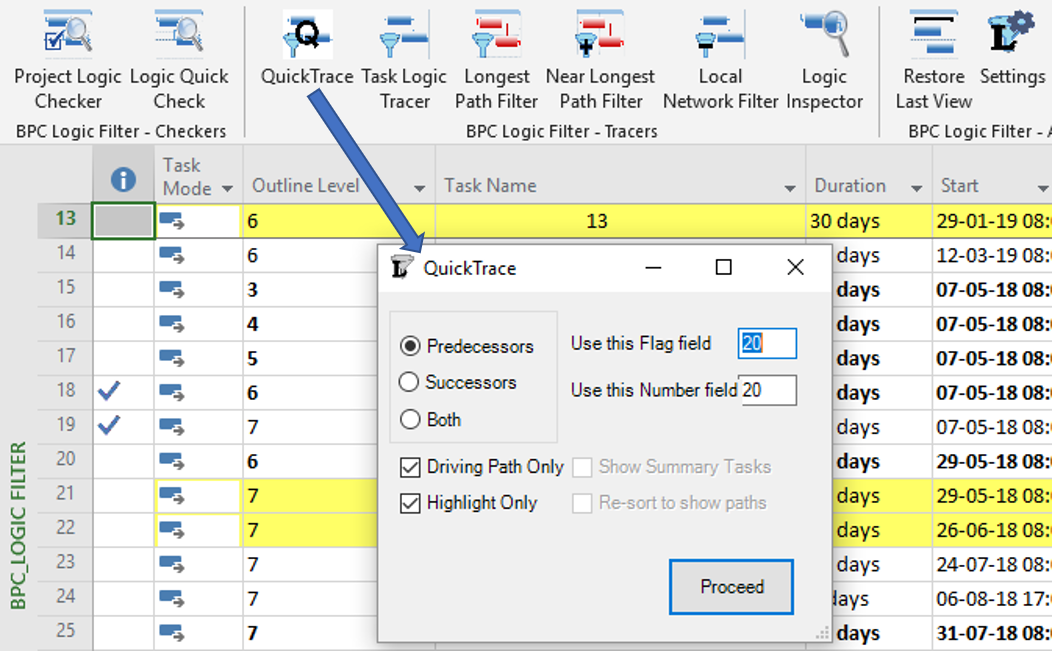
- Use BPC Logic Filter or some other appropriate add-in to identify the “longest path” in the schedule.
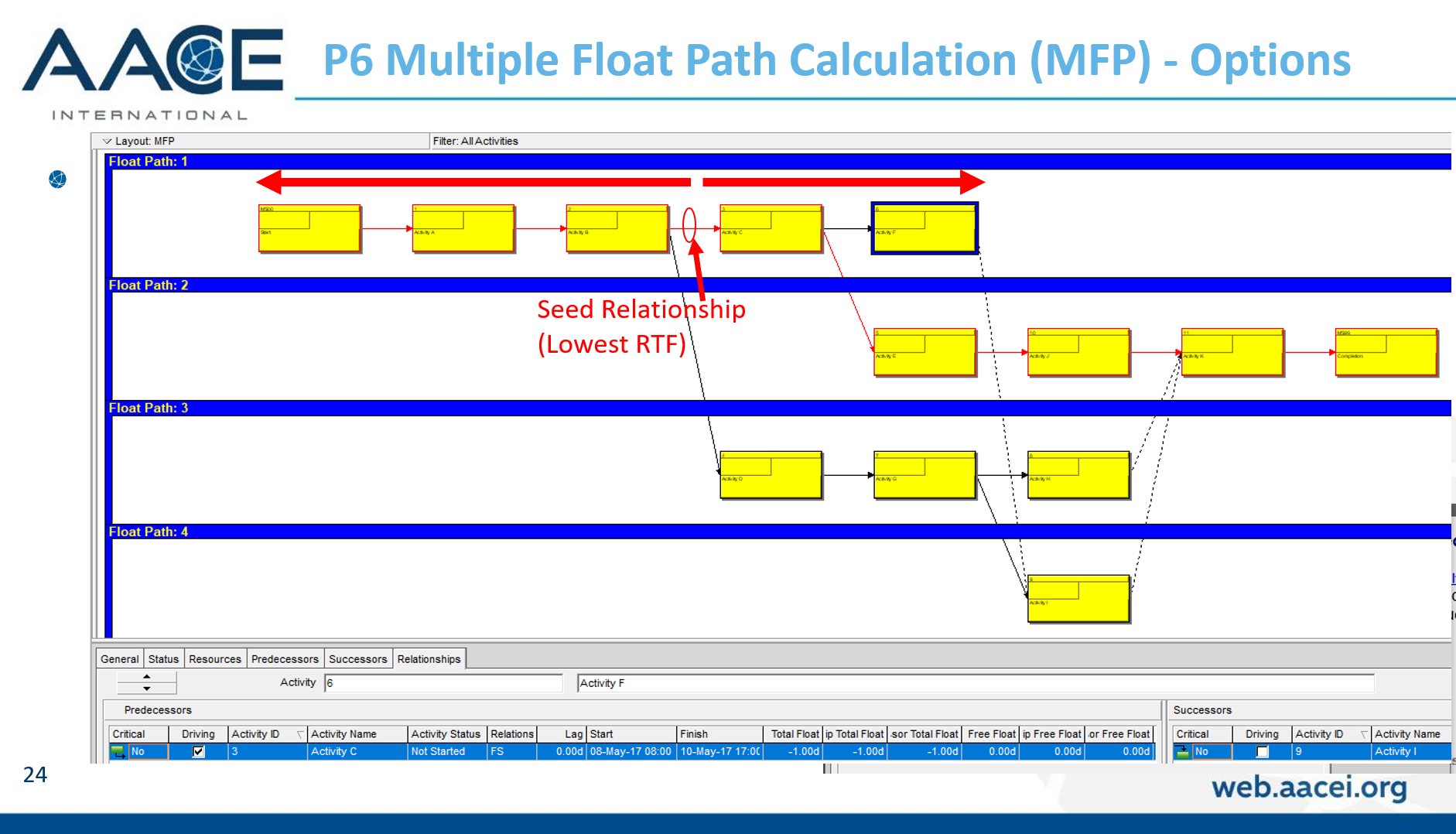
Whichever method or software is used, expressing the Longest Path using the Driving Path methodology has one key weakness: it has not been proved generally useful for analysis of near-critical paths. While the Longest Path may be known, its actual length is not readily apparent. More importantly, there is no generally-accepted basis for computing the lengths, and hence the relative criticality, of the 2nd, 3rd, and 4th etc. Longest Paths. Consequently, Near-Critical paths continue to be identified based on Total Float/Slack, which is still unreliable, or – in P6 – based on unit-less “Float Paths” from multiple float path analysis.
“Longest Path” and Early Constraints
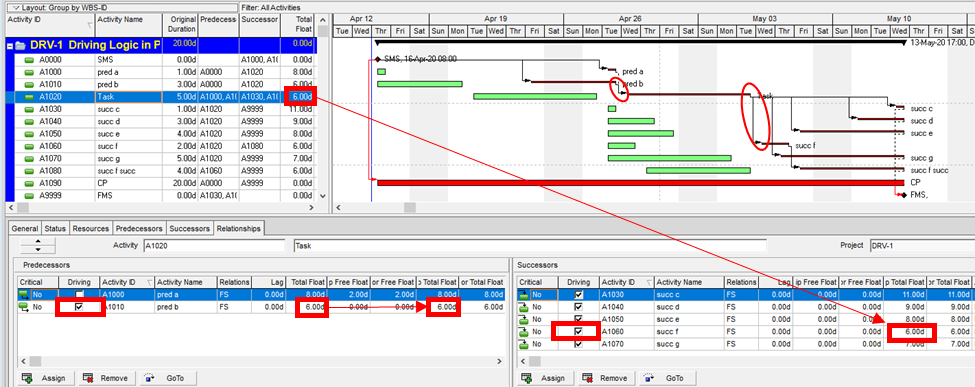
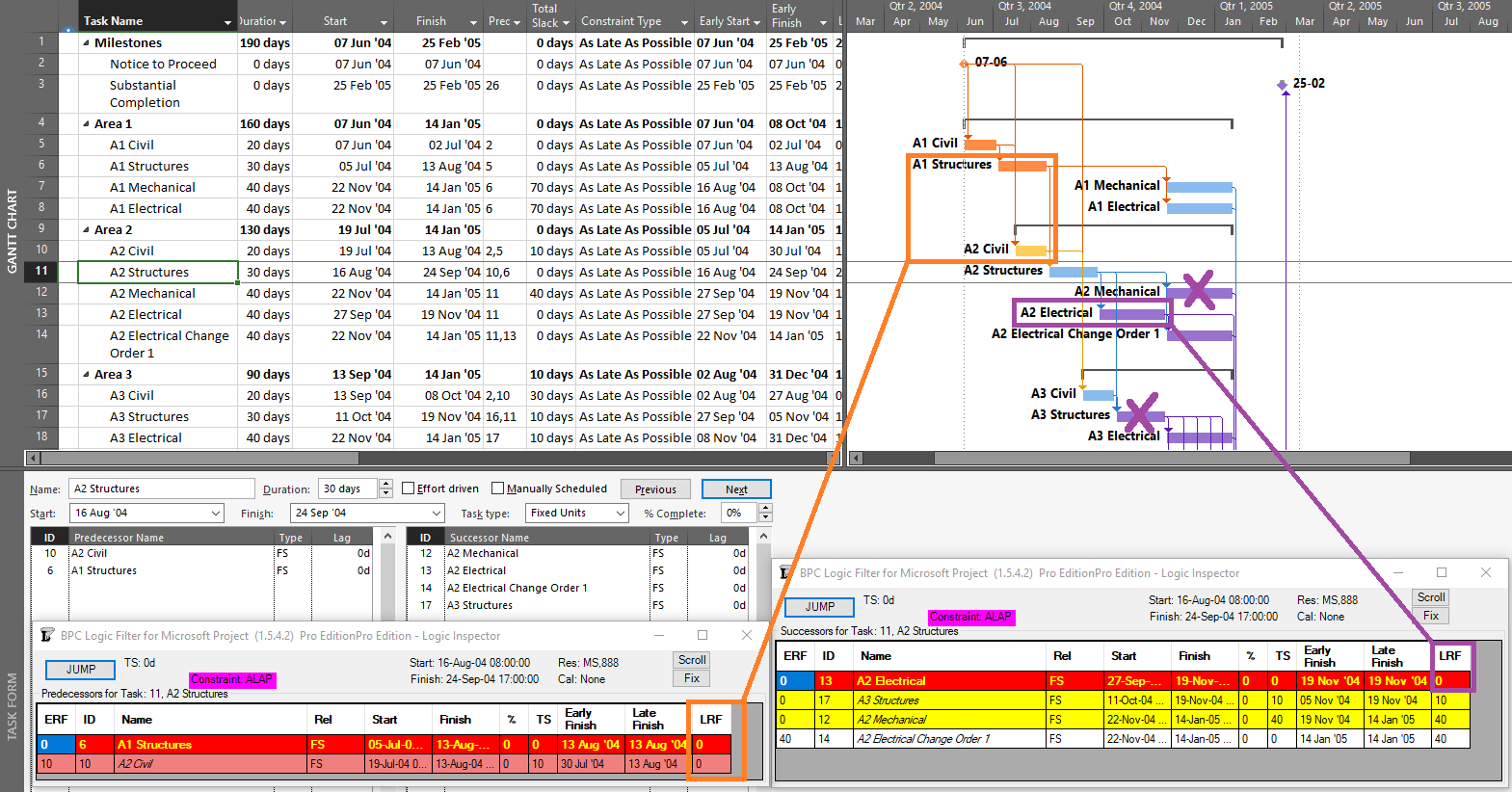
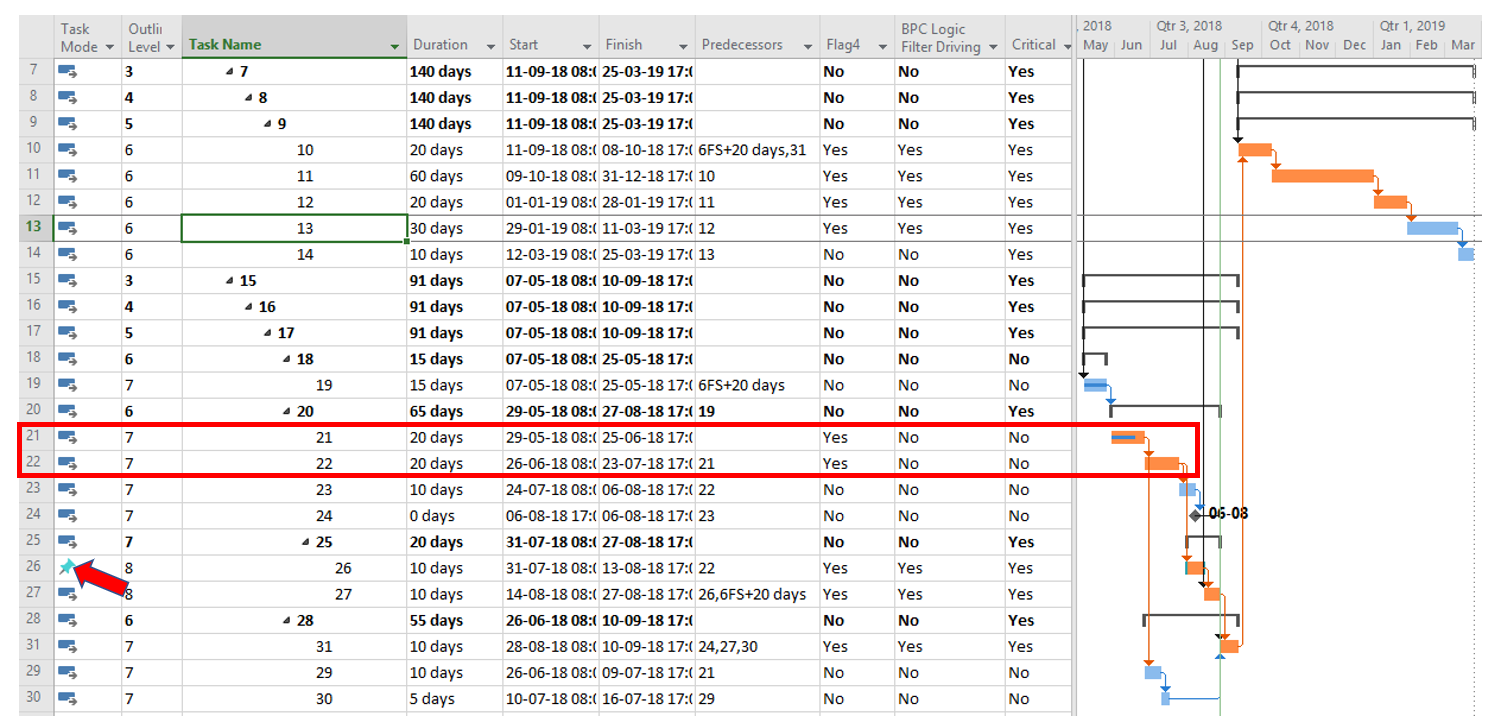
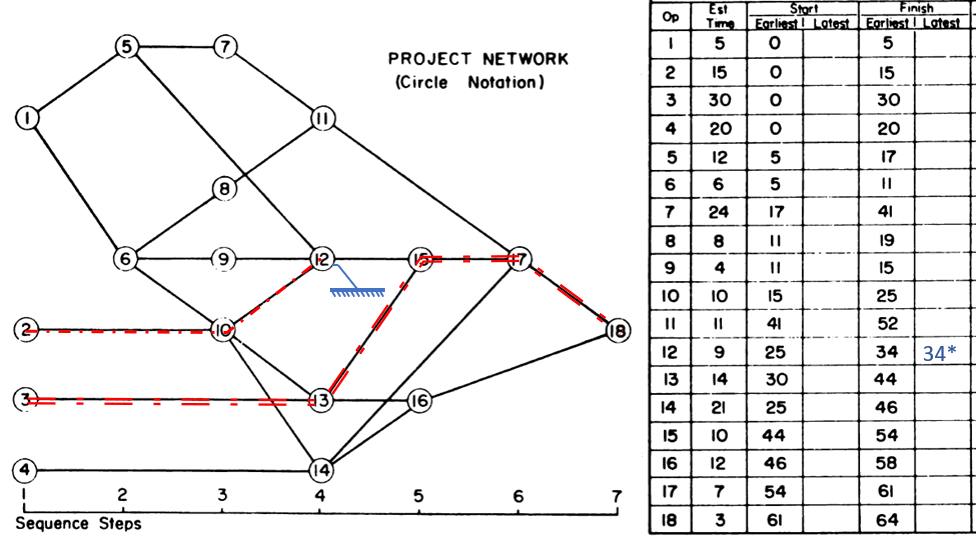
As noted several times here, the methods described for identifying the “longest path” are in fact describing the “driving path to the project finish.” This distinction can raise confusion when one or more activities in the project schedule are delayed by an early constraint. Consider the case below, where an activity on the longest path (Op13) has been delayed 2 days by an early start constraint. Consequently, its sole predecessor relationship (from Op3) is no longer driving, and Op3 gains 2 days of Total Float/Slack. As shown by MSP’s “Driving Predecessor” bar highlighter, the driving logic trace is terminated (going backwards) after reaching the constrained task.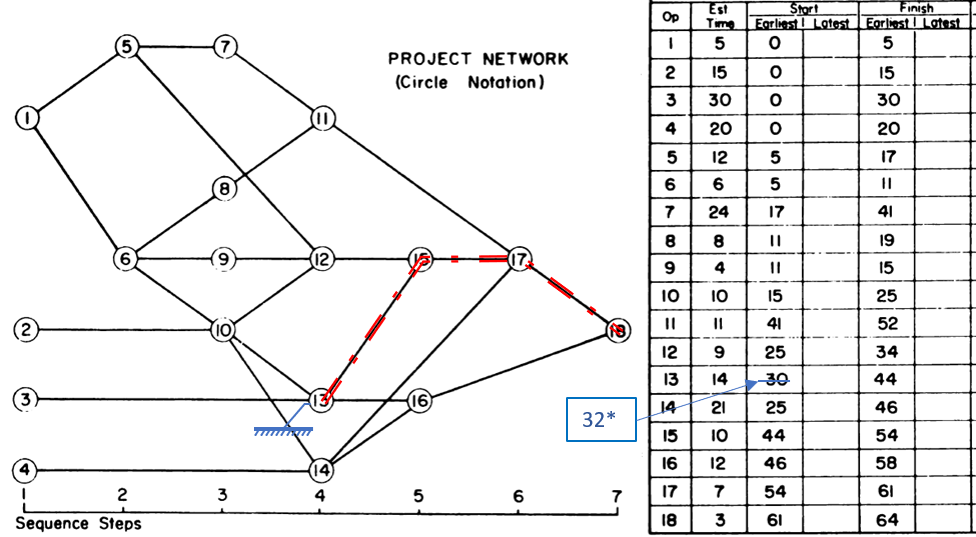
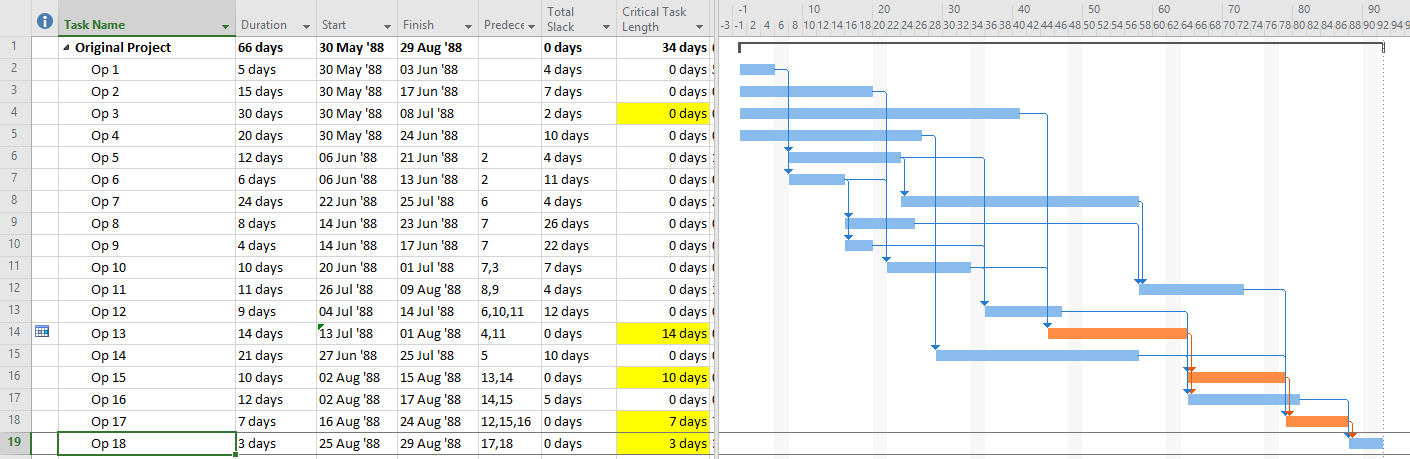
Identical results are obtained from Primavera’s (P6) Longest Path algorithm. This is neither surprising nor incorrect; the project’s completion is in fact driven by the external constraint on Op13, and its predecessor Op3 is quite properly excluded.
In this case, the application of an early constraint on a longest-path task simply truncates the longest path, which may be re-established using a logic tracing routine that jumps the constraint. In general, however, early date constraints can substantially change the driving path to project completion, such that the length (i.e. aggregate duration) of any particular logic path becomes irrelevant. For example, the next figure shows the consequences of imposing a one week (external) delay to Task Op11 in lieu of the earlier constraint. This leads to a 3-day delay of the project’s finish and a shift of the both the driving path and the zero-float path from Task Op13 to Op11. The total length of the corresponding critical path (including Op11’s formerly-driving predecessors) is 62 days. The 64-day path leading through Op13 and Op15 still exists, but it now has 3 days of total slack and is no longer driving the project completion. Thus, the mathematical longest path carries no significance in this constrained project schedule.
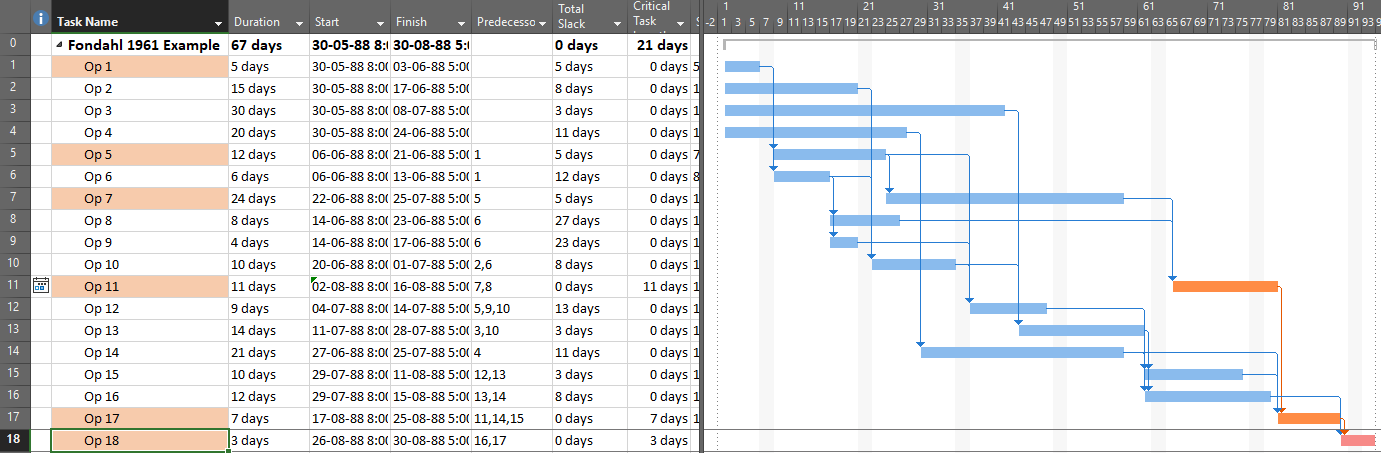
It’s clear therefore that the driving path to project completion and the longest path from the project start (or Data Date) to the project completion can differ when early constraints are present. P6’s “Longest Path” algorithm automatically defaults to the driving path, not the aggregate longest path, and to date there have been no built-in alternatives to that behavior. As a result, some consultants suggest that P6 Longest Path analyses should be rejected when external constraints – even legitimate ones like arrival dates for Customer Furnished Equipment – are present. Unfortunately, a position that requires strict duration-summing to identify critical (i.e. “longest”) paths in schedules containing early constraints appears to be both misleading and inconsistent with standard schedule calculating methods. (A P6 add-in, Schedule Analyzer Software, does claim to provide a true Longest Path representation in the presence of early constraints.)
BPC Logic Filter – Longest Path Filter
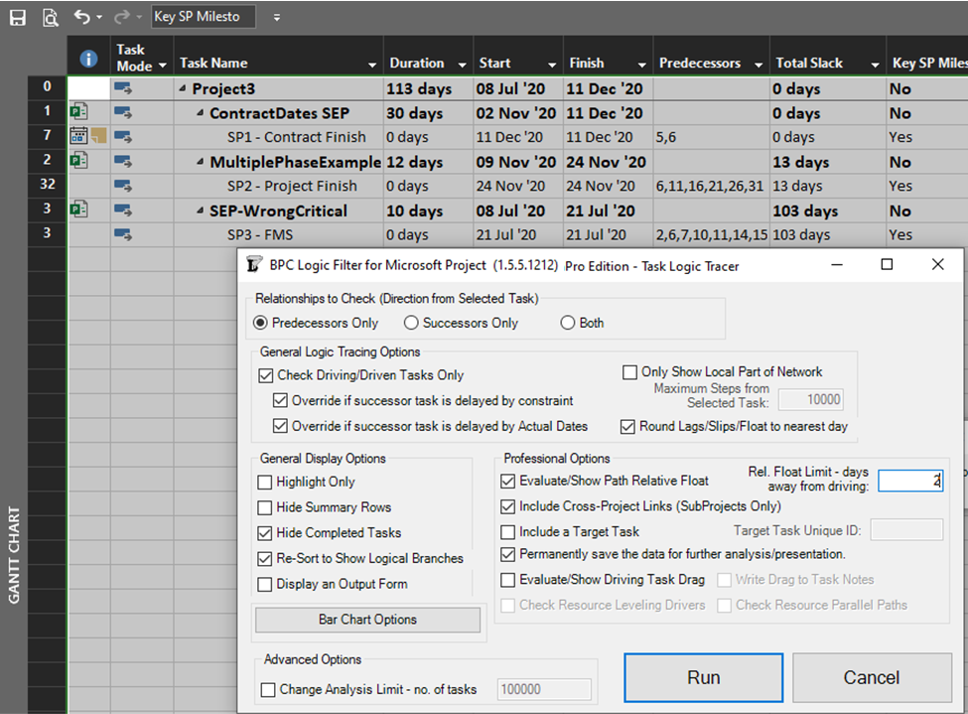
BPC Logic Filter is a schedule analysis add-in for MSP that my company developed for internal use. The Longest Path Filter module is a pre-configured version of the software’s Task Logic Tracer. The module is specifically configured to identify the project’s longest path (as driving path) through the following actions:
- Automatically find the last task (or tasks) in the project schedule.
- Excluding tasks or milestones that have no logical predecessors. (E.g. completion milestones that are constrained to be scheduled at the end of the project but are not logically tied to the actual execution of the project. The resulting trace would be trivial.)
- Excluding tasks or milestones that are specifically flagged to be ignored, e.g. (“hammocks”)
- Trace the driving logic backwards from the last task to the beginning of the project.
- Driving logic is robustly identified by direct computation and examination of relative floats. (Driving relationships have zero relative float according to the successor calendar.) The unreliable StartDriver task objects are ignored.
- Neither completed nor in-progress tasks are excluded from the trace.
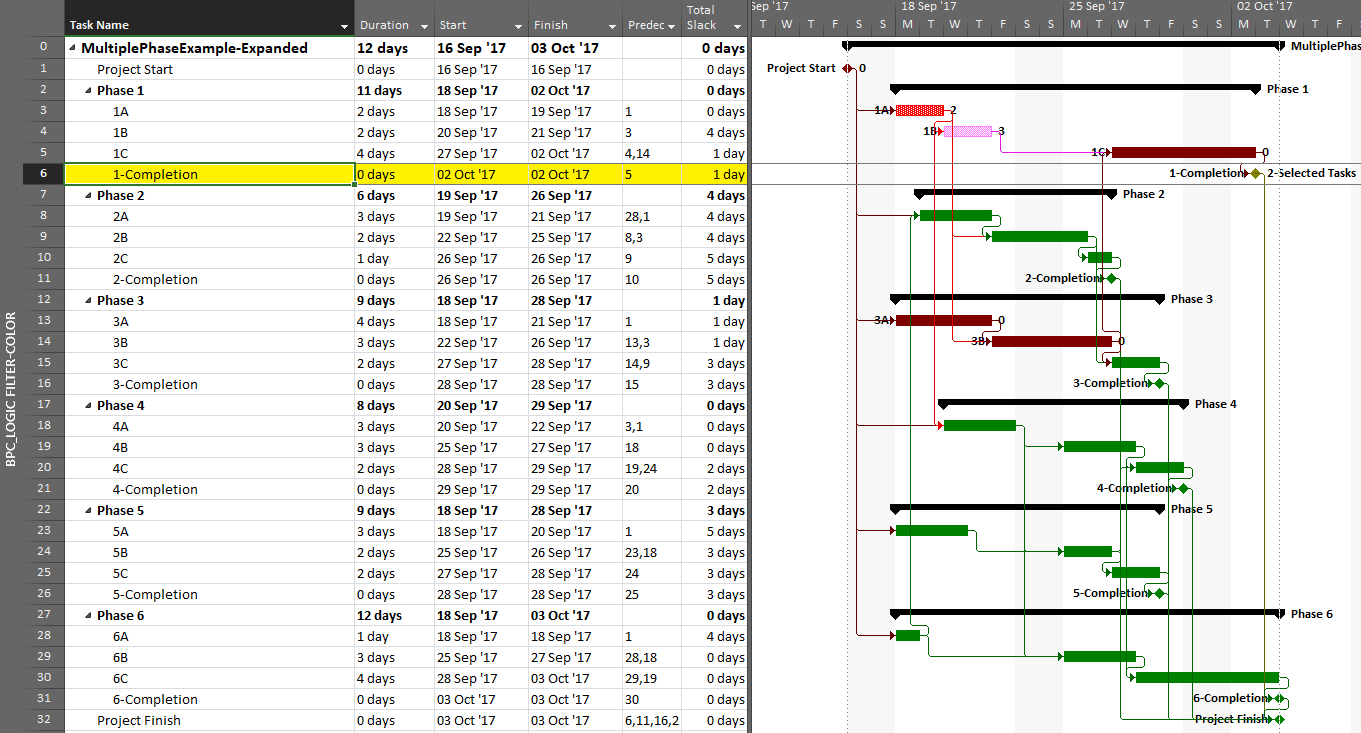
- Either apply a filter to show only the driving logic path, or color the bars to view the driving logic path together (in-line) with the non-driving tasks. The example below is identical to the previous one, but BPC Logic Filter formats the bar chart to ignore the impacts of the applied deadline. The resulting in-line view is substantially identical to the bar chart of the original, unconstrained project schedule.

BPC Logic Filter and the (True) Longest Path
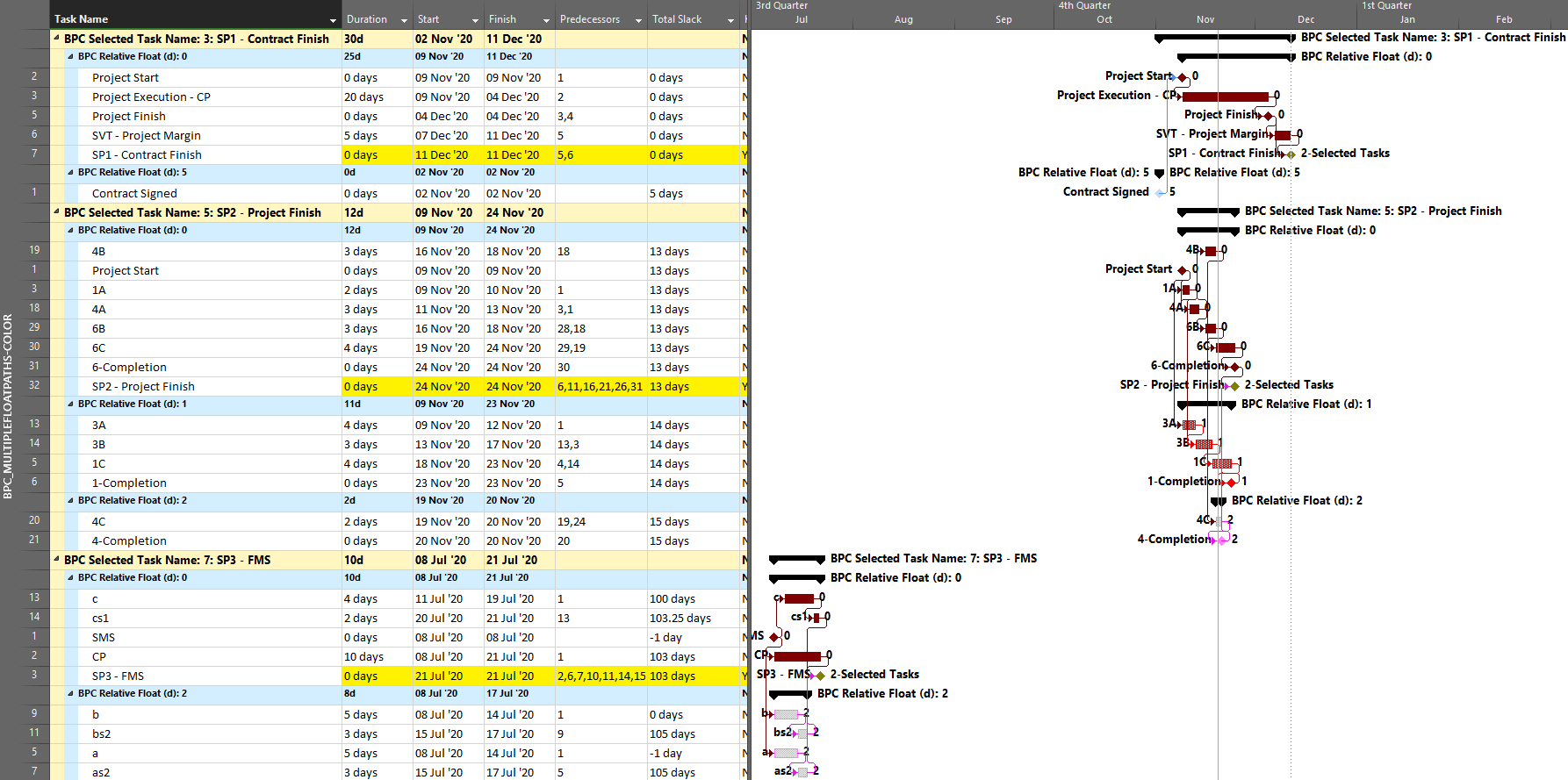
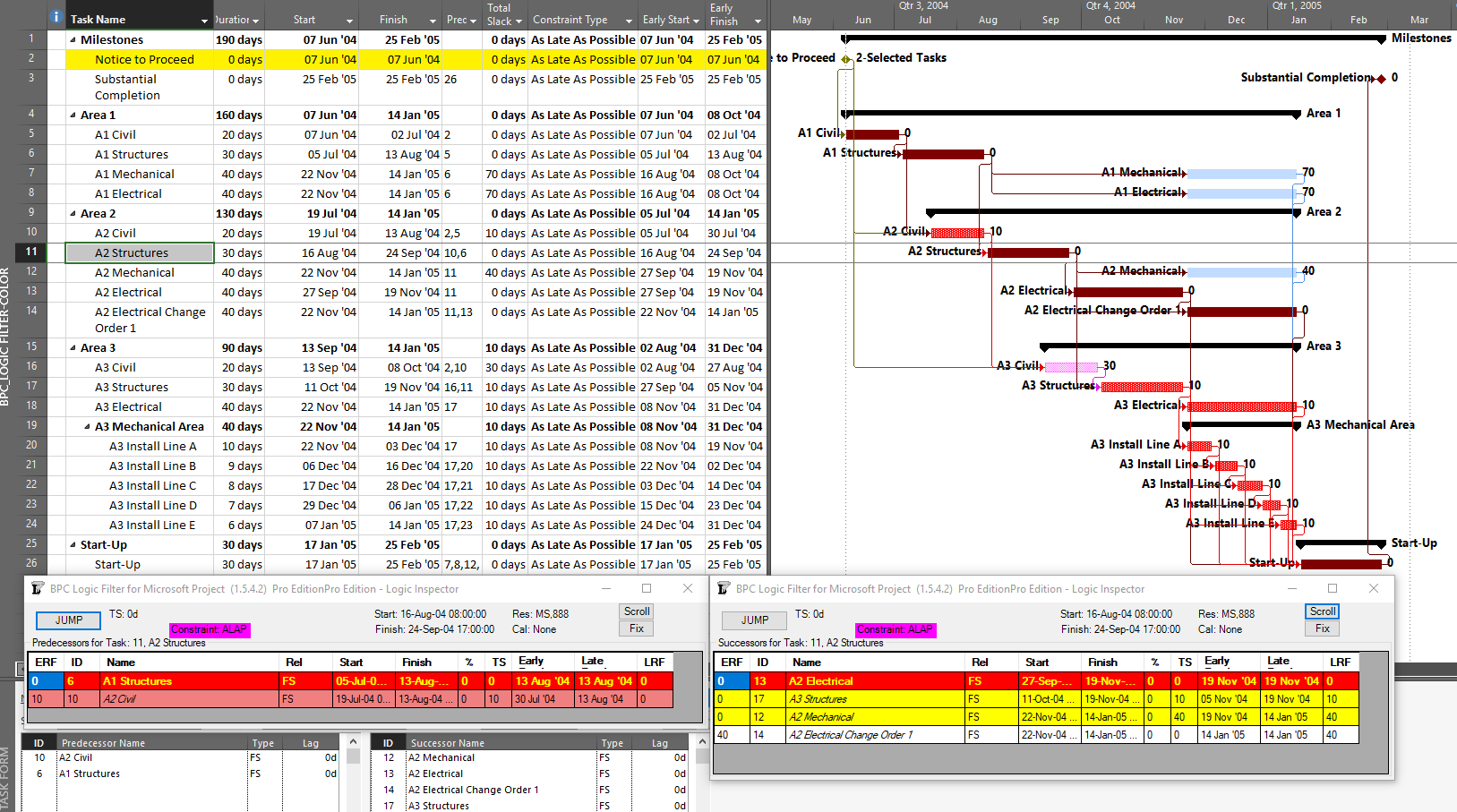
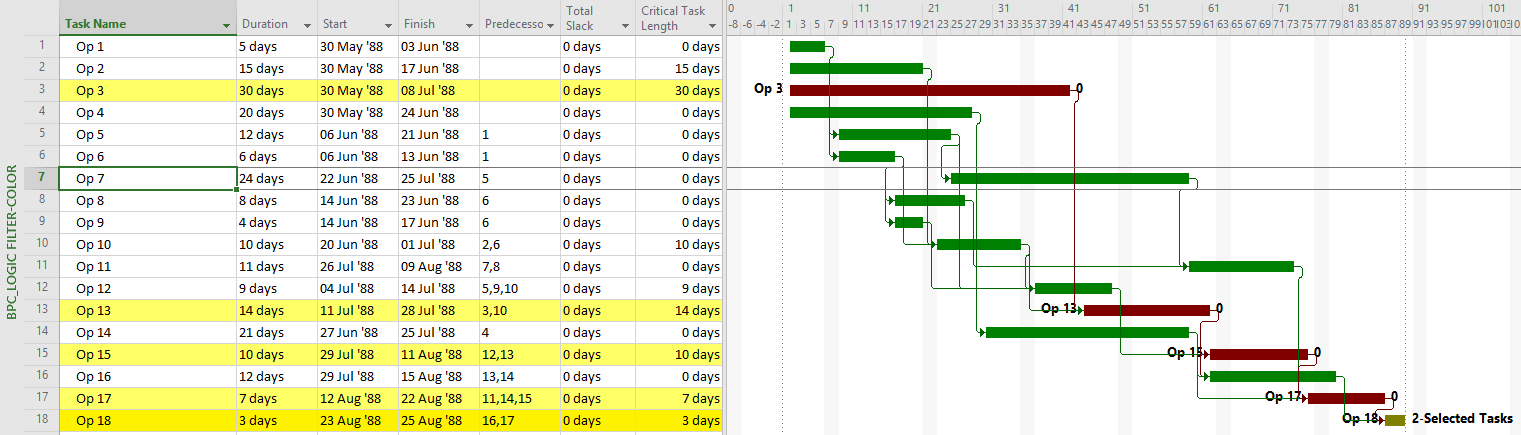
As noted earlier, even a a single early constraint can truncate the driving path to project completion or change the driving path altogether. In either case, it is debatable in my view whether the addition of non-driving, float-possessing activities into the “longest path” makes that term itself more or less useful with respect to the typical uses of the “Critical Path” in managing and controlling project performance. If necessary, it is easy to add such activities – as unconstrained drivers of any constrained task – in BPC Logic Filter by checking a box. The bar chart below shows the results of the Longest Path Filter on the first early-constrained example schedule, as set up according to the driving-path (Primavera) standard. Results are identical to those of the built-in “Driving Predecessors” highlighter in MSP (above) and of P6.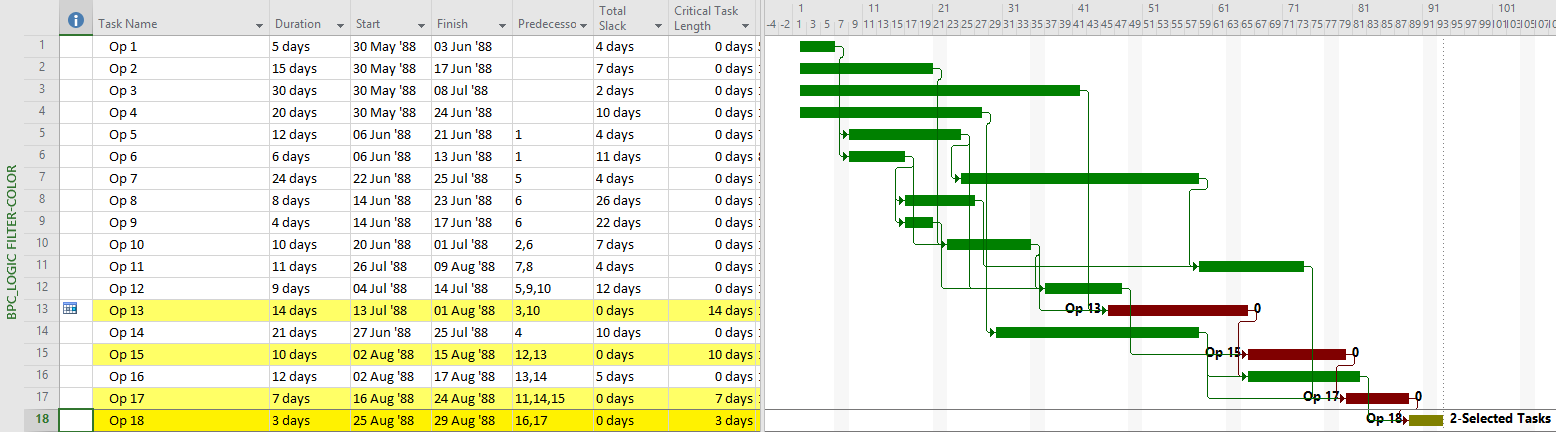
The next chart shows the complete “longest path” for the project, including the non-driving Op3 activity.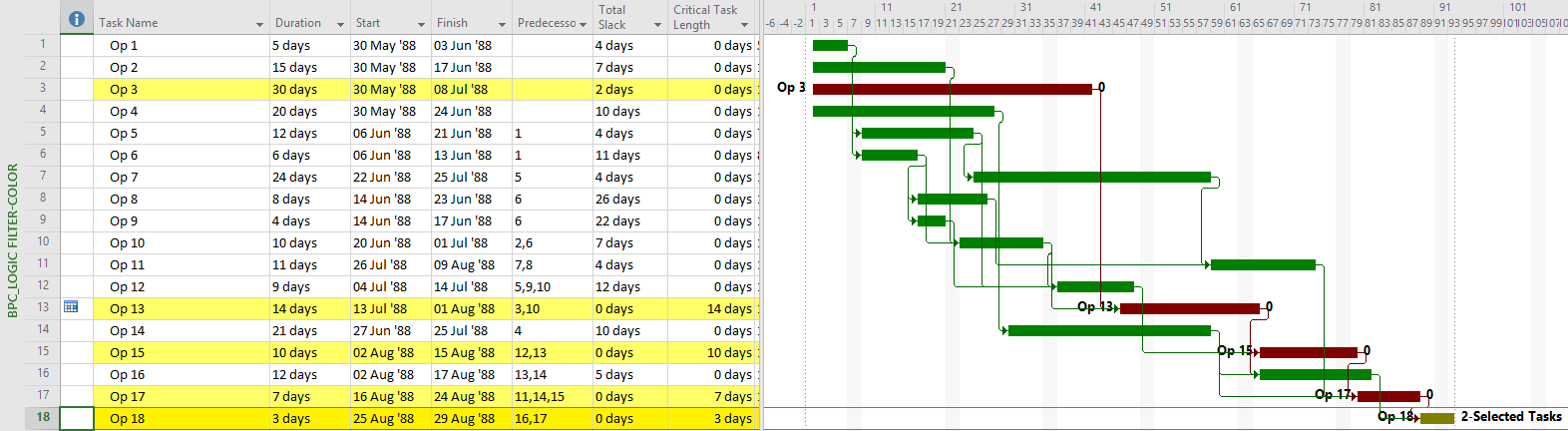
The second chart is different because the check box for “Override if successor task is delayed by constraint” has been checked in the analysis parameters form. Checking the box causes the non-driving predecessor with the least relative float to be treated as driving, and therefore included in the Longest Path, in the event of a constraint-caused delay.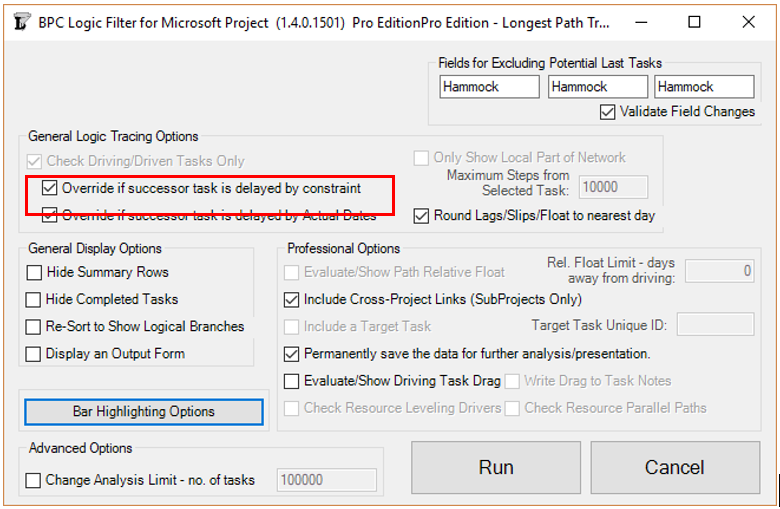
For a quick illustration, see Video – Find the Longest Path in Microsoft Project Using BPC Logic Filter.
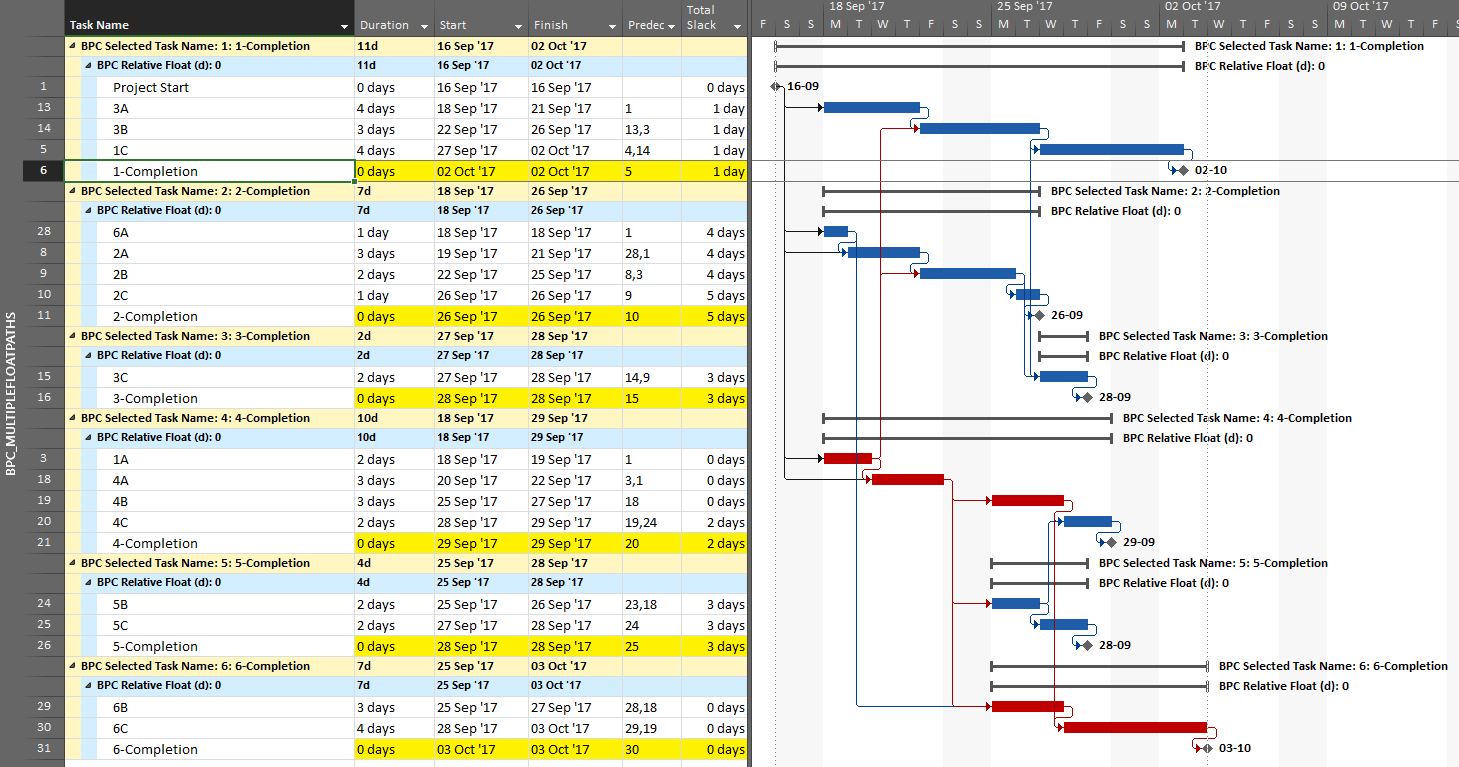
BPC Logic Filter and Near Longest Paths
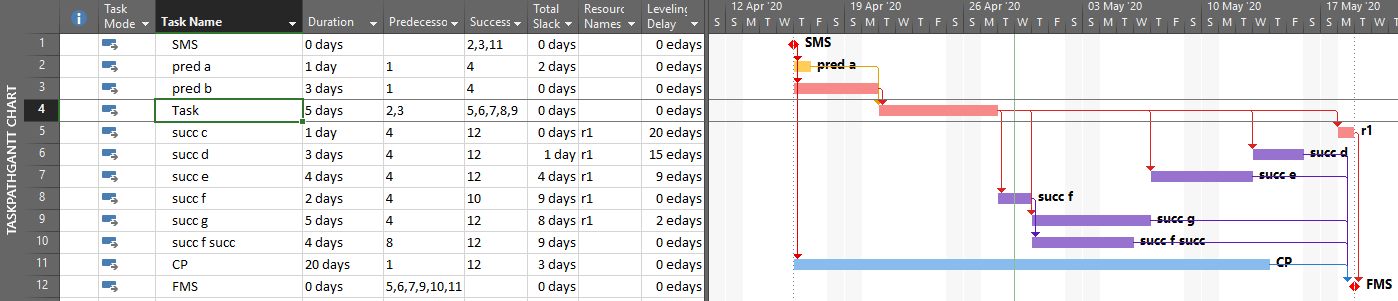
As noted earlier, the normal methods for identifying the “longest path” (i.e. the driving path) in a project schedule have not been generally adopted for analyzing near-longest paths. P6 offers multiple float path analysis, which I wrote about here. In addition, Schedule Analyzer (the P6 add-in mentioned earlier) computes what it calls the “Longest Path Value” for each activity in the schedule – this is the number of days an activity is away from being on the Longest Path (i.e. the driving path to project completion.) In the absence of demonstrated user demand, however, MSP seems unlikely to gain much beyond the Task Path bar highlighters.
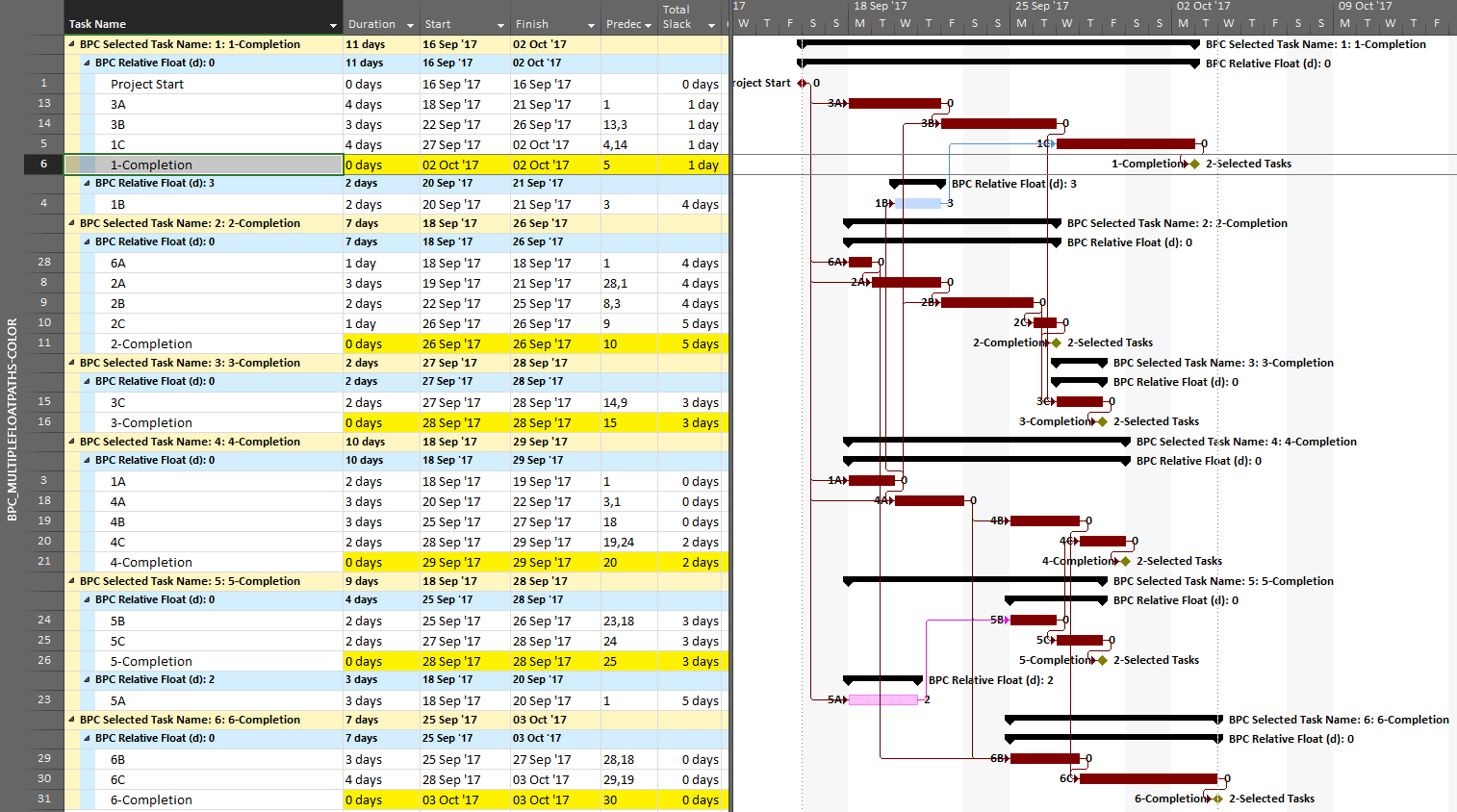
BPC Logic Filter routinely computes and aggregates relative float to identify driving and near-driving logic paths in MSP project schedules. In this context, “near-driving” is quantified in terms of path relative float, i.e. days away from driving a particular end task (or days away from being driven by a particular start task.) Its “Longest Path” and “Near Longest Path” analyses are special cases where the automatically-selected end task is the last task in the project. For the Near Longest Path Filter, tasks can be shown in-line (with bar coloring) or grouped and sorted based on path relative float. The “override if successor is delayed by constraint” setting has no effect when the Near Longest Path Filter is generated. In that case, the non-driving task will be displayed according to its actual relative float. For example Op3 is shown below with a relative float of 2 days (its true value), not 0 days as shown on the earlier Longest Path Filter view.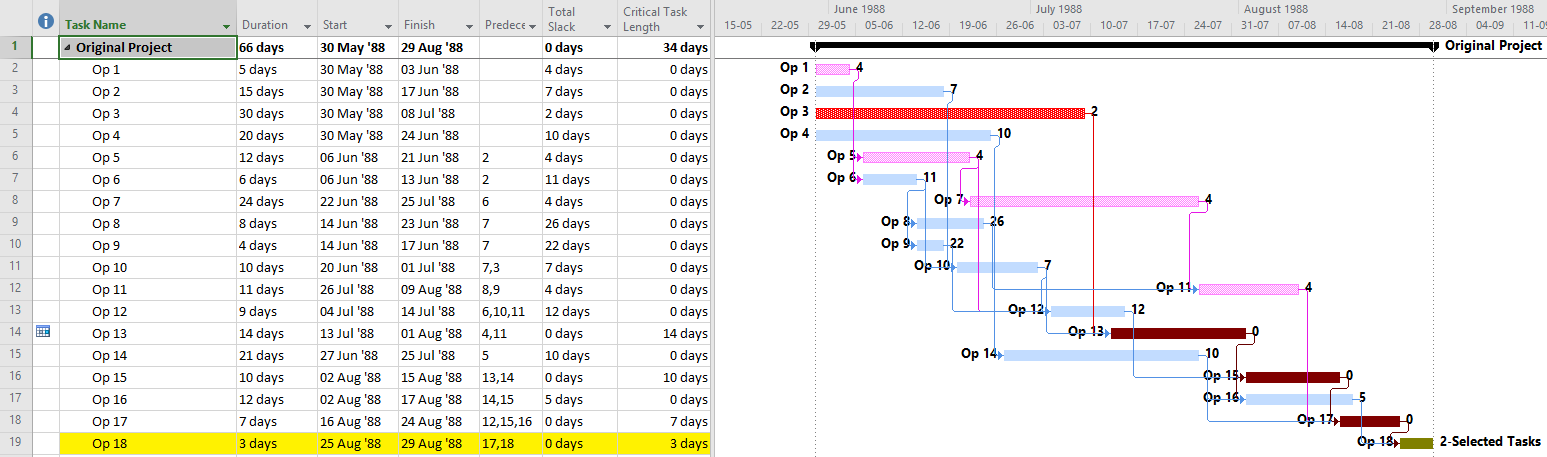
Recap
- In the development of the Critical Path Method, the “longest path” originated as one of several defining characteristics of the “Critical Path” in simple project schedules. Specifically, the “Critical Path” included the sequence of activities with the highest aggregated duration – i.e. the “longest path”. Actual computation and comparison of path lengths was not necessary since relative path lengths could be inferred directly from Total Float – a much easier calculation.
- Complicating factors in modern project schedule networks tend to confuse the interpretation of Total Float, such that it is no longer a reliable surrogate for path length. As a result, the most recent, authoritative definitions of the Critical Path tend to omit references to float while retaining references to “longest path” and, typically, logical control of the project completion date. [Notably, the measurement and comparison of aggregated path durations (path lengths) has not been an explicit feature of any mainstream project scheduling tool, so the “longest-path” part of the definition cannot be definitively tested in general practice.]
- Notions of “longest-path” among current schedule practitioners are heavily influenced by the deceptively-named “Longest Path” feature in Oracle/Primavera’s P6 software. Perversely, that feature DOES NOT aggregate activity durations along any logic paths. Rather, it identifies the driving/controlling logic path to the project’s early finish date.
- The “Longest Path” in P6 (i.e. the Driving Path to Project Completion) and the “longest path” (i.e. the logic path with highest aggregated duration) are NOT equivalent, particularly when the “Longest Path” is constrained by an early date constraint. There is at least one P6 add-in claiming to identify the true “longest path” (and near-“longest paths”) in this case.
- Microsoft Project provides several inefficient methods to identify the Driving Path to Project Completion in simple projects, but these methods are not reliable in the presence of non- Finish-to-Start relationships. There are no native MSP methods for identifying near-driving tasks nor the true “longest path” in the presence of early date constraints. BPC Logic Filter is an MSP add-in that automatically fills these gaps.
- As conceived, the “longest path” criterion implied the transparent calculation and comparison of aggregated activity durations along each logic path in a project schedule. As for Total Float, however, such calculations in complex schedules have been obfuscated by complications like non- Finish-to-Start relationships, lags, and multiple calendars. Since such obfuscation makes path lengths essentially un-testable, it appears that future Critical Path definitions should omit the “longest path” criterion in favor of a simple “driving path to project completion.”
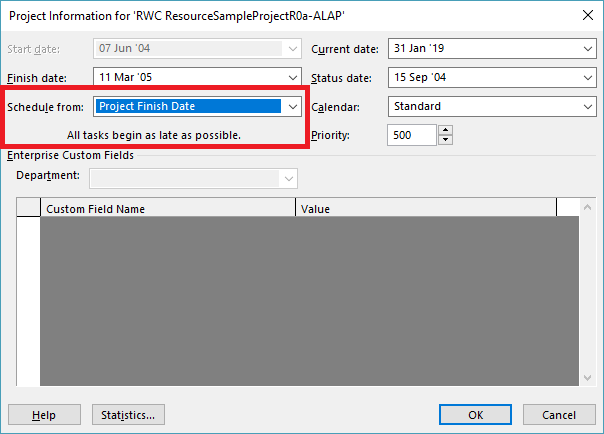
Longest Paths in Backward Scheduled Projects (MSP) [Jan’19 Edit]
As pointed out in this recent article, the Longest Path in a backward scheduled project is essentially the “driven path from the project start,” not the “driving path to project completion.”
For more information, see the following links:
Article – Tracing Near Longest Paths with BPC Logic Filter
Video – Analyze the Near-Longest Paths in Microsoft Project using BPC Logic Filter