Project Planning/Scheduling – Page 4

Inactive Tasks in Microsoft Project

Beware inactive tasks in MSP 2013+, especially if you use non-finish-to-start relationships.

The other day Dominic Moss posted a nice Pulse article over on LinkedIn called Inactive Tasks – more than meets the eye. I liked the article, though I pointed out some fundamental issues with Inactive Tasks that were introduced in MSP 2013. [Note: the link takes you to a new, improved version of Dominic’s article; our original discussion was lost.] Here’s a recap of the lost comments:

“Dominic, this is a nice write-up. I was an early adopter of inactive tasks in MSP 2010 for the reasons you mentioned. With MSP 2013, however, Microsoft introduced a substantial change to schedule calculation around inactive tasks – the program inserts a hidden FS link between inactive task predecessors and successors at run time. I imagine that change persists in 2016. It seems a large number of users complained about the logical consequences of inactivating a task – i.e. its successors lose their driving logical constraints and slide back to the project start date. While the change seems to make life easier for the complainers, users should recognize that inactivating a task does not reliably remove it from the scheduling calculations (except in MSP 2010). That defeats most of their benefits for my purposes…. I stumbled across that ‘feature’ by accident, when a client’s planners (newly upgraded to 2013) started getting different end dates than I was (on 2010) from exactly the same mpp file. We had a number of contingent tasks that were inactivated – some with FF links. MSP 2013 was replacing those FF links with FS links and driving out the project completion!”

So the conclusion is – Beware Inactive Tasks on MSP 2013+.

[Edit: July 2018 – having finally upgraded a dedicated machine to MSP Professional 2016, I can confirm that the program’s updated behavior is a bit more refined than I had experienced with MSP 2013. In the absence of complications caused by lags and multiple calendars, the run-time adjustments generally comply with expectations of a “dissolved” activity. That is, relationships are applied through a zero-duration inactive task – at least on the Forward Pass (the calculations leading to the Early Dates.) This can still extend the scheduled project completion if the inactivated task… 1. was on the driving path to project completion, and 2. possesses reverse logic flow, as in the case of a driven finish and a driving start. Unfortunately, all this sleight of hand seems to wreak havoc on the Backward Pass and the corresponding Late Dates; if the inactive task has a parallel logic path, the late dates (and corresponding Total Slack values) of its predecessors are typically incorrect. Lags and multiple calendars make things even more complex. We’ll have to address all these behaviors in the pending upgrade to BPC Logic Filter, our MSP add-in.]

Musings on Critical Path Drag and Calendars in CPM Schedules

As is the case for Total Float/Slack, introducing variable task calendars can significantly confuse the understanding of Critical Path Drag in Project Schedules.

Video – Compute Critical Path Drag in Microsoft Project]

Critical Path Drag is a useful metric in CPM scheduling that Stephen Devaux introduced in his book Total Project Control, but it is not widely computed or used. Drag represents the individual contribution of any single schedule element (e.g. a task) to the overall duration of a project. By definition, only “Critical Path” tasks have it, and a task’s Drag indicates the total theoretical project acceleration that could be gained if the task’s remaining duration were reduced to zero. Viewed simplistically another way: if Total Float/Slack represents how much a non-critical task may slip before becoming Critical; Critical Path Drag represents how much a Critical task may be compressed* before becoming non-Critical. This can be very useful in focusing a project acceleration (e.g. Crashing) exercise.

It’s clear that theoretically many components in a CPM schedule can possess Drag: activity durations, early constraints, and predecessor lags to start with. Activity calendars can also possess Drag. I originally incorporated Drag analysis into BPC Logic Filter with the aim of correctly analyzing the Drag possessed by each component, but I recently decided to at least temporarily set aside that idea for the following reasons:

Drag seems so rarely used in practice that using even a single number for each activity is a stretch for the typical user; parsing it out to its many components seems unhelpful to most.
Allocating Drag purely by passive network analysis is hard.
Most importantly, other Drag-computing software (namely Spider and Asta) seem to compute only a single figure for each activity. Allocating Drag to different components could conflict with these single-value metrics under some circumstances, leading to confusion and possible loss of confidence in the tool.

Now BPC Logic Filter provides an option to compute a single driving path Drag number for each task included in a logical analysis – using a brute-force, remove-and-recalculate approach. This Drag reflects the maximum acceleration of the project’s completion milestone (or any other selected milestone or task in the project) to be gained by modifying the task’s duration alone. A negative value indicates that the project is shortened by lengthening a particular task – this is reverse logic flow.

As is the case for Float/Slack, introducing variable task calendars can significantly confuse the understanding of Drag. Consider a simple project comprising three 1-day tasks in sequence, beginning on a Friday and with the first two tasks assigned the “Standard” calendar, i.e. 5dx8h. The concluding task “Activity 3” (perhaps a management task) is on a “Monday-Only” calendar.** As shown in the figure below, Activity 3 is scheduled to complete on the second Monday.*** Clearly, removing the duration of Activity 1 (or 2) will accelerate the Completion Task – Activity 3 – by seven calendar days, from the second Monday to the first Monday.

So what is the Drag of Activity 1? As shown by the combined figures below, the answer depends on the calendar used to quantify the acceleration. Measured according to Activity 1’s own calendar, a Monday-to-Monday acceleration is 5 days – indicating 5 days of Drag. That same Monday-to-Monday acceleration is only 1 working day according to the calendar of the Completion Task – resulting in 1 day of Drag. Using the Project’s overall calendar could provide different results altogether. For Activity 3 of this example, the Project Calendar is neither the Local Task Calendar nor the calendar of the Completion Task (also Activity 3); then it becomes like the first two tasks with a Drag of 5 days.

Which is the correct calendar to use? My own preference is to use the calendar of the Completion Task to quantify potential acceleration of the Completion Task (i.e. the middle option above), and this is the default selection in BPC Logic Filter. A detailed logical analysis would assign 1 day of Duration Drag to each of the tasks in the example and a further 4 days of Calendar Drag to Activity 3. There is no logical basis for adding these 4 days of Calendar Drag to any other task, but using a mismatched calendar in a brute-force Drag analysis does exactly that, as shown in the top and bottom options above. Those options remain in BPC Logic Filter to allow consistent comparisons with Drag calculations from other tools.

*In the absence of constraints, variable calendars, and certain relationship lags; the compression of a particular Critical Path task can lead directly to compression of the project. Then the idea that Drag represents the potential productive compression of the task itself (i.e. the mirror image of Total Float/Slack) can appear true. Such a simplified view should not be generalized for complex projects, however.

**Credit and thanks for this example go to Vladimir Liberzon of Spider Project. Spider is one of the few scheduling tools to compute Drag.

***Project correctly computes Total Slack of 4 days for the first two tasks, meaning they could each slip 4 days – according to their own calendars – without delaying the project. MSP marks them non-Critical. They are nonetheless on the driving path to project completion, as shown by BPC Logic Filter, and they possess Drag.

No Summary Tasks on the Critical Path – Calculating Total Slack for Summary Tasks in Microsoft Project

Total Slack as presented in Microsoft Project is not a valid metric for logical analysis of Summary Tasks. Users are advised to ignore it.

Underlying the “automatic” project scheduling in Microsoft Project are some simple mathematical processes that are commonly referred to as the Critical Path Method (CPM). CPM schedule calculation starts with a “Forward-Pass” through the schedule network to identify the earliest POSSIBLE start and finish dates that can be scheduled for each task – subject to its calendars, predecessors, and early constraints. Next – starting from the project completion – comes the “Backward-Pass” to identify the latest ALLOWABLE start and finish dates for each task, subject to its calendars, successors, and late constraints. For each task the difference between the late and early dates is called “Slack”.

“Start Slack” = Late Start – Early Start

“Finish Slack” = Late Finish – Early Finish

“Total Slack” = the lesser of Start Slack or Finish Slack (with some exceptions).

In traditional CPM, the “Critical Path” – i.e. that collection of tasks that controls the completion date of the project – is identified using Total Slack according to one of the following definitions depending on the complexity of the project and other factors:

Total Slack = 0; or
Total Slack = the lowest observed value.

Microsoft Project identifies critical tasks based on Total Slack <=0 (or some other threshold). [As noted in another post, this often leads to an incorrect identification of Critical Path for a project.]

Summary tasks are not anticipated in traditional CPM algorithms, so calculation and interpretation of Slack/Float for summaries can vary significantly between scheduling tools. In some (or most) CPM tools, summaries exist primarily to roll-up cost and schedule data (including slack/float) from the underlying sub-tasks. In Project, however, each summary task exists first as a task in its own right, with corresponding logical and hierarchical relationships to other tasks. This leads to common misunderstandings of exactly what is meant by “Total Slack” of a summary task in Microsoft Project.

In general, the following observations hold true for MSP 2010 Professional:

Each summary task inherits its early and late dates from its sub-tasks according to the following:
1. Early Start = the earliest Early Start of all the sub-tasks;
2. Late Start = the earliest Late Start of all the sub-tasks*;
3. Early Finish = the latest Early Finish of all the sub-tasks;
4. Late Finish = the latest Late Finish of all the sub-tasks*.
  [* Behavior shown is for normal scheduling, i.e. schedule from project start with ASAP constraints.]
The Start Slack, Finish Slack, and Total Slack of the summary task are computed according to the inherited early and late dates.
Since Total Slack of the summary task is derived from up to four different, logically unconnected sub-tasks, it has no significance with respect to the Critical Path or any other logic path in the project schedule. This is illustrated in the figure above: Summary task B inherits its Early Start and Late Finish from task B1 and inherits its Late Start and Early Finish from task B4. The resulting 4 days of Total Slack shown for the summary task reflects the difference between the Late Finish of task B1 and the Early Finish of task B4 – completely meaningless in the absence of any logical connections between the two tasks. The 4 days of Total Slack for the summary task is also unrelated to the Total Slack values of any of its underlying sub-tasks.
If the summary task possesses logical successors – or if its parent or any outline-ancestor summary tasks possess logical successors – then the late dates can be further accelerated through hierarchical inheritance. The result is total slack that is sometimes zero or negative.
If the summary task possesses a manually-scheduled sub-task whose start date precedes that of any other sub-task under the summary, then the manual sub-task’s scheduled start date will be written to both the early and late start of the summary task, resulting in zero start (and total) slack.

Some tools have allowed summaries to display the “most-critical” (or lowest) float of the associated activities – which at least means something. Similar behavior may be obtained in Microsoft Project by inserting a custom duration field – say “Rolled Up Total Slack” – using a simple formula (“=[Total Slack]”) with “Rollup” set to Minimum.

Many modern MSP schedules incorporate variable calendars, deadlines, late constraints, or resource leveling; and the basic CPM assumptions no longer apply. Under such conditions Total Slack for any task – summary or sub-task – becomes unreliable for identifying the Critical Path or any other logical path through the schedule. That’s when a utility like BPC Logic Filter is needed.

Simple Macro for Imposing Zero Free Float Constraints in Microsoft Project

Here I outline a method – including the ImposeZFF macro – to provide “just-in-time” scheduling of flagged tasks in MSP. I also include a separate macro, RemoveZFF, to restore the tasks to as-soon-as-possible scheduling.

Another missing feature for anyone coming to MSP from Primavera’s planning tools is the “Zero Free Float (ZFF)” constraint. (Primavera now calls this the “As Late as Possible (ALAP)” constraint – NEVER to be confused with MSP’s identically-named version, which is pretty useless for forward scheduling.) The ZFF constraint delays an activity as much as possible without impacting any successor activities. It is useful for scheduling just-in-time works and deliveries while preserving the correct logic flow through the project schedule.

Consider the simple project shown here. The overall project completion is limited by a constraint on task B. (I never use such mandatory constraints in practice but use it here to avoid having to add other extraneous logic to the example.) Task A must be completed before B, but for maximum efficiency it is desired to perform this work just-in-time. Because MSP has no other obvious feature to arrive at the desired schedule outcome, the scheduler is tempted to make task A a Start-to-Finish successor of B. Such an approach is unsound and is to be avoided for a number of reasons. All links in a logic-driven project schedule must reflect real logical constraints, and real Start-to-Finish constraints are extremely rare.

So what is the scheduler to do? Most situations are easily solved by adding logical milestones to the project schedule. For example, a logic-driven “Site Ready for Delivery” milestone as a Finish-to-Finish predecessor of “Eqpt Delivery” would be quite normal. In the very few occasions when suitable logical workarounds cannot be devised, then it may be useful to impose early-start constraints to achieve the zero-free-float objectives. For good control over the process, I use a custom flag field to designate specific tasks requiring ZFF constraints. Then I run a macro that automatically computes and assigns the appropriate constraint to all the ZFF tasks in the project at once. This makes ZFF constraints easy to audit, review, and justify.

For our simple project example, I inserted the Flag20 local field into the Gantt Chart entry table and called it ZFF. Then I marked task A with the ZFF flag and ran the macro. The macro automatically imposed a new early-start constraint on the task. As a result, the 12 days of Total Slack (like the 12 days of Free Slack) that previously existed have been consumed. Task A is now correctly shown as Critical.

If your project has a logical chain of tasks that are all ZFF-flagged, then you’ll have to re-run the macro several times (or add a simple iteration loop to the code. I have one but didn’t include it here for simplicity.)

[May 2019 Edit: Though I don’t use this macro, one user has reminded me that when used to delay a string of connected tasks, selecting the tasks in reverse order may be more efficient than the forward order first included in this article. I.e. use the “For i…” block shown here in place of the “For each t” block originally included. I might get around to modifying that code eventually.]

    Dim i As Long
    For i = ActiveProject.Tasks.Count To 1 Step -1
        Set t = ActiveProject.Tasks(i)
        If Not t Is Nothing Then

            'If t.GetField(Application.FieldNameToFieldConstant(FieldName))....
               '...
               '...
             End If  
        End If
    Next i

The code for imposing the constraints is shown below. Drop it into a VBA module in your Global.mpt file (or in a specific .mpp file if necessary), then look for and run macro “ZFFImpose”. I normally use another function to find the ZFF flag field in a project, but that function was too big to include here. So if you want to use a custom flag field other than Flag20, just change the “FieldName = “Flag20″” statement in the code.

Sub ZFFImpose()
' Macro Coded 31-08-16 by Thomas Boyle PE PSP PMP.
On Error GoTo 0
    
    Dim i As Integer
    Dim t As Task
    Dim L1 As String
    Dim L2 As String
    Dim SW1 As Boolean
    Dim SW2 As Boolean
    Dim SW3 As Boolean
    Dim FieldName As String
    
    'FieldName = FindField_Flag("ZFF") 'Function not included here
    Fieldname="Flag20"
    If FieldName = "" Then
        MsgBox Prompt:="No ZFF Flag Field Found", Title:="ZeroFreeFloat Constraints"
        Exit Sub
    End If
                
    CalculateProject

        For Each t In ActiveProject.Tasks
            If Not t Is Nothing Then
                If t.GetField(Application.FieldNameToFieldConstant(FieldName)) = "Yes" Then
                    If t.FreeSlack > 0 Then
                        t.ConstraintType = pjSNET
                        If t.Calendar = "None" Then
                            t.ConstraintDate = Application.DateAdd(t.Start, t.FreeSlack)
                        Else
                            t.ConstraintDate = Application.DateAdd(t.Start, t.FreeSlack, t.CalendarObject)
                        End If
                        CalculateProject
                        L1 = L1 & t.ID & " " & t.Name & " " & t.ConstraintDate & vbCrLf
                        SW1 = True
                    Else
                        L2 = L2 & t.ID & " " & t.Name & vbCrLf
                        SW2 = True
                    End If
                End If
            End If
        Next t
    GoTo Finish

tEHandler:
    MsgBox ("Failed to impose Zero Free Float Constraints")
    Exit Sub
    
Finish:
    CalculateProject
    If SW1 = True Then MsgBox Prompt:="Imposed Early Start Constraints to remove free float:" & vbCrLf & L1, Title:="ZeroFreeFloat Constraints"
    If SW2 = True Then MsgBox Prompt:="No free float to remove on tasks: " & vbCrLf & L2, Title:="ZeroFreeFloat Constraints"
    If SW1 = False And SW2 = False Then MsgBox Prompt:="No tasks marked for ZFF", Title:="ZeroFreeFloat Constraints"
    
End Sub

What is done with the “ZFFImpose” macro is easily undone with the “ZFFRemove” macro shown below. This macro returns all ZFF-flagged tasks to “As Early As Possible” scheduling.

Sub ZFFRemove()
' Macro Coded 31-08-16 10:30 by Thomas Boyle PE PSP PMP.
On Error GoTo 0
    
    Dim t As Task
    Dim L1 As String
    Dim SW1 As Boolean
    Dim FieldName As String
    
    FieldName = "Flag20"
    'FieldName = FindField_Flag("ZFF")
    If FieldName = "" Then
        MsgBox Prompt:="No ZFF Flag Field Found", Title:="ZeroFreeFloat Constraints"
        Exit Sub
    End If
                
    For Each t In ActiveProject.Tasks
        If Not t Is Nothing Then
            If t.GetField(Application.FieldNameToFieldConstant(FieldName)) = "Yes" Then
                If t.ConstraintType = pjSNET Then
                    t.ConstraintType = pjASAP
                    CalculateProject
                    L1 = L1 & t.ID & " " & t.Name & vbCrLf
                    SW1 = True
                End If
            End If
        End If
    Next t
    GoTo Finish

tEHandler:
    MsgBox ("Failed to remove Zero Free Float Constraints")
    Exit Sub
    
Finish:
    CalculateAll
    If SW1 = True Then MsgBox Prompt:="Removed Early Start Constraints from designated ZFF tasks:" & vbCrLf & L1, Title:="ZeroFreeFloat Constraints"
    If SW1 = False Then MsgBox Prompt:="No tasks marked for ZFF", Title:="ZeroFreeFloat Constraints"
End Sub

Float is not Schedule Contingency, Except when it is

I am writing this as a reminder to myself and to colleagues.

Total Float is NOT schedule contingency. That’s right: Total Float is NOT schedule contingency. I say this after the umpteenth conversation with a very smart and experienced contractor who regularly uses the terms interchangeably.

First, a couple references:

Merriam-Webster

Merriam-Webster defines “contingency” as a Noun thus:

1: a contingent event or condition: such as

a: an event (such as an emergency) that may but is not certain to occur

b: something liable to happen as an adjunct to or result of something else

2: the quality or state of being contingent

When budgeting projects, our usage of the term has evolved from an “allowance for contingencies”, through “contingency account”, to often a simple “contingency” amount – setting aside funds for uncertain costs or unknown risks in project scopes. Similarly, a “schedule contingency” exists as an explicit setting-aside of time to address uncertain durations or risks in project schedules.

AACE

AACE International (formerly the Association for the Advancement of Cost Engineering International) issued a Recommended Practice for Schedule Contingency Management (70R-12) that defines schedule contingency as, “an amount of time included in the project or program schedule to mitigate (dampen/buffer) the effects of risks or uncertainties identified or associated with specific elements of the project schedule.” Then the RP emphasizes, “Schedule contingency is not float (i.e. neither project float* nor total float).” Finally, the RP goes on to define Project Float (in a footnote) as, “the length of time between the contractor’s forecast early completion and the contract required completion.” A key theme of the recommended practice is to make schedule buffers explicit, visible, and allocated to specifically identified schedule risks.

* I might quibble with the “project float” exclusion, particularly in any case where risk mitigation is its primary motivation.

ASCE

The American Society of Civil Engineers recently published a new standard: ANSI/ASCE/CI 67-17 – Schedule Delay Analysis. Page 5 of this new standard provides a fairly long definition of “Float” that seems essentially correct with the pronounced exception of its first clause, “Float — The time contingency that exists on a path of activities.” Obviously, this is a direct contradiction to the AACE definition above. It also appears largely at odds with the rest of the definition in the ASCE standard.

DCMA

The Defense Contract Management Agency (DCMA) promulgated a 14-Point Assessment methodology for analysis of Integrated Master Schedules, which seems to have been widely adopted in some industries.

Point 13 of the DCMA’s 14-Point Analysis defines the Critical Path Length Index (CPLI) as:

Critical Path Length + Total Float

CPLI = ____________________________________

Critical Path Length

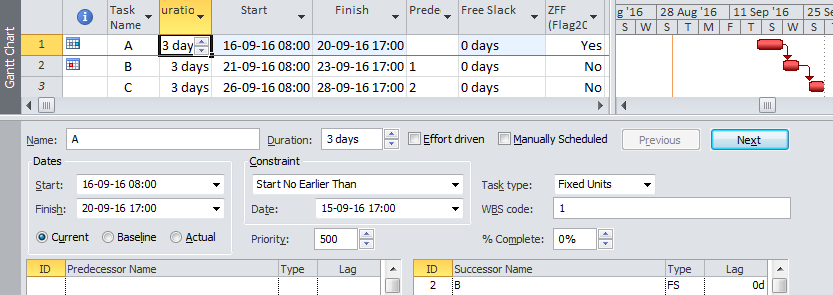
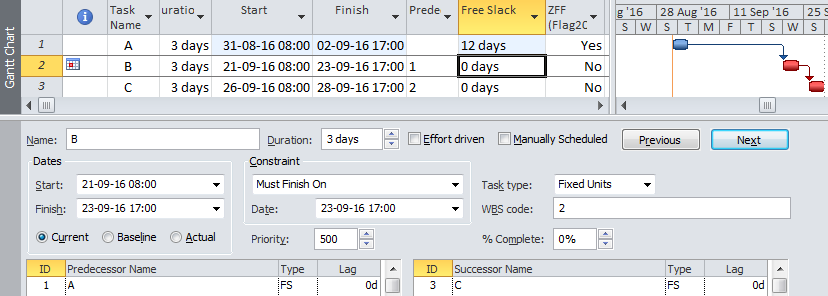
Here the “Critical Path Length” is essentially the time (in days) from the current data/status date until the forecast completion date of the project. The “Total Float” used in the ratio turns out to be the difference between the forecast completion date and the baseline/contract completion date – we otherwise know this as “Project Float.” (This is also the value of Total Float that Oracle’s Primavera P6 scheduling software displays on the Critical Path when a Project “must finish by” constraint corresponding to the contract completion date is assigned.)

The DCMA guidance provides a target value of 1.00, corresponding to a Project Float of 0. It goes on to suggest that a CPLI greater than 1.00 (i.e. Project Float is positive) is favorable while a CPLI less than 1.00 (i.e. Project Float is negative) is unfavorable.

NEC ECC

The NEC Engineering and Construction Contract (ECC), a collaborative contract form with increasing use in UK and Commonwealth countries, has formalized the use of two alternate terms for schedule contingencies:

Terminal Float

Terminal Float is the difference between the current Planned Completion date and the (Contract) Completion Date. It is not of a fixed size, is not allocated to any particular risk(s), and is reserved for the exclusive use of the Contractor. Notably, an acceleration of early activities that results in acceleration of the Planned Completion date also increases the Terminal Float. Terminal Float is equivalent to the Project Float of AACE International terminology.

Time Risk Allowance

Time Risk Allowance (TRA) “is made by the contractor when preparing its programme. These are owned by the contractor and provided to demonstrate that the contractor has made due allowance for risks which are the contractor’s under the contract. They must be realistic – unrealistic allowances could prevent the project manager from accepting the programme.” In other words, TRA is explicit time contingency buffer/allowance that is allocated to specific activities and risk events in the project schedule.

Clause 31 of the NEC Engineering and Construction Contract (ECC) requires the Contractor to show float and “time risk allowance” (TRA) on the programme (i.e. schedule). The NEC does not specify exactly how to “show” the TRA, though the demand that it be “realistic” has been used to justify a requirement that TRA be distributed through the project schedule based on explicit risk assessment (like the AACE RP). Typically, the TRA is included in padded activity durations, with the specific TRA portion explicitly noted in a custom field for each activity. In any case, the TRA participates directly (as a duration) in the CPM calculations for the deterministic project schedule, an output of which is Float. (Obviously, it must be excluded from any schedule risk simulations.)

Confusion

The mixed definitions have led to some confusion and contradictory recommendations from professionals.

The ASCE document on Schedule Delay Analysis implies that “time contingency” simply exists, manifested as Float, on a network path. This is far from the common use of “contingency” as an explicit and proactive allowance for risk.

In the NEC environment, there seems to be a persistent tendency to conflate TRA with various types of Float, with some reputable legal sources describing both Terminal Float and “Activity” float as “leeway the contractor adds” in case of problems. In some cases, contractors are being advised to explicitly mis-identify activity Free Float as Time Risk Allowance in their project schedules, thereby reserving that portion of the activity’s Total Float for themselves.

My View:

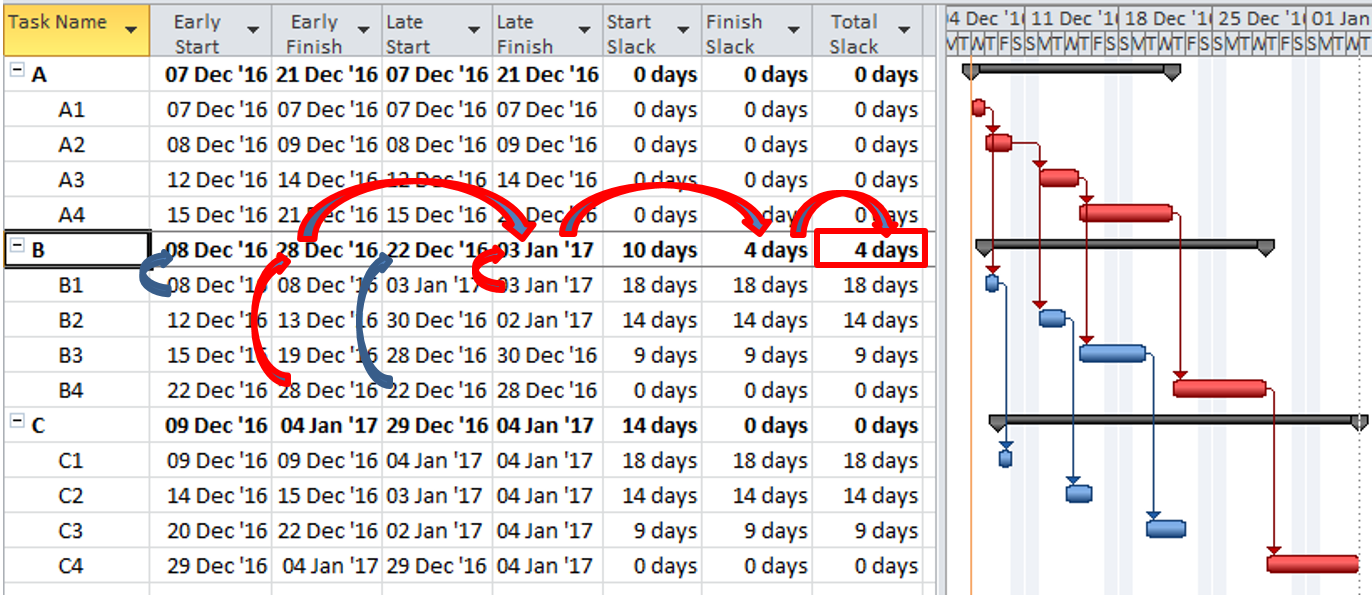
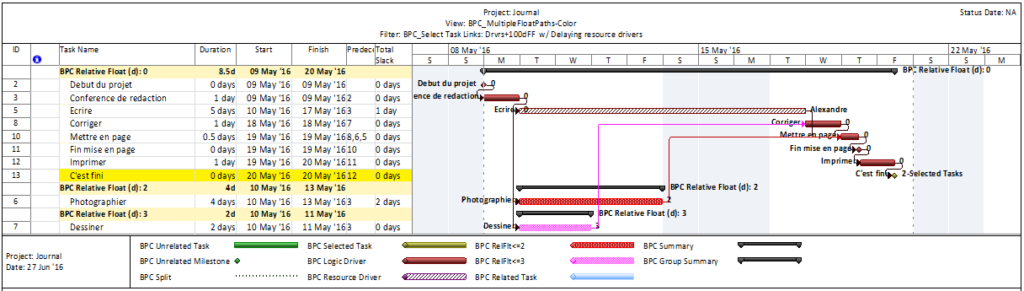
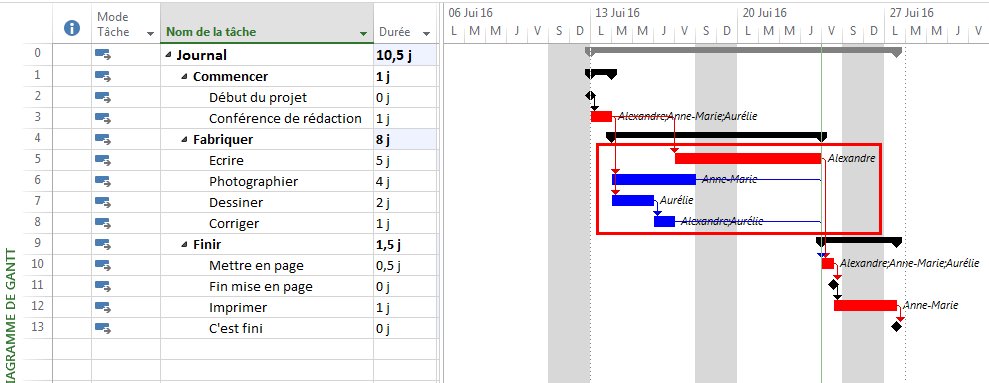
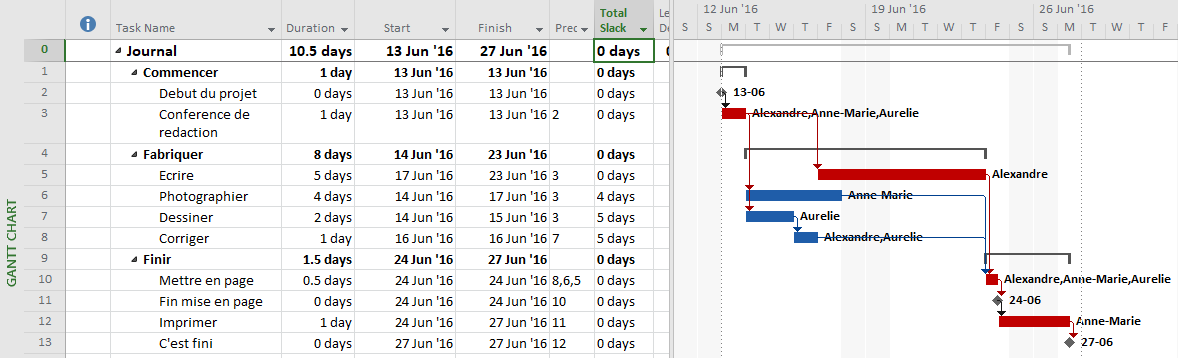
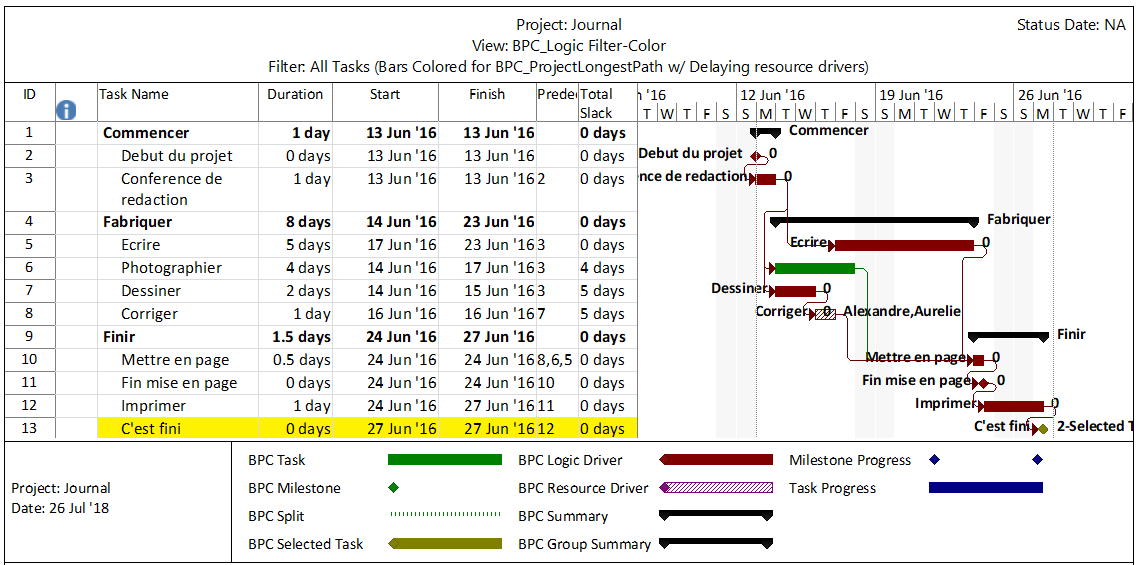
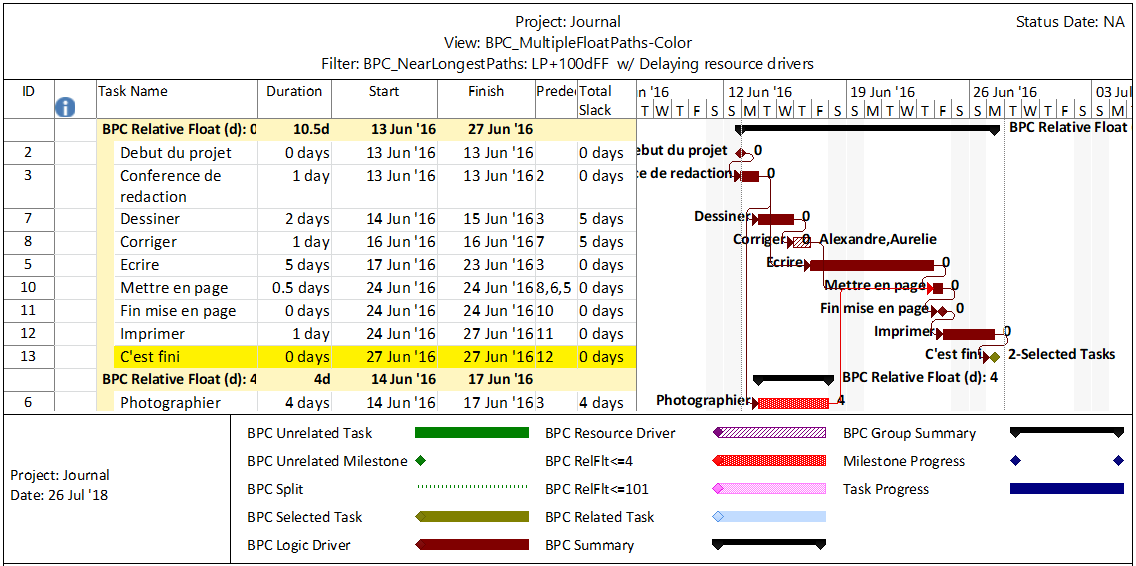
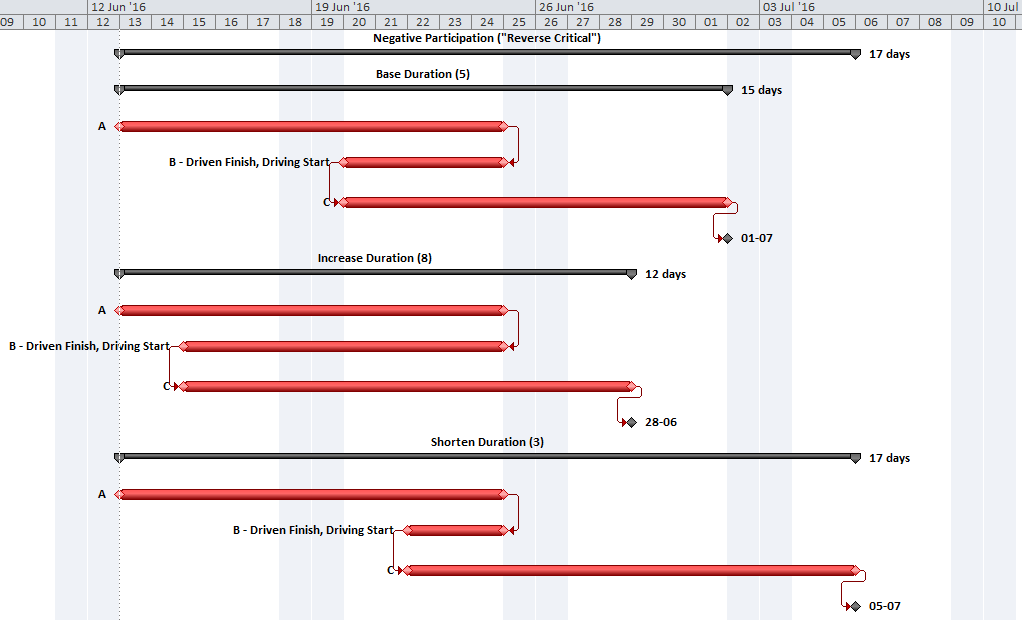
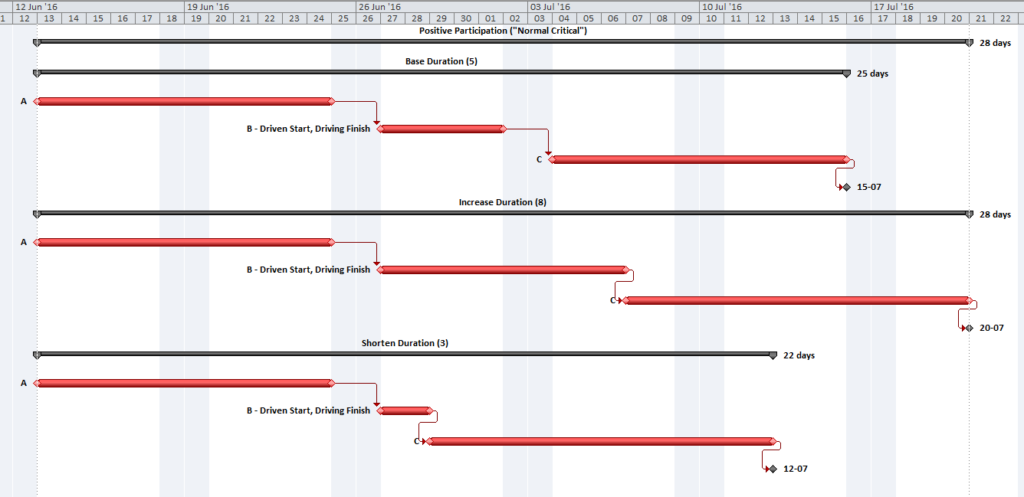
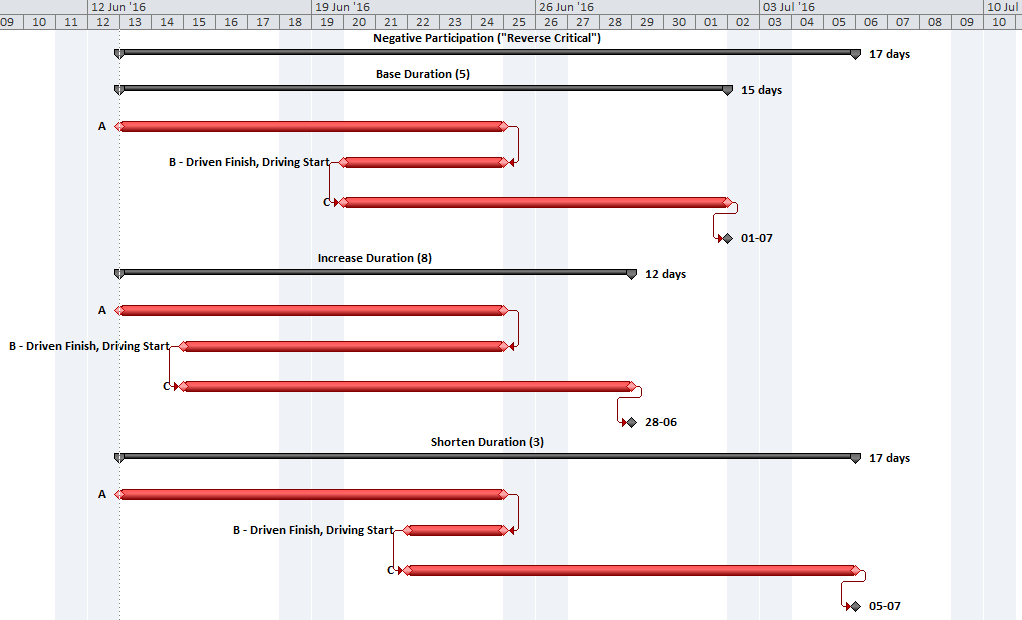
Total Float and its components, Free Float and Interfering Float, are artifacts of the Critical Path Method (CPM) for project scheduling; they are computed and applied for each individual activity in the schedule. Float essentially exists at the activity level, and its aggregation to higher levels of organization (e.g. WBS, Project, Program) is not well established.

In the simplest CPM case (i.e. absent any late constraints, calendar offsets, or resource leveling), Total Float describes the amount of time that a particular activity may be delayed (according to a specific workday calendar) without delaying the overall project. The calculation is made with no concern for risk mitigation, and its result is strictly due to the logic arrangement of activities. Those activities with Total Float=0 are those for which ANY delay will cascade directly to delay of the project – this is the Critical Path. Traditionally, activities with substantial Total Float are allowed to slip as needed to divert resources to the Critical Path. This does not mitigate the overall project schedule risk, however, since the Critical Path itself is not buffered. A distinct schedule contingency/buffer to address schedule risk along the Critical Path is necessary at a minimum. Risk buffering of non-critical activities is also needed to guard against the consumption of float by outside parties. Although contractors will often provide the necessary buffers by padding activity durations, the padding is rarely identified as such (except in NEC contracts). Either explicit schedule contingency activities or explicit identification of risk buffers that are included in activity durations are preferred. Regardless of the method chosen, clearly this is not Float.

Modern CPM schedules often include deadlines or late constraints and multiple activity calendars, and they sometimes include resource leveling. All of these features can substantially affect the computation and interpretation of Total Float, such that it becomes an unreliable indicator of the Critical Path or of any logical path through the schedule. Thus complicated, it is still not useful for risk mitigation.

Finally, because of the float-sharing language that seems common in modern American construction contracts, it is useful to distinguish legitimate schedule buffers (e.g. contingency or TRA) from the vaguely-defined “project float.” That is, where “project float” exists primarily for risk mitigation, one should consider explicitly identifying and scheduling it as a “schedule contingency” (or “reserve” or “buffer”) activity extending from the early project finish to the contractual project finish.

Here is a link to an interesting article from Trauner Consulting on the subject of Shared Float provisions.

http://www.traunerconsulting.com/wp-content/uploads/Manginelli-Shared-Float-Article-FINAL-docx.pdf

Leveling Changes from MSP 2010 to MSP 2013

[I’ve slightly edited this old article – mostly figures. After “upgrading” to Microsoft Project 2016, I can confirm that MSP 2016’s resource leveler appears similar to MSP 2013’s leveler in the simple case examined; both are substantially different from MSP 2010’s.]

Over the last few years, some tests of resource leveling algorithms in various software packages have been reported informally over at Planning Planet.

When using “default” conditions (i.e. without implementing any user-defined priority schemes), the general picture was that leveled schedules from MSP 2010 were significantly longer than those from MSP 2007. There have also been reports that MSP 2013 (and MSP 2016, which seems to use the same leveling rules) produces even longer leveled schedules than MSP 2010. Other software (Spider Project in particular) tend to produce shorter schedules under resource constraints. I haven’t paid too much attention to these reports because a) I don’t use resource leveling often, and b) when I do use leveling, I always define some specific leveling priorities, so the “default” results are not so relevant.

Last week, a French planner (“Alexandre”) on PP noted some significant changes in default leveling results when migrating a simple schedule from MSP 2010 to MSP 2013, wondering what might be the reason for the changes. I’m still on 2010, so I haven’t noticed the change in 2013. While it’s clear that Microsoft has modified the leveling rules from version to version, they don’t publish the details, so addressing the “reason for the change” is just speculation. My own speculation is that minor changes to the leveling algorithm were made to limit apparent changes to the pre-leveling “Critical Path,” even at the expense of extending the schedule. For Alexandre’s specific example:

The project has a total duration of 7.5 days, and the pre-leveling (i.e. CPM) critical path runs through task 5. Task 5 has 0 days of total slack, while task 8 has 2 days of slack.

Leveling Fig0 — Figure 0. Pre-Leveling (CPM) Schedule – 2010

In resolving the resource conflict between task 5 and task 8, MSP 2010’s default rule gives greater scheduling priority to task 5 because:
- The CPM schedule has it starting earlier;
- It has lower total slack in the CPM schedule;
- It has a longer duration;
- It comes first on the task list;
- It is marked as “Critical” (?);
- Some other factors…(?).

(I have no idea what the relative contributions of these factors are in the scoring. Some might be zero.)

- As a consequence of leveling, task 5 (the “critical” one) is scheduled first, while task 8 is delayed, and the project is extended 1 day for a total duration of 8.5 days. Total slack is re-computed after incorporating the leveling delays, and a new “Critical Path” is displayed.
  - Perversely, Task 5 – which was clearly “critical” before leveling and is also clearly a resource driver for the project completion – now has 1 day of Total Slack.
    Figure 1. Leveled Schedule – 2010
  - Task 7 is now shown as “Critical,” even though there is neither a logical nor a resource-driving reason justifying it.
  - So in short, the MSP 2010 leveling algorithm can substantially change the “Critical Path,” and the resulting slack values can be completely misleading. (I wrote about this here: Logic Analysis of Resource-Leveled Schedules (MS Project).)
  - The next figures (from BPC Logic Filter) illustrate the actual resource-constrained Longest Path (Fig. 2) and Multiple Float Paths (2a) through the 2010 schedule.

Leveling Fig2 — Figure 2. Resource-Constrained Longest Path of Leveled Schedule – 2010

Resource-Constrained Multiple-Float Paths of Leveled Schedule - 2010 — Figure 2a. Resource-Constrained Multiple-Float Paths of Leveled Schedule – 2010

In contrast, MSP 2013 task gives greater scheduling priority to task 8, delaying task 5. I suspect this is driven by some complex tuning of the leveling rules around Total Slack.
- Alexandre provided the MSP 2013 leveled schedule here (which also includes a minor date shift).
  Figure 3. Leveled Schedule – 2013
- I’ve repeated it below in my [MSP 2016 model using Standard leveling order.] The resulting “Critical Path” appears essentially the same as the pre-leveling version, but with an added 3-day leveling delay before task 5. This may give project managers confidence that the leveling exercise has not “screwed up” their critical path.
  Figure 4. Leveled Schedule – 2016
  
  Unfortunately, the project finish has been extended by an additional 2 days compared to the MSP 2010 leveler. It is now 10.5 days.

- The project manager’s confidence in the critical path is still misplaced. Task 7 and task 8 are now shown as far from critical, with 5 days of total slack. As shown in the next two figures from BPC Logic Filter, however, they are obviously on the resource-constrained longest path through the schedule.

Figure 5. Resource-Constrained Longest Path of Leveled Schedule – 2016

Figure 5a. Resource-Constrained Multiple-Float Paths of Leveled Schedule – 2016

Comparing the 0-Float Paths of the two schedules (Figures 2a and 5a), we see that unlike MSP 2010, MSP 2013 and MSP 2016’s leveling engine has preserved the logic drivers from the pre-leveling CPM schedule while implicitly inserting task 7 and task 8 into the driving path to project completion. Although the project is extended as a result, the appearance of a stable critical path is preserved. Fortunately, BPC Logic Filter depicts the resulting resource-constrained critical path clearly in both cases.

My speculation on the reason for the changed algorithm is based on the Project development team’s demonstrated preference for the appearance of stability (for mid-level users) over behavior that might be more technically correct from an advanced user’s point of view. (See the handling of inactive tasks in MSP 2013 for another example.)

For an update on this topic, see Resource Leveling Changes from MSP 2010 to MSP 2016 – Revisited

Eddies and Checkdams: Odd Structures in CPM Logic Flow

In logic-driven project schedules, the scheduled start and finish of each activity is determined by a “driving path” of predecessor activities and relationships. Driving logic is said to “flow” along this path from the earliest predecessor to the activity’s completion. In simply-modeled projects, this driving logic flow is one-directional and continuous, such that any delay (or acceleration) of a predecessor task is directly translated to a corresponding delay (or acceleration) of its ultimately driven successors. Thus, delaying a task on the “Critical Path” (the driving path to project completion) ultimately delays the project. More complex schedule models – i.e. those using other than finish-to-start relationship links – allow the driving logic flow to be checked or even reversed, so delay or acceleration of a given task may not have the anticipated result on other tasks or on the project as a whole. Such effects can be transient, appearing and disappearing in the course of a single progress update.

Some Cases

Last year I read a series of articles by Miklos Hajdu (Research Fellow at Budapest University of Technology and Economics) on the sometimes-unexpected consequences of certain relationships in logic-driven project schedules. I encountered them again a few months ago during an extended Linked-In discussion that Hajdu started relating to Drag calculation. (BPC Logic Filter is one of the few scheduling tools that actually sets out to compute drag, and we identified some areas needing standardization of definitions.)

Hajdu’s Articles laid out five basic cases where incrementally delaying or accelerating a particular Critical Path activity might not lead to the expected delay or acceleration of the overall project:

Normal Critical Activities (Expected Behavior – i.e. Lengthening task extends project; Shortening task shortens project.)
Neutral Critical Activities (Neither lengthening nor shortening the task has any impact on project completion.)
Bi-Critical Activities (Either lengthening or shortening the task always extends the project.)
Reverse Critical Activities (Lengthening the task shortens the project; Shortening the task extends the project.)
Increasing Neutral Decreasing Reverse Critical Activities (Lengthening the task has no impact on project completion; Shortening the task extends the project.)
Increasing Normal Decreasing Neutral Critical Activities ( Lengthening the task extends the project; Shortening the task has no impact.)

A more recent blog by consultant Pat Weaver, Critical confusion – when activities on the critical path don’t compute…… reviewed these cases and illustrated the consequences using time-scaled-logic diagrams rather than the simple fragnet blocks first used by Hajdu. With graphical images especially, Weaver has done a great job of clarifying the underlying logic flow and emphasizing the consequences of careless planning. His article is a good read. Unfortunately, his suggestion that competent planners should avoid creating any such constructs in their project schedules seems impractical for planners using P6 or Microsoft Project to schedule complex projects.

I had encountered all of these issues previously in various project schedules and and had focused on them quite a bit while developing the drag-associated parts of BPC Logic Filter – that’s where the “Negative, Positive, and Absolute” terminology below came from.

Driving Logic Flow of the Cases

At the start of a project (i.e. ignoring progress updates and Data Date), every activity is scheduled to be completed according to a path of driving logic (comprising predecessor activities AND relationships) extending from the project start milestone or some valid external constraint forward to the activity’s Finish. (For the particular case of the Project Completion activity, its driving path is synonymous with the “Critical Path” of the project.)

Identifying the “Driving Logic Flow” through any arbitrary activity along that path starts with the Relationship Free Float values of its predecessor and successor links. A Relationship Free Float value of 0 indicates a driving relationship, while a value greater than zero indicates a non-driving relationship.
The activity’s duration “participates” in the driving logic flow if (and only if) there are “Driven” and “Driving” relationships at opposite ends of the activity. Various combinations of relationship float have the implications in the table below.

Relationship Float and Driving Logic Flow

Keeping in mind that any changes to activity duration can immediately change the driving logic flow through the schedule and the associated relationship floats – such that an activity described by the first line of the table above may jump to the third line simply by adding a day to its duration – we can interpret the table as follows:

An activity with a Driven Start and a Driving Finish has a Positive duration participation, as the logic flows forward through the duration from Start to Finish. This is “Normal” in Hajdu’s articles; lengthening the task extends the project, while shortening the task shortens the project. This case seems to represent the vast majority of activities in typical schedules. BPC Logic Filter computes a drag value corresponding to the activity duration, any applicable constraints, and parallel (i.e. near-critical) paths.
Positive Duration Participation in Logic Flow (“Normal Critical”)
An activity with a Driven Finish and a Driving Start, on the other hand, has a Negative duration participation, as the logic flows backward through the duration from Finish to Start. This corresponds to Hajdu’s “Reverse-Critical” case; lengthening the task and thereby allowing it to start sooner ends up shortening the project, while shortening the task and thereby forcing it to start later ends up extending the project. BPC Logic Filter computes a negative drag value for these cases, partly to indicate the apparently perverse logic at work. While such tasks seem to be rare in baseline schedules, I have seen them arise during updating on fairly high-level integrated masters (i.e. not in construction).
Negative/Backward Driving Logic Flow through Duration – Starting Early and working slower Helps; Starting Later and working fast hurts.
For an activity with only a Driven Finish and Driving Finish (or Driven Start and Driving Start), then the duration is bypassed and has no participation in the driving logic flow. This corresponds to Hajdu’s “Neutral Critical” case; neither lengthening nor shortening the task has any impact on project completion, and BPC Logic Filter computes a duration drag of zero for task B. It should be noted that although “dangling starts” and “dangling finishes” are evident in the examples depicted below, they are unrelated to the zero-participation observed. Adding non-driving start predecessors and/or finish successors to Activity B would not change the conclusions.
Logic Flow Duration Bypass – Through Finish

Logic Flow Duration Bypass – Through Start
An activity with both driving and driven relationships at both ends (i.e. minimum Relationship Float = 0 in all four columns of the table) represents four parallel driving logic paths: 1) through the Start only; 2) through the Finish only; 3) forward through the Start, the Duration, and the Finish; and 4) backward through the Finish, the Duration, and the Start. In this case, the Duration Participation is “Absolute,” since any change to the activity duration (either positive or negative) results in positive (lengthening) of the overall path. There is no chance to accelerate the project here, so BPC Logic Filter computes a duration drag of 0. This case corresponds to Hajdu’s “Bi-Critical” case. I’ve added an additional predecessor and successor to the illustration fragnets below – mainly to indicate that its occurrence is not limited to ladder-logic structures. The combined “Positive” and “Negative” behaviors are obvious.
Absolute Participation = Positive/Normal on Lengthening, Negative/Reverse on Shortening
Finally, the four variations of “Limited” Duration Participation arise from the cases where three of the four “Relationship Float” columns are zero. They essentially represent various combinations of “Positive,” “Negative,” and “None” cases above, and they correspond to Hajdu’s “Increasing Normal Decreasing Neutral” and “Increasing Neutral Decreasing Reverse” cases. With any of these cases, it is only possible to Lengthen, never to Shorten, the overall length of the project by modifying the duration of Task B, so BPC Logic Filter computes a drag of zero.
Positive Limited Low Participation – Acceleration won’t help, but slippage will hurt.

Positive Limited Low Participation – Acceleration won’t help, but slippage will hurt.

Negative Limited High Participation – Starting early and working longer won’t help, but delaying start will hurt.

Negative Limited High Participation – Starting on-time and working slower won’t hurt, but starting later and working faster will hurt.

Logic Flow Conclusions

Ultimately, these types of odd logic structures seem to arise from two contributory causes:

The legitimate need for project planners to include in the project schedule no more detail than is necessary to plan and control the work (at the level reflected in the schedule). In Primavera P6 and Microsoft Project scheduling software – based on the precedence diagramming version of the critical path method (i.e. PDM/CPM) – this need is partly satisfied by consolidating many single activities representing simple tasks (with only Finish-to-Start relationships) into longer activities representing more complex work, connected with relationships other than Finish-to-Start. Common examples are Finish-to-Finish and Start-to-Start, often with time or volume lags. As a consequence, driving (controlling) predecessor logic can either “push” an activity (through its “Driven Start”) OR “pull” the activity (by its “Driven Finish”) – or both. Similarly, the activity may drive its logical successors through its “Driving Start” or its “Driving Finish.”
The continuous-activity assumption in the prevailing PDM software packages like P6 and MSP. That is, while the activity may be pushed and/or pulled by predecessor logic, the activity’s duration remains as a rigid connection from Start to Finish, neither stretching nor compressing (nor splitting into parts) in response to logical pressures alone. Consequently, the activity’s duration will be scheduled at the earliest continuous interval that satisfies the most stringent of its start/finish predecessor relationships. All other predecessor relationships will possess “relationship free float.”

Within P6 and MSP schedule models, using Ladder Logic to approximate progressive feeding of work volumes between largely parallel activities is a technique that effectively models the actual work interfaces. Yet it seems virtually guaranteed for such paired-activity ladder structures to encounter at least “neutral-critical” and sometimes “bi-critical” driving logic flow during updating. In my opinion this should be acceptable as long as the paired activities are effectively managed together.

Negative (“Reverse-Critical”) driving logic flow, however, reflects a case where the work being depicted is too complex to be represented by a single activity, and further breakdown is needed. Since it also provides an opportunity for the scheduler to sequester or otherwise manipulate float, the underlying logic structure may be indirectly prohibited by scheduling specifications. BPC Logic Filter presently flags reverse flows of driving logic (using negative drag) during the drag analysis.

The multiple cases where the driving logic flow effectively bypasses an activity’s duration (“Neutral-Critical”) appear to be a natural outcome of the scheduler’s intent. In addition, they seem consistent with the actual work interfaces in some construction projects, particularly where there are substantial variations in the production rates of parallel activities. While BPC Logic Filter doesn’t currently identify such cases, it seems reasonable to modify the Gantt-bar coloring routines in a future release.

Ladder Logic (Parallel SS/FF Relationships) in Microsoft Project

Microsoft Project does not allow users to create multiple logical relationships between the same two tasks. Project DOES ALLOW importing of such multiple relationships in XML files, however. If desired, users can directly edit XML versions of project schedules to introduce multiple logical relationships, and these relationships appear to be persistent and active in all subsequent schedule calculations.

Microsoft Project and Oracle’s Primavera P6 are the two dominant tools for complex project scheduling in North America, and I’ve been a regular user of both tools and their predecessors since the early 1990s. Aside from major issues related to data architecture, one of the key remaining differentiators from a user’s point of view is Project’s limit of one logical relationship between any two pairs of activities.

This limit can be a deal-breaker for longtime users of other tools who are dependent on scheduling workflows using “ladder logic”, or concurrent SS/FF relationships with lag. This kind of logic is used to represent sequentially-related activities whose overall characteristics allow them to proceed mostly in parallel. In construction, a simple example might include digging 1,000 meters of trench, laying 1,000 meters of pipe in the trench, and covering the trench. The most timely and profitable approach to the work is to execute the three tasks in parallel while providing adequate work space between the three crews whose production rates are well matched. Using ladder logic, it is possible to model the work using three relatively long duration activities with concurrent SS and FF relationships. Appropriate time lags are assigned to the relationships to represent the necessary space (or work volume) offsets between the activities. A similar approach can be used to schedule shorter-duration activities performed by successive crews at the same location, where availability of ready work front for the follow-on crew is the the primary constraint. [See also: Overlapping Tasks in Project Schedules.]

In my own experience, I’ve found ladder logic useful for effectively modeling the field approach while avoiding unnecessary detail in the schedule. Implementing ladder logic in Microsoft Project (MSP) requires the use of dummy milestones, complicating the logic and adding needless detail. I would prefer to avoid this workaround. Recently I learned that the one-relationship limit may not be irrevocable, and combined SS/FF links may be used to implement pure ladder logic in MSP (with some outside help.)

Figure 1 illustrates a simple fragnet (in P6) comprising three activities that are linked together with ladder logic. (This is just a test schedule; the implied work relationships are meaningless.)

Figure 1: Typical Ladder Logic in P6 — Figure 1: Typical P6 Ladder Logic with Concurrent SS/FF Relationships and Lags

Figure 2 illustrates the same fragnet (this time in MSP Pro 2010). Dummy milestones have been added to carry the logic through the Start-to-Start side of the ladder, so five activities are needed to schedule the same work that requires only three in P6.

Figure 2: Typical MSP Ladder Logic Using (Dummy) Milestones

Figure 3 demonstrates a fully-functioning MSP fragnet that incorporates dual SS/FF relationships without the aid of dummy milestones. The relationships appear to be fully functioning in the forward-pass and backward-pass calculations, and they are fully editable.* (Like all relationships in MSP, changing the predecessor or successor task requires deletion and re-initiation of the relationship, i.e. not an edit.) It appears, therefore, that multiple relationships between a single pair of tasks does not automatically break the schedule calculations in MSP Pro 2010. Unfortunately, the only way I’ve found to add these relationships is by directly inserting them into an xml version of the schedule file, then opening the file with MSP. (Similarly, P6 schedules that are transferred to MSP through the xml interface can manage to keep their redundant links.) Once opened, MSP appears indifferent to the presence of these externally-inserted dual relationships, but it continues to prohibit introduction of new ones, whether through the standard user interface or through direct manipulation of the underlying data in the open project.

*Interestingly, the only way to successfully edit the dual relationships is using the predecessors or successors list in one of the “task form” lower-pane views as shown here. Attempting to edit using the Predecessors tab of the Task Information dialog window or using the predecessors or successors column in a task table fails — with MSP deleting rather than editing the relationship.

Figure 3: Ladder Logic Loaded Through Edited XML File — Figure 3: Ladder Logic w/ Concurrent Links Loaded Through XML

Overall, I’m encouraged that Project’s longstanding limitation of one relationship per pair of tasks is not – apparently – an inevitable and unavoidable consequence of the program design. Nevertheless, inserting redundant relationships through xml editing hardly seems workable in general, and I doubt that I’ll be using this technique much going forward.

The Resource Critical Path – Logic Analysis of Resource-Leveled Schedules (MS Project), Part 2

BPC Logic Filter for Microsoft Project provides an automated method for extracting and presenting the Resource Critical Path (a.k.a Resource-Constrained Critical Path or Critical Chain) from a leveled schedule.

In a previous entry (Logic Analysis of Resource-Leveled Schedules), I investigated the impact of resource leveling on the logical analysis of Microsoft Project schedules. Conclusions were not encouraging, i.e.:

Project’s Total Slack calculation – and as a consequence, the “Critical” flag – fails to adequately account for resource constraints in the schedule. Neither the “Resource Critical Path” nor any other resource-leveled logical path can be deduced from the schedule by analyzing the logical relationships and slack (nor even the “Leveling Delay” artifacts). Even worse, tasks that are clearly schedule critical when considering resource constraints can have unexpectedly high values for Total Slack and may therefore be neglected during crashing exercises or disruption analysis.
BPC Logic Filter – our preferred tool for logical analysis of Microsoft Project schedules – could not completely overcome the weaknesses of MSP when it came to resource leveling.
To be amenable for logical analysis, it seemed that schedules needed to be constructed with “soft” logic links to mimic the impacts of the resource leveling algorithm.

As the developer and primary user of BPC Logic Filter, I was not satisfied with these latter conclusions. After all, I had developed the tool specifically to overcome MSP’s shortcomings in the context of multiple deadlines/constraints and variable calendars. Why should it stop there?

While I have intended to address resource constraints in BPC Logic Filter since the beginning, I didn’t have much need for it until recently. Now the latest code revision incorporates full analysis and comparison of resource assignments in parallel with the existing logic analysis algorithm. I’m pleased with the results and feel confident that BPC Logic Filter can now depict the Resource Critical Path (or any resource-constrained driving path) in a Microsoft Project Schedule.

Figure 8 of the earlier article showed the resource-leveled schedule of a simple construction project, while Figure 9 showed BPC Logic Filter’s multiple-float-path analysis of the schedule. The latter figure demonstrated how resource leveling introduced gaps into the logical arrangement of the schedule, but it did not track the resource constraints behind those gaps. Figure 11 of the earlier article demonstrated the analysis after replacing the resource-leveling delays with soft (“preferential”) logic links to create exactly the same (early) schedule dates. I’ve included these figures below.

Figure 9: Logic Analysis of Leveled Schedule

Figure 11: Logic Analysis of Schedule with Preferential Logic Instead of Leveling

Now I’ve added a figure (let’s call it Figure 12) showing the “new and improved” analysis from BPC Logic Filter. The top band of the figure illustrates the Resource Constrained Critical Path for the project as originally scheduled and leveled (i.e. without preferential logic). The dates remain unchanged. The relative float values for all tasks are identical to those of the revised (preferential-logic) schedule, but the total slack, critical flag, and bar colors are as originally scheduled and leveled. The next figure (13) shows a revised version of the bar chart with custom bar colors applied to clarify the logic- and resource-driven paths. This is comparable to MSP’s “Task Path” graphical display (though of course that tool is limited to logical paths, does not differentiate among relative float paths, and has no filter.)

Resource Constrained Critical Path from BPC Logic Filter — Figure 12: New Logic Analysis of Leveled Schedule – i.e. Resource Constrained Critical Path

Figure 13 – BPC Logic Filter Bar Colors

To summarize, BPC Logic Filter now includes full analysis of driving resource constraints for leveled schedules.

I’ve tested the upgraded functionality against some of the more sophisticated leveling scenarios, like split-assignments, split-tasks, and in-progress tasks with splits. I’ve also stress-tested the algorithms against some public-domain resource-constrained schedule datasets – namely PSPLIB files j1201_7 and j12060_10, both leveled by MSP with default parameters. For the latter project, BPC Logic Filter required nearly two minutes to chug through the numerous parallel resource-driving paths. (The project includes large pools of homogeneous resources distributed among many small tasks, which I hope is not typical.)

For now, the resource-analysis features do not work across multiple projects (i.e. linked master/sub-project structures.)

Finally, the banner/featured image at the top of this article is an updated version of the project schedule, with a couple arrows added to depict the inherent logic of the resource leveling delays. It would be great for the program to insert these arrows automatically, but I’m afraid the necessary effort isn’t justified at this time. Maybe I’ll revisit in the future.

[See a related video entry here: Video-Using BPC Logic Filter to Analyze Resource Leveled Critical Path]

Find the Connections Between Two Arbitrary Tasks in a CPM Schedule

BPC Logic Filter includes a little feature called Bounded Network (Target Task) Analysis. The feature allows a user to identify all the logical path(s) connecting two arbitrary tasks (or connecting a group of tasks to a single task) in a Microsoft Project schedule. I wrote a few (very dry) pages on it beginning around page 6 of the documentation: Introduction to BPC Logic Filter

I developed this feature out of my own need to efficiently communicate task dependencies to project stakeholders. For example, a piece of major equipment is scheduled to arrive on-site (pre-assembled) on 1April, but it is not scheduled for handover until 1July. For the eventual equipment owner, it is useful to have a graphical depiction of all the tasks – and only those tasks – leading from arrival to handover during the intervening three months (e.g. setting in place, hookups, mechanical inspection, systems testing, commissioning, acceptance testing, endurance testing, training, etc.) While sometimes such tasks all share a common WBS code or custom field, it is rare that such codes correspond 100% with the logical chain(s) of required activities. A logic-based filter provides a clearer picture.

Within the last few days I participated in a LinkedIn discussion on how to develop a similar filter in Primavera (i.e. Oracle Primavera P6), and I’m embarrassed to admit that my initial suggestions (to use Multiple Float Path) were completely wrong. In fact, the quickest way to show the connections between two arbitrary activities is to create a logical loop between them, then try to reschedule the project. P6’s error handler will list all the connecting tasks.

P6 won’t generate the logical filter for you, but the user interface has a very handy feature of being able to add activities to a pre-existing view by simply clicking on the “Goto” buttons in the relationship windows. The list generated by the loop error will guide your selections.

Here’s an example, taken from a ~2000-activity schedule for an ongoing marine project. I have selected two activities whose relationship is not obvious, but which are indeed related.

Figure 1: Filter for 2 Arbitrary Connected Activities

(Using Multiple Float Path analysis of the electrical activity “Connect Paceco…,” I found the plumbing activity “New 4 PW….” activity on float path 168. I didn’t count the activities in float paths 2 through 167, but we need to exclude most of them without examination. MFP is clearly not the answer.)

As shown on Figure 1, I first add a circular successor relationship from the later activity, “Connect Paceco…” to its distant predecessor, “New 4 PW….) Then I try to re-schedule the project. If no error is generated, the two tasks are not related, or the predecessor/successor direction of the connections may be the opposite of what you expect. Figure 2 shows the expected error message, with the listing of the looping paths.

Figure 2: P6 Circular Logic Message (with my cheats)

Now use the list as a guide to attach the connected activities to the existing view.

The result after completing the loop:

Figure 4: Manually Constructed Filter of Path Connecting 2 Arbitrary Activities

You might be tempted to make this into a permanent filter by assigning some custom coding to the visible activities and then making the corresponding filter specification. That doesn’t seem to be worth the extra time to me unless I know for sure that I will be using this filter again. A pdf or screen shot may be all I need.

Many thanks to Khuong Do for raising this question in the Primavera group on LinkedIn. In addition, while the method of manually constructing logical filters by jumping through relationships has been around for many years, I thank Zoltan Palffy and Gail Adams for reminding me that it is still there in P6. Using the circular logic report is something I would never have thought of on my own. All credit to Mr. Gerry Smith in the Primavera LinkedIn group for that stroke of genius.

Just for comparison, I used a laborious process to export this project from P6 to Microsoft Project so that I could run the similar report from BPC Logic Filter. Here’s the result. Yellow and Orange highlighters identify the “Selected” and “Target” tasks respectively. (The P6-to-MSP export/import process is crude: Activity IDs were lost. Calendars were lost, so dates were corrupted. Logic came through with no problems, however.)